浅析高考集合热点
☉河南省巩义二中东校区 王 婧
集合是高中数学中最基本的概念,亦是历年高考必考的知识点之一,常考查集合的基本概念和运算及集合语言和集合思想的应用,考题多为较容易的选择题、填空题.盘点2011年高考试卷中有关集合的问题,认真分析研究,发现考查热点体现在下列六个方面.
一、基本型
这类题型主要考查集合的基本概念和基本运算,常用解法是定义法、列举法、性质法、韦恩图法及语言转化法等.
例1(安徽卷)集合U={1,2,3,4,5,6},S={1,4,5},T={2,3,4},则于( ).
A.{1,4,5,6} B.{1,5}
C.{4} D.{1,2,3,4,5}
解:U={1,2,3,4,5,6},S={1,4,5},T{2,3,4},
评注:本题主要考查集合的交、补运算,因为题设给出的集合是具体的,可采用观察法得到相应的计算结果,也可利用韦恩图辅助求得答案.
二、交汇型
这类题型主要是将集合与不等式、三角函数、解析几何、简易逻辑等知识进行交汇,形成多知识点的综合问题,解题的关键在于灵活运用有关知识.
例2 (湖南卷)设M={1,2},N={a2},则“a=1”是“N⊆M”的( ).
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
解:当a=1时,N={1},满足N⊆M.
反之,若N⊆M,则N={a2}={1}或N={a2}={2},不一定有a=1.
故“a=1”是“N⊆M”的充分不必要条件.故选A.
评注:本题主要考查集合之间的关系,采用充要条件等基础知识,考查学生分析问题和解决问题的能力,属于创新题型.
三、计数型
这类题型是指以集合为背景,求子集的个数、集合中元素的个数等.常用解法是子集的个数公式法、图表法、组合数公式法等.
例3(广东卷)已知集合A={(x,y)|x、y为实数,且x2+y2=1},B={(x,y)|x、y为实数,且y=x},则A∩B的元素个数为().
A.0 B.1 C.2 D.3
解:集合A={(x,y)|x、y为实数,且x2+y2=1}表示圆x2+y2=1上所有点组成的集合,B={(x,y)|x、y为实数,且y=x}表示直线y=x上所有点组成的集合.
故A∩B中有两个元素.故选C.
评注:本题考查集合的表示及集合的基本运算.解题时要注意集合A与集合B中的元素均为点(x,y),A∩B的元素个数即为圆与直线的交点个数.
四、逆向型
逆向型是指已知集合的运算结果,写出集合运算的可能表达式,这类问题往往具有一定的开放性.
A.(-∞,-1]B.[1,+∞)
C.[-1,1]D.(-∞,-1]∪[1,+∞)
解:由P∪M=P,得M⊆P,即a∈P,则a2≤1,故-1≤a≤1.故选C.
评注:本题主要考查集合的运算、简单的二次不等式的解法.
五、判断型
此类问题是判断两个或两个以上集合之间的关系.要正确判断两个集合间的关系,必须对集合的相关概念有深刻的理解,善于抓住代表元素,认清集合的特征,准确地进行转化,通过观察元素的构成结构,借助图形关系寻求集合间的关系,使问题直观准确地得到解决,因此,要重视数形结合思想、转化思想的运用.
例5 (江西卷)若全集U={1,2,3,4,5,6},M={2,3},N={1,4},则集合{5,6}等于( ).
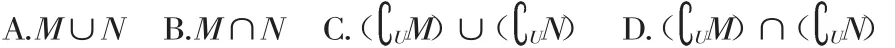
解:由U={1,2,3,4,5,6},M={2,3},N={1,4},得M∪N={1,2,
六、阅读理解型
以集合内容为背景,即时设计一个陌生的问题情景,要求学生在理解的基础上作答.
例6(福建卷)在整数集Z中,被5除所得余数为k的所有整数组成一个“类”,记为[k],即[k]={5n+k|n∈Z},k=0、1、2、3、4.给出如下四个结论:
①2011∈[1];②-3∈[3];③Z=[0]∪[1]∪[2]∪[3]∪[4];④“整数a、b属于同一‘类’”的充要条件是“a-b∈[0]”.
其中,正确结论的个数是( ).
A.1 B.2 C.3 D.4
解:2011=402×5+1,[1]={5n+1|n∈Z},则2011∈[1],故命题①正确.
-3=5×(-1)+2,则-3∈[2],故命题②不正确.
因为所有整数Z除以5可得余数的结果为:0、1、2、3、4,故命题③正确.
若a-b属于同一类,则有a=5n1+k,b=5n2+k,a-b=5(n1-n2)∈[0];反之,若a-b∈[0],也可以得到a-b属于同一类.
有三个命题成立.故选C.
评注:本题是一道比较典型的新定义题,根据给出的定义综合考查了元素与集合之间的关系、集合间的基本运算,同时考查对充要条件的理解.

