新课程下的立体几何教学要做好“三实”

☉江苏省梅村高级中学 吴莉霞

一直以来，立体几何是高中学生数学中必修的一块内容.它对于培养和提高学生的数学能力，尤其是逻辑推理能力和空间想象能力极为重要；同时它在高考中也有着举足轻重的地位.而现在使用的高中数学新教材的内容及其编排上与传统教材相比发生了很大的变化.因此，探讨如何教好这块内容是我们共同关心的课题.下面我结合自己在立体几何部分的教学过程，从以下几个方面谈谈自己对本章内容粗浅的一些体会和认识.

一、教学要突出“实际”

根据《课程标准》的安排，一方面新教材改变了以往传统教材中立体几何的教学顺序，没有从抽象的概念出发，摈弃了以往从局部到整体的教学顺序，而是从学生的直观认知水平这一实际情况出发，遵循从整体到局部、从具体到抽象的原则，先对空间几何体的整体观察入手，再研究组成空间几何体的点、直线、平面的位置关系，从而突出了“直观感知、操作确认、思辨论证、度量计算”等探究性的学习活动，让学生参与到立体几何知识的发生、发展和应用的全过程中来，既学习了立体几何知识，发展了空间观念，又循序渐进地培养了学生的抽象思维与逻辑推理能力.另一方面，新教材中立体几何部分削弱了演绎推理为主要形式的定理证明，减少了定理的数量，删去了大量的几何证明题，淡化了几何证明的技巧，因而在教学时要降低对几何推理证明的要求，不宜挖得过深，不能“穿新鞋走老路”，应该更加注重对学生的几何直观能力、空间想象能力和联系实际应用知识能力的培养.

例如，传统教材中，“三垂线定理及其逆定理”是本部分的核心内容，但新教材有了改变，在江苏省颁布的《高中数学教学要求》中，就明确指出删除“三垂线定理及其逆定理”.同时新课标也没有对这部分内容给出要求，如果讲了这两个定理，学生往往只记住结论，盲目套用定理，这样不利于对空间图形本质的认识，不利于培养学生的学生的“空间想象力”，同时，讲解这部分内容，如果不想费力气，可能教得“半生不熟”，反而产生消极影响.

二、教学要善用“实例”

立体几何与我们生存的现实空间和日常生活联系非常密切，很多实物可以看做空间几何体，而空间几何体中棱与棱、棱与面、面与面之间的关系，实际上就是空间直线、平面的位置关系.教学中，一方面要引导学生从生活实际出发，把所学知识与周围实物联系起来；另一方面，要引导学生经历从现实生活中抽象出空间图形的过程，注重探索空间直线、平面的位置关系，抽象概括它们的判定和性质.

例如，可抓住眼前的实物——笔、纸、桌面、墙面、墙角等正好说明了点、线、面的位置关系，课本的打开与合拢正好是二面角的一个很好的说明.

又如，同学们桌上的念慈庵包装盒、羽毛球包装盒正好是长方体和圆柱体的基本模型，在这些实物的多条边中体现了立体几何中的平行和垂直这两类特殊的位置关系.

其实，新教材中立体几何部分每个几何概念、性质、定理都是由实例导入的，教学中还可以根据实际情况增加实例，让学生经历直观感知、操作确认之后，体验知识发生、发展和应用的过程，培养学生从具体到抽象的抽象能力.

三、教学要强调“实践”

苏霍林斯基说过：“在人的心灵深处，有一个根深蒂固的需要，希望自己是一个发现者、研究者、探索者.”课堂上应多让学生参加实践操作活动，调动学生的多种感官参与教学活动，促使学生主动获取知识.

一方面要鼓励学生自己动手做模型，利用硬纸板作正方体等简单的几何体模型来研究几何体的表面展开与还原，利用牙签搭四面体和正方体等基本模型来研究这些几何体的性质等.

例如，对几何体表面积的教学，笔者以操作实践为主，课前让学生用纸板制作各种柱、锥、台模型.上课时，则让学生把正方体沿着若干条棱剪开后，正方体的各面展开在一个平面内，得到一个多边形，然后观察它们的面积.学生在探究的过程中，用小组合作交流.

另一方面，要让学生充分利用现代信息技术这一有效工具.现如今，信息技术的广泛应用对数学学习、数学教学产生深刻的影响，现代信息技术的图形呈现与制作功能，为立体几何教学提供了得天独厚的优越条件.在教学中，应鼓励学生尽可能使用电脑等数学教育技术平台，运用几何画板、立体几何画板等软件，自己在计算机上制作各种图形，还可以利用动画，把图形旋转、分割、拼接，这样可以解决很多实际模型不能达到的目的.通过计算机图形显示、动画模拟等，形成一个图文并茂、生动直观的教学环境，大大增加教学信息量，提高学习效率，有效地刺激学生的形象思维.

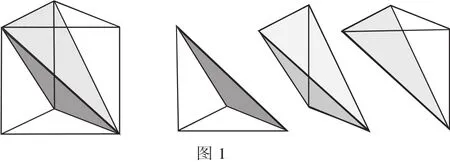
例如，在讲锥体的体积时，可以演示将三棱柱分割成三个体积相等的三棱锥的过程（如图1），既避免了学生空洞的想象而难以理解，又锻炼了学生用分割几何体的方法解决问题的能力.

又如，在用祖暅原理推导球的体积时，运用动画和轨迹功能，当拖动点O时，平行于桌面的平面截球和柱、锥所得截面也相应地变动，直观美丽的画面在学生学得知识的同时，给人以美的感受，创建一个轻松、乐学的氛围.

总之，新的课程标准需要新型的教师.课程改革对我们教师提出了新的要求，教材需要我们去开发、去活用.因此，我们在立体几何的教学过程中，要善用“实例”，同时也要积极调动学生的动手操作能力，通过做模型研究简单几何体的性质.这样一来，学生们从他们的“实践”活动中更加激发了探究、发现新知的欲望和兴趣，在不知不觉中学会了学习立体几何的方法，感受了数学乐趣和数学美，增强了数学思维和数学意识，提升了各方面的数学能力和数学创新.这也正是新教材编者们的初衷.