浅谈2011年高考题中出现的数形结合

☉浙江省诸暨市湄池中学 毛淑萍

数形结合思想是一种很重要的数学思想.数学研究的对象是数量关系和空间形式，即数与形两个方面，把数量关系的研究转化为图形性质的研究，或者把图形性质的研究转化为数量关系的研究，这种解决问题过程中“数”与“形”相互转化的研究策略，就是数形结合的思想.数形结合思想就是要使抽象的数学语言与直观的图形结合起来，使抽象思维与形象思维结合起来.在使用的过程中，由“形”到“数”的转化，往往比较明显，而由“数”到“形”的转化却需要转化的意识，因此，数形结合思想的使用往往偏重于由“数”到“形”的转化.在一维空间，实数与数轴上的点建立一一对应关系；在二维空间，实数对与坐标平面上的点建立一一对应关系.特别是集合、函数、不等式、数列、向量、解析几何、导数与积分等能够用图形表述的知识点，就要用数形结合形象化，高考在选择题、填空题侧重考查数到形的转化，在解答题中，考虑推理论证的严密性，突出形到数的转化.下面谈谈数形结合思想在2011年高考中的体现.

一、利用函数的图像解答问题

例1（陕西理）函数f（x）=-cosx在［0,+∞）内（ ）.

A.没有零点 B.有且仅有一个零点

C.有且仅有两个零点 D.有无穷多个零点

分析：利用数形结合法进行直观判断，或根据函数的性质（值域、单调性等）进行判断.

解： 令f（x）=-cosx=0，则.设函数y=cosx，它们在［0,+∞）上的图像如图1所示，显然两函数的图像的交点有且只有一个，所以函数f（x）=在［0,+∞）内有且仅有一个零点.应选B.

二、利用导数研究图像

例2（浙江文）设函数f（x）=ax2+bx+c（a、b、c∈R），若x=-1为函数f（x）ex的一个极值点，则下列图像不可能为y=f（x）的图像的是（ ）.

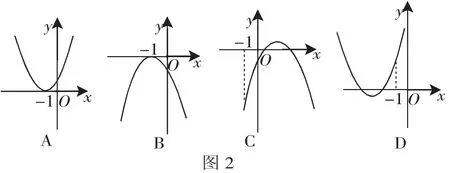
解析：设F（x）=f（x）ex，则F′（x）=exf′（x）+exf（x）=ex（2ax+b+ax2+bx+c）.

由x=-1为f（x）ex的一个极值点，得F′（-1）=e-1（-a+c）=0，即a=c.Δ=b2-4ac=b2-4a2.

当Δ=0时，b=±2a，即对称轴所在直线方程为x=±1；

三、利用不等式表示的平面区域解答问题

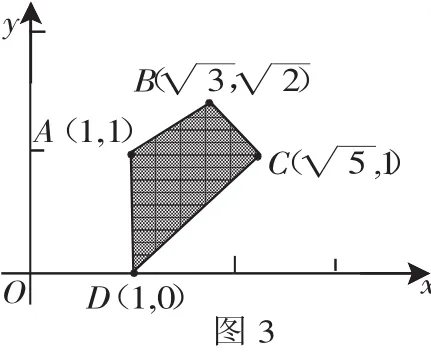
例3 （陕西文）如图3，点（x,y）在四边形ABCD内部和边界上运动，那么2x-y的最小值为________.

分析：本题为线性规划问题，采用数形结合法解答.解答本题的关键是确定目标函数过哪一个点时取得最小值.

解：目标函数z=2x-y，当x=0时，z=-y，所以当y取得最大值时，z的值最小；移动直线2x-y=0，当直线移动到过点A时，y最大，即z的值最小，此时z=2×1-1=1.

四、解析几何问题常常数形结合

例4 （湖北理）将两个顶点在抛物线y2=2px（p＞0）上，另一个顶点是此抛物线焦点的正三角形的个数记为n，则（ ）.

A.n=0 B.n=1 C.n=2 D.n≥3

解析：根据抛物线的对称性，正三角形的两个顶点一定关于x轴对称，且过焦点的两条直线倾斜角分别为30°和150°，这时过焦点的直线与抛物线最多只有两个交点，如图4,正三角形的个数记为n，n=2，所以选C.

五、数形结合在平面向量中的应用也是频频出现

当然，2011年高考中的数形结合问题还有很多，几乎遍及各个知识点，限于篇幅，不再一一举例了.