聚焦高考平面向量题
☉湖南省郴州市湘南中学 曾晓芳
一、近几年平面向量考题的特点
特点一:考小题,重在基础.有关平面向量的小题,其考查的重点在于基础知识:其中,平面向量数量积、加减运算是考查的重点,有关向量共线,向量垂直,向量的模,坐标运算等内容的试题都突出了对平面向量基础知识的考查.
特点二:考大题,与其他知识结合.
有关平面向量的大题,经常与三角、圆锥曲线、函数等结合,与三角函数相结合的试题难度不大,属中档题,与圆锥曲线、函数相结合的试题,属中等偏难,主要考查学生对基本知识,基本方法,基本技能的理解,掌握和应用情况.
特点三:考方法,常体现数形结合的思想方法.
向量的坐标表示实际上就是向量的代数表示.在引入向量的坐标表示后,使向量之间的运算代数化,这样就可以将“形”和“数”紧密地结合在一起.因此,许多平面几何问题中较难解决的问题,都可以转化为大家熟悉的代数运算的论证.也就是把平面几何图形放到适当的坐标系中,赋予几何图形的有关点与平面向量具体的坐标,体现了数形结合的思想.
二、考题聚焦
1.考查向量的概念、向量的基本定理
有关向量概念和向量的基本定理的命题,主要以选择题或填空题为主,考查的难度属中等.
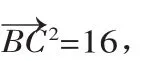

2.考查向量的运算
命题形式主要以选择题、填空题型出现,难度不大,考查重点为模和向量夹角的定义、夹角公式、向量的坐标运算,有时也会与其他内容相结合.
例2 若向量a=(3,m),b=(2,-1),a·b=0,则实数m的值为( ).
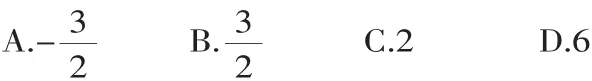
解析:a·b=6-m=0,所以m=6,答案:D.
例3 在平面直角坐标系xOy中,点A(-1,-2),B(2,3),C(-2,-1).
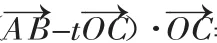
解析:本小题考查平面向量的几何意义、线性运算、数量积,考查运算求解能力.
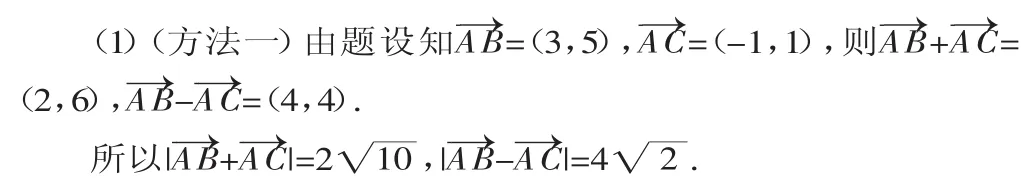
(方法二)设该平行四边形的第四个顶点为D,两条对角线的交点为E,则:E为B、C的中点,E(0,1).又E(0,1)为A、D的中点,所以D的坐标为(1,4).
故所求的两条对角线的长分别为BC=4
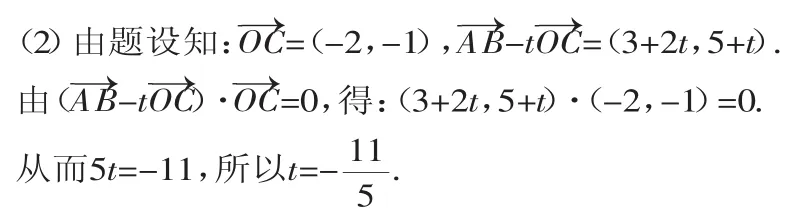
3.向量与三角函数的综合问题
命题以三角函数作为坐标,以向量的坐标运算或向量与解三角形的内容相结合,也有向量与三角函数图像平移结合的问题,属中档偏易题.
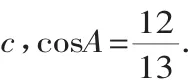
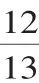
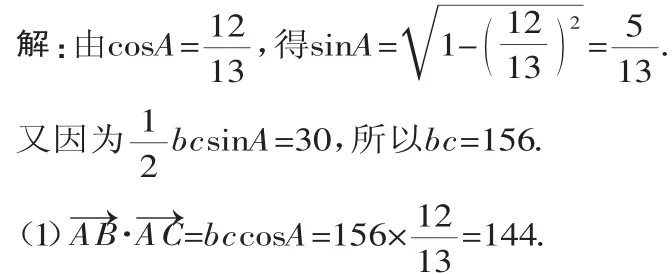
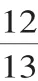
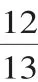
4.平面向量在平面几何中的应用
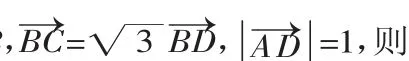

解析:本题主要考查平面向量的基本运算与解三角形的基础知识,属于难题.
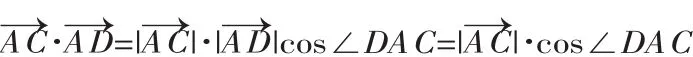

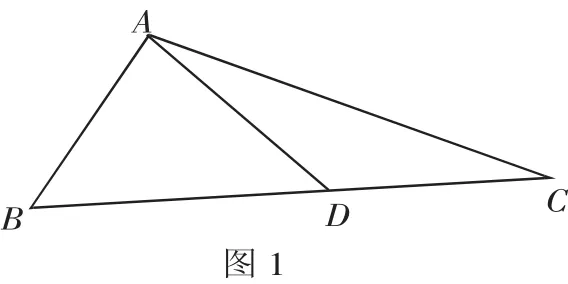
评注:近几年的各地高考卷中总可以看到平面向量在平面几何中的应用的身影,且均属于中等题或难题,应加强平面向量的基本运算的训练,尤其是与三角形综合的问题.
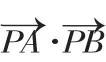

解析1:如图2所示:设PA=PB=x(x>0),∠APO=α,则
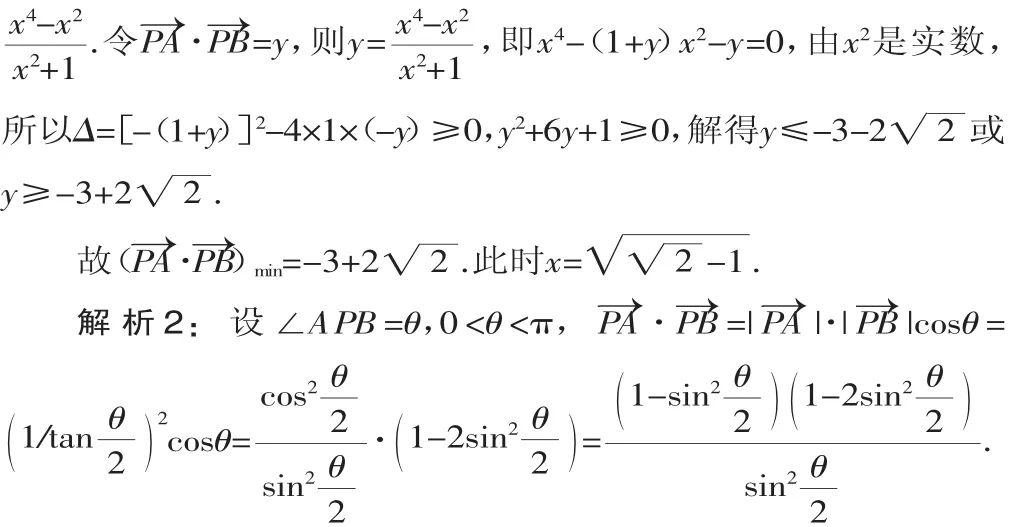
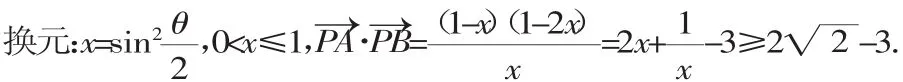
评注:本小题主要考查向量的数量积运算与圆的切线长定理,着重考查最值的求法——判别式法,同时也考查了同学们综合运用数学知识解题的能力.
5.平面向量与解析几何的综合
平面向量与解析几何的综合问题由来已久,多是以解析几何为载体,向量作为条件融入题设条件中.向量与解析几何的结合通常涉及到夹角、平行、垂直、共线、轨迹等问题的处理,其解题策略就是将几何问题坐标化、符号化、数量化,从而将推理转化为运算,沟通点与点之间的坐标关系.三种题型都可涉及.
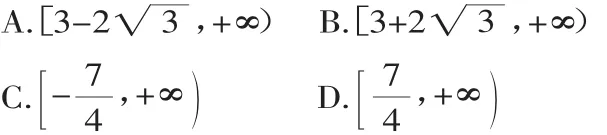
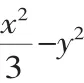

评注:本题考查待定系数法求双曲线方程,考查平面向量的数量积的坐标运算、二次函数的单调性与最值等,考查了同学们对基础知识的熟练程序以及知识的综合应用能力、运算能力.

