运用网络技术 优化教学目标
●白云生 (温州市外国语学校 浙江温州 325000)
教师已对教学目标的重要性有一致看法,认为教学目标是教育目的系统中重要的组成部分,是教育目的、培养目标的具体化,它在方向上对教学活动设计起指导作用,并为教学评价提供依据.教学目标既是教学的出发点,也是归宿,它是教学的灵魂,支配着教学的全过程,并规定教与学的方向.教学目标是教学中师生预期达到学习结果的标准,它既是教师教的目标,也是学生学的目标,也是课程目标的具体化,是在对学生学情、学科特点等方面进行深入研究之后作出的一种理性选择.
传统教学目标的设计主要依据教师对教材的研究和教学经验,教师对教材的研究是设计教学目标的必要工作,但教学经验往往滞后于时代的进步和学生的变化.教师必须更及时地了解学情,使设计的教学目标更适合学生、更适合学生的知识水平、认识能力.利用信息技术和网络技术,教师能够更及时、更全面地了解学情,为设计教学目标提供更好的支持.
1 利用“在线检测”了解学生的预习情况,使教学目标更符合学情
预习是培养学生学习能力非常重要的一个环节.预习既能培养学生独立思考的能力,又能使学生养成良好的学习品质,从真正意义上实现自主、开放的学习.预习有助于清扫学习障碍,搭建新旧知识的桥梁,拉近学生对新知认识的距离,使学生由被动学习变为主动学习.教师的教学目标应在学生预习的基础之上有所调整,应不同于学生没有预习时的教学目标.教师可以利用先进的信息技术和网络技术及时了解学生的预习情况,调整教学目标.笔者通过预习检测题,利用“在线检测”了解学生的预习情况.
案例1 浙教版9年级上册1.1“反比例函数”的教学目标
教材安排共有2个课时,根据所任教班级学生的实际情况,笔者准备将这2个课时合并成1个课时完成.学生能够接受吗?教学目标应该如何设计呢?笔者设计了一份预习检测,测试报告(如图1所示)显示检测平均分达到87%,说明学生通过预习基本掌握了这2个课时的内容.仔细分析测试报告,笔者发现:

图1
(2)由第3题可见,对于2个变量成反比例函数关系的理解不到位,有15%的错误率;
(3)学生对用待定系数法求反比例函数的解析式掌握较好,第7题和第9题的错误率累计只有9%;
(4)学生对实数的运算掌握得不好,如第6题和第8题的错误率较高.
根据以上分析,笔者将这2个课时合并成1个课时,并把教学目标中的知识目标设计为:
通过生活实例体验反比例函数的本质;
理解反比例函数自变量x和比例系数k的取值范围;
会用待定系数法求反比例函数的解析式;
会通过已知自变量求相应反比例函数的值,运用已知反比例函数的值求相应自变量的值.
案例2 浙教版8年级下册1.2“二次根式的性质”的第2课时
这节课的教学内容是二次根式的2个性质:
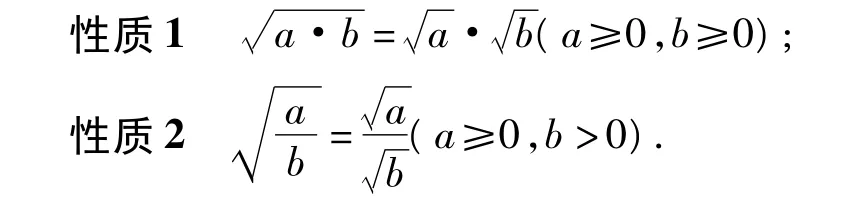
图2

通过以上2个案例不难发现,基于传统经验的教学目标设计可能会偏离学生的学情.通过“在线检测”可以更全面地了解学生的学情,如果能在此基础之上设计教学目标,那么这个教学目标将更有针对性、更符合学生的学情,同时也将使课堂教学过程更高效、更切中要点.
2 利用“班内讨论”了解学生学情,使教学目标更符合学生的学情
网络论坛是人们在网络上进行交流的重要方式之一,教师可以利用论坛给学生一个在线交流、相互讨论的环境.论坛有其独特的优点,比如论坛可以克服课堂教学时间的限制,给学生更平等的交流机会,特别是它给后进生更多的思考时间,给后进生更多的发言机会.笔者利用网站的讨论功能,与学生讨论预习中遇到的问题.
案例3 浙教版8年级下册2.2“一元二次方程的解法”的第1课时
本节课的主要学习内容是用直接开平方法解一元二次方程,用配方法解二次项系数为1的一元二次方程.以下是学生在论坛中发的帖子:
学生1:(1)因式分解法和开平方法可以互换吗?(2)它们之间的关系是什么?因式分解法里包括开平方法,还是其他方法?(3)什么时候用开平方法好,什么时候用因式分解法好?
学生2:完全平方式就是因式分解的一部分,我认为是能用完全平方法解就用完全平方法,否则就用其他方法,如平方差、提取公因式等.
学生3:由开平方法解一元二次方程的基本思路是将方程转化为(x+m)2=n的形式,它的一边是一个完全平方式,另一边是一个常数.当n≥0时,两边开平方便可求出它的根,但为什么要n≥0呢?因为只有非负数才有平方根,所以当n≥0时,方程有解;当n<0时,左边是一个完全平方式,右边是一个负数,因此方程在实数范围内无解.
学生4:解一元二次方程,一般在指明要求用什么方法时,可以先考虑因式分解法.如果是特别形式(x+a)2=b(b≥0),那么可以直接用开平方法.个人认为配方法有点麻烦,最好不要用.总之具体题目,具体分析,用最方便的方法来解.
学生5:一个式子化简后符合x2=a(a≥0)的时候就可以用开平方法,否则就可以用因式分解法.
学生6:像x2+x-1=0这样的方程,怎样才能把常数项改成完全平方要的常数,从而算出方程的解?是不是所有这种类型的题目都应该这样做?还是有其他比较容易懂的方法解这道题?有点糊涂了!
学生7:先把一次项的系数除以2再平方,这就是凑成完全平方的常数项了,再看看原来的常数项差了多少,两边加上差的数就行了.
学生7补充:如果是没有常数项的方程,两边就直接加上差的数就行了.
学生8:解一元二次方程方法归纳:(1)开平方法(最简便的方法,不过很多时候不能直接用);(2)因式分解法(依次考虑提取公因式法、平方公式——平方差公式和完全平方公式、十字相乘法等);(3)公式法(下节课就会学到的,不过个人认为有点难记的);(4)配方法(可以解全部的一元二次方程,但过程最麻烦).
从学生在论坛里发的帖子,笔者发现学生非常关注各种解法的适用题型,而且进行了总结归纳,这些都是学生通过预习自己发现的,教师有必要在课堂中给学生以正确的引导和评价.
因此,笔者认为本节课的能力目标要增加“帮助学生选择适当的方法解一元二次方程”;情感目标应是“体验通过辨析新、旧知识之间的联系提高自己解决问题的能力”.网上讨论还有其他意想不到的好处,它可以把所有网上讨论的内容,无论是错误的开始、失败的终结、或在问题尚未解决前,逐步形成的每个进展,都一一记录下来,把研究的整个过程更全面、更生动、更真实地呈现出来.这些记录可以长久保存,方便师生再次学习.
网络论坛的讨论是“在线检测”的有益补充,教师很难通过选择题的检测发现学生的思维过程和对数学概念的理解,而这些信息对课堂教学特别有意义.教师若能在设计教学目标之前了解学生怎么理解数学概念的,这无疑对教学目标的精确定位非常有帮助.
3 利用“在线检测”了解教学目标的落实情况,为
后续教学目标的制定服务
由于数学知识的内在联系紧密,知识环环相扣,因此制定一节新课的教学目标往往要考虑上一节课教学目标的落实情况.如果上一节的教学目标落实不好,教师应对新课的教学目标作出适当的调整,这样才能使教学目标不脱离学生实际,更有利于章节目标、课程目标的达成.
案例4 浙教版9年级上册1.2“反比例函数的图像和性质”的第2课时
笔者在教授本节课之后,编制了一份课后检测题,从测试报告(如图3所示)中笔者发现第1,3,5,6,7题学生的错误率分别为 15%,20%,17%,20%,35%.可见本节课的教学目标“学会运用反比例函数的增减性解决问题”没有落实到位,这必然会影响下一节课教学内容的展开和教学目标的落实,因此笔者考虑将1.3“反比例函数的应用”的教学目标之一调整为“利用实际问题让学生学会运用反比例函数的增减性解决问题”,通过贴近学生生活的实际问题让学生更好地理解反比例函数的增减性,会用反比例函数的增减性解决实际问题.

图3
利用信息技术和网络技术,教师可以在课后第一时间了解并分析本节课教学目标的落实情况,并及时反思教学行为,调整后续课程的教学目标,更好地进行课堂教学.
总之,教学目标应该是在教学内容与学情分析的基础上形成的.确立教学目标的起点,既要考虑教学内容所提供的“可能起点”,又要兼顾学生的认知水平和认知能力.在教学目标的设计中,教师应充分考虑学生的发展状态,让教学目标的设计更贴近学生的认知水平,使学生学得更轻松,让课堂教学更有效.
[1] 奚定华.数学教学设计[M].上海:华东师范大学出版社,2001.
[2] 潘艺鹏,徐锡健.远程教育中互动教学系统的设计研究[J].数字技术与应用,2009(9):98-100.
[3] 王馨,孟颖.“班班通”引发的课堂教学变革及可持续发展策略探究[J].中国电化教育,2010(9):56-59.
[4] 罗移山.学生:教学的起点——试论灵堂课堂教学目标的设计与实施[J].湖北教育(教育教学),2009(7):28-31.
[5] 阎蔚.教学目标的有效陈述[J].浙江教育学院学报,2002(1):77-81.

