一道中国香港数学奥林匹克几何赛题新证

●陈 宇 (姜堰中等专业学校 江苏姜堰 225500)

第12届中国香港数学奥林匹克试题第3题：

如图1，在 Rt△ABC中，已知∠C=90°，作 CD⊥AB于点D.设O是△BCD外接圆的圆心，在△ACD内有一圆分别与线段AD，AC切于点M，N，并与⊙O 相切.证明：

图1

文献［2］认为：文献［1］提供的参考答案是从证明一个不容易想到的引理出发，然后利用托勒密定理加以解决，实属不易.注意到问题(1)，(2)涉及的线段较多，为此文献［2］依据图形的结构特征，用解析法给出该题的一个另证.

经过一番探究，笔者发现，依据三角及代数计算可以给出该题的一个新证，且思路及计算也颇为简洁.

证明(1)设∠BAC=2α(0°＜ α ＜45°)，BC=2a，圆 Γ1的圆心为 O1，半径为 b.由题设知：∠BAC=∠BCD，AM=AN，OB=OC=a且0＜b＜a.分别联结 OO1，O1N，则

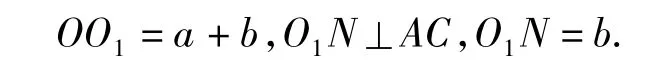
联结AO1并延长交BC于点G，则AG平分∠BAC(易知 CG＜CO＜GB).过点O1作 O1H⊥BC于点H，则

［1］ 中等数学编辑部.2009-2010国内外数学竞赛题及精解［J］.中等数学，2011(增刊)：25-26.

［2］ 彭成.一道中国香港数学奥林匹克几何题的另证［J］.数学通讯，2012(6)：64.