一道中国香港数学奥林匹克几何赛题的三角证法

●王伯龙 (彭阳县第三中学 宁夏彭阳 756500)

题目在Rt△ABC中，已知∠C=90°，作CD⊥AB于点D.设O是△BCD外接圆的圆心.在△ACD内有一圆O1分别与线段AD，AC切于点M，N，并与⊙O相切.证明：

(第12届中国香港数学奥林匹克竞赛试题)

文献［1］提供的参考答案是先证明一个不易想到的引理，然后利用托勒密定理进行解决，思路崎岖，令人费解.其实，虽然所证的结论中涉及的线段较多，但所给的图形比较特殊，因而更容易联想到用解直角三角形的方法证明.

证明如图1，联结OO1，O1N，作 O1E⊥BC，垂足为点 E.设 BC=2R，O1N=r，∠BCD=2θ(R＞r).

(1)在 Rt△BCD中，CD=2Rcos2θ，BD=2Rsin2θ，由∠ACB=90°，CD⊥AB，得

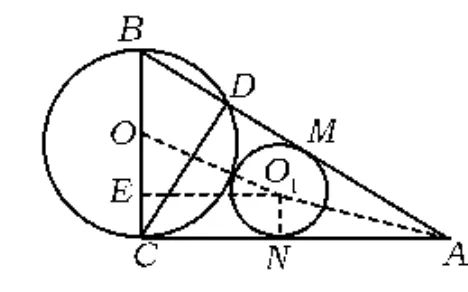
图1

在Rt△ANO1中，由图形的几何性质知，∠NAO1= θ，故 AN=rcotθ，从而化简式(3)，得关于r的一元二次方程

于是又得到如下一个结论：

结论在Rt△ABC中，已知∠C=90°，作CD⊥AB于点D.设O是△BCD外接圆的圆心.在△ACD内有一圆O1分别与线段AD，AC切于点M，N，并与⊙O相切，则

(3)CM平分∠ACD;

(4)DM·AB=AM·BM;

［1］ 中等数学编辑部.2009-2010国内外数学竞赛题及精解［J］.中等数学2011(增刊)：25-26.