一道例题及其变式的设计和初探

●王 云 (浙江师范大学教育硕士 浙江金华 321004)

“几何概型”是人教版高中《数学》(必修3)第3章中的内容.几何概型是一种概率模型，它不同于古典概率，建立几何模型要求随机试验的可能结果是无限的且试验结果在一个区域内均匀分布.随机事件概率的大小与随机事件所在区域的形状、位置无关，只与该区域的大小有关.几何概型把概率问题与几何问题(长度、面积与体积)完美结合，体现了数形结合思想的运用.在实际教学中，如何选择度量刻画所涉及的几何图形是几何概型教学的难点之一.针对这一情况，在几何概型第2课时的教学时，笔者设计了如下例题及其相关探究：

例1 如图1，设M为线段AB的中点，在AB上任取一点C，求3条线段AC，CB，AM能构成三角形的概率.

图1 图2

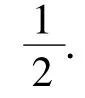
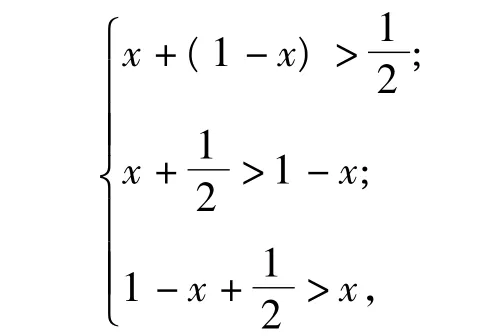
问题1 满足条件的x是有限个，还是无限个?能否用古典概型来解决这个问题?

问题2 几何概型中可用长度、面积、体积来解决问题，对于此问题，大家觉得用什么来解决好呢?为什么?

通过这2个问题引导学生区分几何概型与古典概型，让学生体会如何运用数形结合思想解决问题.此题因只设有一个未知数，可以尝试用一维的几何(即线段的长度)来解决，具体解法如下：

讲授完该例题后，学生对几何概型题有了初步的认识，第3个问题也就随之而来.

问题3 例1中只有一个未知数，在解题过程中用线段长度的比值解决了该问题.设想如果有2个未知数是不是还能用这一方法解决?请大家看探究1.

探究1 将一条长为1 m的绳子，剪2刀后，分成了3段，问恰能构成三角形的概率?

比较例1的解法，可设3条边长分别为x，y，1-x-y.探究1与例1一样也是构成三角形问题，但不同的是，探究1设了2个未知数x，y.设“能构成三角形”为事件B，则样本空间

此时可引导学生用几何概型解题.

问题4 探究1能否用线段长度的比值求解?与例1相比较，有何不同之处?大家能否找到解题的途径?

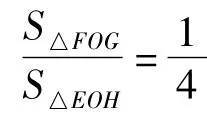
图3

针对数学学有余力的学生可进一步提出如下探究2，尝试从二维面积测度向三维体积测度转变.

探究2 在线段［0，a］上随机地投3个点，试求由原点O到此3点的3条线段能构成一个三角形的概率.

如图4，由题意设组成三角形的3条线段分别为OA=x，OB=y，OC=z，并记“能组成三角形”为事件C，容易得到样本空间

图4

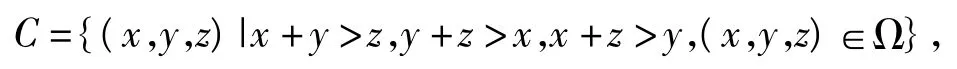
在三维空间Ω中表示边长为a的立方体.同样，事件C要求满足此题的难点是如何正确作出C所表示的空间图形.可先以x+y＞z为例，类比二维平面中y＞x的作图法讲解.

问题5 请学生回忆，在平面直角坐标系中如何作出y＞x的图像?如何确定直线y=x?y=x与y＞x有何区别与联系?

此问题已转变为线性规划问题.不等式的作图可通过等式的作图来实现，即作出区域的边界并验证区域满足不等式.教师要注意引导学生回忆探究中经过两点作一条直线的方法，为解题做好铺垫.

问题6 将二维升至三维，如何作出x+y＞z的图像?它与x+y=z之间是否存在着联系?

问题7 x+y=z是否表示一条直线?如果不是直线，那么它表示什么呢?

问题8 2个点可以确定一条直线，类似地，在空间几个点可以确定一个平面?这些点有没有其他的要求?

设计这一系列的问题，目的是为学生的思考做铺垫，进而引导学生思维的转换，即等式与不等式之间的转换、直线与平面之间的转换、二维与三维之间的转换、面积与体积之间的转换.此间可让学生进行合作讨论，从而得出结论.

不妨设a=1，可通过不共线的3个点A(1，0，1)，O(0，0，0)，B(0，1，1)，先确定平面 x+y=z，即平面AOB;先通过特殊值验证点C(1，1，1)满足不等式，可得不等式x+y＞z表示平面AOB位于点C一侧所在的部分空间(如图5);同理，可依次作出其他2个平面AOD和BOD(如图6).事件C在空间中表示多面体OABCD内部，而样本空间Ω表示为整个立方体，可得

图5 图6

在解题过程中学生对一维或二维比较熟悉，而对三维的空间直角坐标系还不是很了解.在讲解探究2的过程中，根据学生的具体情况可引导学生先降维.样本空间为

Ω ={(x，y，z)|0 ＜x＜a，0 ＜y＜a，0 ＜z＜a}，若把其中的x，y当成是未知数，把z看作为参数，不妨设0＜x＜y＜z＜a，这样一来原本的样本空间可以修改为

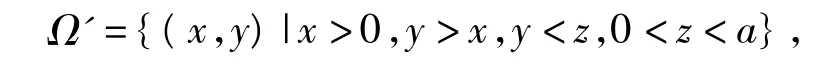
事件C'要求满足

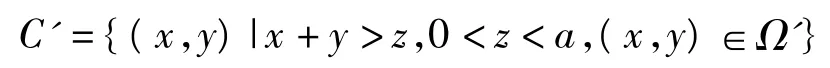
即可，下面可用面积测度解决该问题.

如图 7，Ω'表示三角形OBC的内部，而事件C'中的x+y＞z表示为斜率为 -1、截距为z的直线x+y=z的一侧，并对任意的0＜z＜a成立.经分析可得 C'应为△GBC的内部，可得

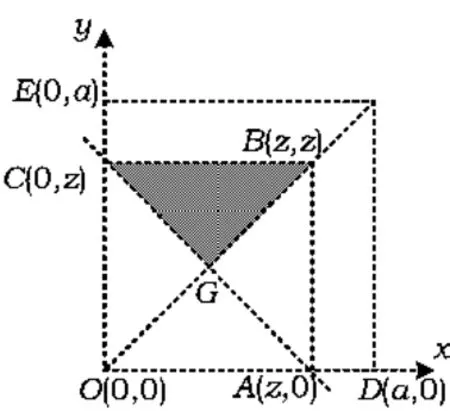
图7

综上所述，从例1、探究1到探究2都涉及到三角形的构成问题，其例题及其变式教学设计旨在引导学生区分古典概型与几何概型.经历建立几何概型问题的数学模型过程，即选择恰当的度量(长度、面积、体积)建立一维、二维和三维几何概型的模型.在课堂教学中，笔者运用了上述设计并渗透类比推理、数形结合和降维等思想方法，取得了较好的教学效果.

以上是笔者在几何概型教学方面所作的一点尝试，期待和同仁探讨，共同提高.