1与0大小比较的探讨

赵立旺 林树杰

（1.重庆经贸职业学院 重庆 黔江 409000；2.奉节县吐祥中学 重庆 奉节 404607）

0 引言

1 预备知识

定义 1[1-2]：对数列｛an｝，若存在常数 a，对于任意 ε＞0，总存在正整数 N，使得当 n＞N 时，|an-a|＜ε 成立，那么称 a是数列｛an｝的极限。 记作

2 结论与证明

（2）证明：

方法一：

设数列｛an｝得首项，a1=0.9，a2=0.99 且满足则：a3=0.999，a4=0.9999……an=0.99…9（n 个 9），由此可构造出

由定义 1 可得：∀ε＞0（ε∈（0，1）），∃N=［-lgε］，当 n＞N 时，|1-an|=10-n＜10lgε=ε，即|1-an|＜ε，故

方法二：

设数列｛an｝为以0.9为首项为公比的等比数列，得a1=0.9，则可构造出

而根据定理1知等比数列｛an｝的和为：

由式（3）和式（4）可得 0.9˙=1，证毕。

方法三：

由式（5）与题设可得 0.9˙=1，证毕。

方法四：

方法五[3]：

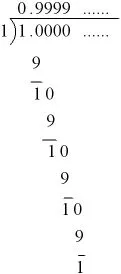
3 结论与反思

［1］朱宝彦,戚中.高等数学[M].北京：北京大学出版社,2007.

［2］史俊贤.高等数学[M].大连.大连理工大学出版社，2005.

［3］http：//topic.csdn.net/u/20080430/13/d6ca2a1d-a6e5-4d15-8361-9c7af5ca616a[J].html?1709972502.