基于双响应面法和BBD 的车辆悬架系统稳健设计
程贤福,袁峻萍,吴志强,槐创锋
(华东交通大学载运工具与装备教育部重点实验室,江西南昌330013)
悬架系统的性能是决定车辆安全性和舒适性的重要因素之一。研究悬架的先进设计理论和技术对车辆的行驶平顺性、操纵稳定性、转向轻便性以及轮胎的使用寿命等有重要意义。在车辆悬架设计中,优化已有较多研究,并且在一定程度上改善了悬架的性能。已有的优化主要集中在以假定设计参数为精确量基础进行的,没有考虑零件的制造误差,因此很难实现可靠优化[1-2]。稳健设计就是要使产品在一些参数值发生微小变动时仍能保证其质量性能指标稳定在允许范围内的一种工程方法。稳健设计方法在设计时就考虑到了制造和使用时的多种不确定因素,能够以低成本的方式保证产品质量,它通过减少可控因素和不可控因素的变差来提高产品的质量[3]13。稳健设计已逐渐在汽车及其零部件设计上得到应用,例如汽车鼓式制动器、转向系统等[4-5]。目前,不少人已将稳健设计方法运用到悬架系统设计当中。例如,车华军等[6]提出基于操纵稳定性的车辆悬架性能参数稳健设计方法;廖林清等[7]以信噪比为评价指标对汽车悬架系统进行了稳健优化等。在现行多种悬架中因麦弗逊悬架比较常见,其结构相对简单,且占用空间较小,是一种典型的独立悬架,由支柱式减震器(减震器和减震弹簧集成在一起)和A字形托臂两个基本部分组成[8],故选用某车辆的麦弗逊悬架作为研究对象。本文在考虑噪声因素即不确定因素的影响下,改变设计变量的取值大小,应用响应面法建立麦弗逊悬架系统的垂直加速度绝对值的双响应面模型,对其系统进行稳健性能分析,获得稳健设计的最终方案。
1 基于响应面法的稳健设计
在车辆悬架系统设计中,正确地运用稳健设计方法,可以使其在经受诸多因素的干扰下,仍能保持性能的稳定。稳健设计的正确运用需要注意以下问题:选出的因素能充分显示对质量设计模型的影响;合理安排试验,注重数值计算,进而获得可靠数据;寻优或寻解。
用响应面法处理稳健设计问题通常由5部分组成,如图1所示。其中最核心的是模拟器C,实际上它是一个数值处理器,将设计变量x、噪声z和一些常因素输入,输出质量特性函数值(所要求的),模型分析中的均值、方差等数值也可以在输出之列[3]188。

图1 响应面法稳健设计的流程图Figure1.Flow chart of robust design based on the response surface method
双响应面法的稳健设计就是根据物理试验或仿真试验的结果,在传统的响应面即仅考虑质量特性的方差σ2基础上增加质量特性的均值 μ,进而拟合出主响应面和次响应面模型[9-10],如式(1)和(2),然后通过两模型进行问题的稳健设计分析。
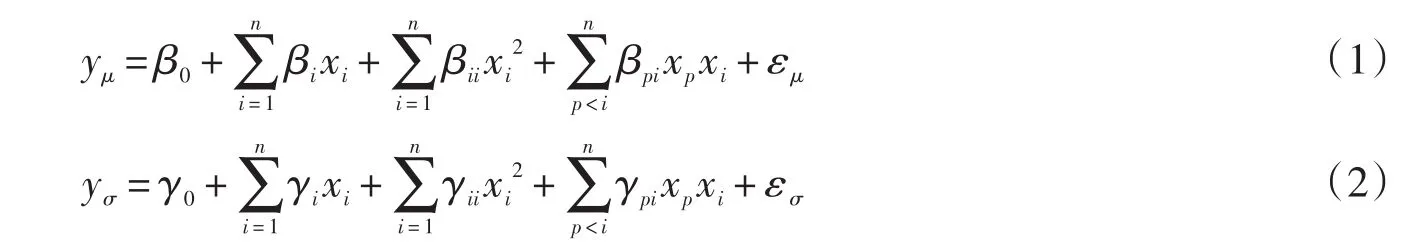
式中:β,γ为响应面系数;ε为近似误差,在满足工程精度要求情况下可近似为0。主响应面和次响应面均为二阶响应面。
2 车辆悬架系统模型的建立
在ADAMS/View中测量悬架的垂直跳动性能,只需建立悬架的简化模型即可。建模过程中对悬架系统进行了以下几个方面的简化:悬架主要由刚体和弹簧构成;忽略其各运动副内的摩擦力;转向拉杆与车架之间的连接简化为球副,下横臂与车架之间的连接采用旋转副,轮胎、转向臂与转向节之间的连接均采用固定副,其他地方的连接均采用球铰副[11]。本文选用某型号车辆的关键点参数,在ADAMS/View中创建麦弗逊悬架系统的简化模型。采用硬点到一般部件,再到几何外形的方式建立悬架的各个组件,然后再用相关的运动副将其连接起来。添加位移驱动为 S=20sin(2πt)[12],其单位为mm。创建麦弗逊悬架垂直运动坐标,并在驱动作用下测量其垂直加速度,进而求得加速度绝对值的均值和方差。如图2所示,建立的部件主要有:1-测试平台、2-轮胎、3-减震器、4-转向横拉杆、5-控制臂(下摆臂)、6-转向节三角臂。
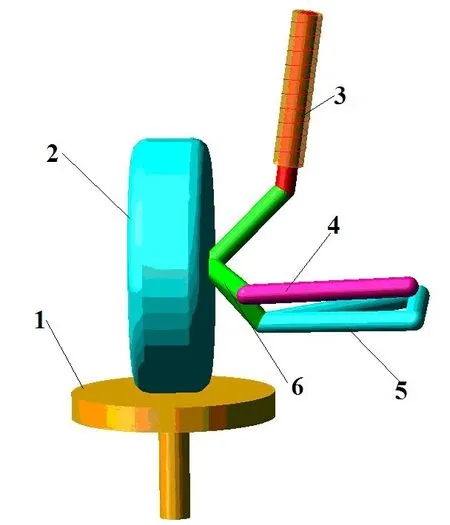
图2 麦弗逊悬架模型Fig.2 McPherson suspension model
3 车辆悬架系统的稳健设计
3.1 设计变量
设计变量即为可控因素,经过一系列仿真分析得到影响该悬架跳动性能较大的关键点,将这些参数作为设计变量,即X=[x1,x2,x3,x4,x5,x6,x7,x8]T;噪声因素即不可控因素。因支柱式减震器是该悬架的关键部件,其结构复杂,但对悬架的整体性能和品质有较大影响。相比可控因素,减震器的弹簧刚度K和阻尼C在加工过程中存在较大随机制造误差,属不可控的,故将其选为噪声因素,即Z=[x9,x10]T。变量名称及其对应物理量如下:x1-下控制臂外球铰点x坐标;x2-下控制臂外球铰点y坐标;x3-下控制臂外球铰点z坐标;x4-下控制臂内后点y坐标;x5-下控制臂内后点z坐标;x6-减震器上端铰点x坐标;x7-减震器上端铰点y坐标;x8-减震器上端铰点z坐标;x9-弹簧刚度;x10-阻尼系数。
3.2 试验设计
因BBD试验方法适合3个及以上的因素,所以可控因素选BBD安排试验,噪声因素选正交试验安排试验。BBD试验设计是用来评价指标和因素间的非线性关系的一种实验设计方法。BBD试验方法的优势:可以评价所有主要影响因子、因子交互作用和纯2次影响项;没有将所有试验因素同时安排为高水平的试验组合,对某些有特别需要或安全要求的试验尤为适用。根据BBD中心组合设计原理,试验以悬架垂直加速度绝对值为响应值,利用De⁃sign Expert软件设计了八因素三水平的响应面试验,共有120组,其中三水平中最大值、最小值各为建模原始数值的±5%。
正交试验设计是应用最为广泛的一种试验设计方法,也是产品质量管理的重要方法之一。它是基于正交表的应用技术,通过合理分析实验的结果,能够很好地提高或改善产品质量。采用正交试验设计方法对影响车辆悬架系统跳动性能的噪声因素进行试验研究,其中三水平中最大值、最小值也各为建模原始数值的±5%。可控因素及水平如表1所示,噪声因素及水平如表2所示。
根据正交助手软件Latin安排正交试验,两因素,三水平,共9次试验。对每组变量进行试验,经过120×9=1 080次试验,得到麦弗逊悬架垂直加速度试验数据。

表1 可控因素Tab.2 Controllable factors mm

表2 不可控因素Tab.3 Uncontrollable factors
3.3 双响应面模型的建立
根据试验的数据进行响应面拟合,得悬架系统垂直加速度绝对值的均值和方差的响应面方程如下:


3.4 试验结果分析
运用软件Design Expert对试验结果进行方差分析,得出各个因素对均值、方差响应的影响。如表3和表4所示。

表3 方差分析(yμ)Tab.3 Analysis of variance(yμ)

表4 方差分析(yσ)Tab.4 Analysis of variance(yσ)
其中,响应面的均值模型中,影响相对不显著的依次是x6,x1;响应面的方差模型中,影响相对不显著的依次是x6,x4,x1,x2,x3,x8。因其它因素P值均小于0.000 1,不区分排序。表中P值为假设机率,是用于判断原始假设是否正确的重要证据。其中P≤0.0001,为高度显著,用**表示;P≤0.05,为显著,用*表示;P>0.05,显著性为不显著。
3.5 稳健设计结果分析
进行双响应面的优化分析,目的就是在保证均值达到或接近目标值的同时,使方差尽可能减小,这就能达到稳健性的设计要求,从而使系统具有良好的质量特征值。根据实验结果及响应面模型的分析,应用双响应面设计方法,以望小特性的优化策略对车辆悬架系统进行稳健设计,获得设计方案,其中目标值F为

式中:λ为加权因子,因为均值和方差两函数值相差较大,故通过线性变换方式将其值控制在[0,1]范围内[14],变换方式如下:

式中∶yTi(x)为目标函数的转换值;yi(x)为实际目标函数值;yimax为取值范围内的目标函数最大值。表5为λ的不同取值所对应的均值、方差、目标值以及双响应面法、传统响应面即单响应面法稳健设计和原始数据三者的对比情况。

表5 设计结果Tab.5 Design results
由表5可知,运用响应面法对悬架系统进行稳健设计,结果显著。单响应面法是仅建立产品质量特性方差的响应面模型,以产品质量特性方差最小为目标,对车辆悬架系统进行设计。可以看出,和单响应面法相比,同时建立质量均值和方差的双响应面法,其得到的垂直加速度的均值,因λ取值不同,其值部分比单响应面法小,而方差的取值则稍微偏大。说明按照该目标,运用双响应面法进行的车辆悬架稳健设计,若因素在一定范围内波动,则系统具有一定的稳健性,但该解不是最优的。运用ADAMS软件将λ取某值时的悬架垂直加速度曲线和原始曲线绘制如图2所示。
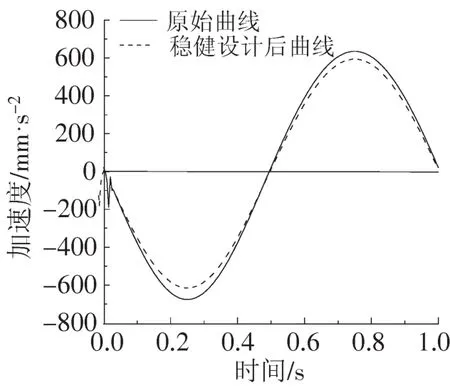
图2 设计结果曲线图Fig.2 Curves of design results
4 总结
1)通过试验结果对比,发现双响应面法相对传统的响应面法虽然优化效果不是很明显,但对稳健设计很有效,运用ADAMS软件对试验结论进行仿真,结果与理论设计相一致,且稳健设计效果明显;
2)运用双响应面和BBD试验法建立车辆悬架系统的双响应面稳健设计模型,不仅可以使设计解在所选的可控因素或不可控因素干扰下仍能保证设计目标波动的极小化,并且能够保证目标趋于最优;
3)这种方法具有通用性,可以应用到其它类型的车辆悬架中。运用这种方法指导实际生产,在制造过程中可以适当放宽不显著因素的精度,保证显著因素的精度,这样既能保证质量又节省成本。
[1]吕彭民,和丽梅,尤晋闽.基于舒适性和轮胎动载的车辆悬架参数优化[J].中国公路学报,2007,20(1):112-115.
[2]王涛,陶薇.考虑随机因素的汽车悬架参数多目标稳健优化[J].振动与冲击,2009,28(11):146-149.
[3]陈立周.稳健设计[M].北京:机械工业出版社,1999:13-188.
[4]程贤福,熊坚,李骏.汽车鼓式制动器的可靠性稳健优化设计[J].华东交通大学学报,2009,26(2):67-71.
[5]CHENG XIANFU,ZHANG XIN.The robust reliability optimization of steering mechanism for trucks based on non-probabilistic interval model[J].Key Engineering Materials,2011,467-469:296-299.
[6]车华军,陈南,殷国栋.基于操纵稳定性的车辆悬架性能参数稳健设计方法[J].汽车工程,2009,31(4):371-375.
[7]廖林清,刘鑫.汽车悬架系统参数的稳健优化设计[J].重庆工业管理学院学报,1995,9(4):49-53.
[8]诸葛晓宇.基于CATIA/ADAMS的麦弗逊悬架运动分析[J].汽车零部件,2011(9):61-64.
[9] DING LIN D K J,WEI D.Dual-response surface optimization:Aweight-ed MSE approach[J].Quality Engineering,2004,16(3):31-39.
[10]LIU YUQIANG,CUI ZHENSHAN,ZHANG DONGJUAN.Six sigma optimization in sheet metal forming based on dual response surface model[J].Chines Journal of Mechanical Engineering,2006,19(2):251-255.
[11] KIM C,RO P I,KIM H.Effect of the suspension structure on equivalent suspension parameters[J].International Journal of Vehicle Design,1999,213(5):457-470.
[12]邵昭晖.汽车麦弗逊悬架三维设计与运动分析[D].武汉:武汉理工大学,2011:27-28.
[13]赵秀婷,张文明,申焱华,等.基于偏好聚合不精确法的湿式制动器稳健设计[J].机械设计与研究,2007,3(1):22-25.
[14]SUN QIHAN,DONG ENGUO,ZHANG LEI.Helical spring design based on dual response surface[J].Journal of Liaoning Technical University,2011,30(1):81-84.

