基于matlab/simulink 的车辆建模与故障分析
颜 秋,刘永明
(同济大学铁道与城市轨道交通研究院,上海201804)
随着铁路行业高速发展,列车运行速度逐渐提高,铁路安全越来越受到人们的重视,如何保证铁道车辆运行安全及其故障监测成为一个亟待解决的重大课题。客车车辆在结构上的故障主要有一系弹簧断裂、减振器失效、空气弹簧漏气、高圆弹簧断裂、车轮踏面擦伤、轴承故障以及蛇形减震器故障等等[1],各种故障对车辆运行品质有不同程度的影响,严重情况下可能会威胁到车辆的安全运行。因此,对车辆故障的监测与识别成为了保证车辆安全运行中必不可少的措施。目前,对铁道车辆的故障监测主要有地面和车载两种形式,其中在车载监测系统中,使用振动加速度传感器监测车辆运行状态较为普遍,以此可以迅速实现检测信号的分散收集、处理及故障判别[2]。
对于利用振动加速度响应进行监测的系统,信号可能会受到多方面的影响,如轨道随机不平顺激励的干扰、车辆本身非线性对信号传递的干扰以及各种故障叠加后对检测信号的干扰等等。文章中仅建立整车线性动力学模型,不考虑轮轨蠕滑等非线性因素对信号的影响,主要讨论不同位垂向悬挂故障时,振动加速度信号具有的统计特性规律以及影响数字特征的因素。
1 建立车辆模型
由于matlab/simulink软件可以使用面向对象的框图建模[3],同时具备子系统封装的特点,对于含有弹簧阻尼的线性系统,可以拆分为悬挂子系统和刚体状态子系统,按刚体间不同的连接形式,快速建立系统线性模型。以简化的车辆二自由度系统为例[4],其运动微分方程:式中:Fk1=K1(Z0-Z1);Fc1=C1(̇0-̇1);Fk2=K2(Z1-Z2);Fc2=C2(̇1-̇2);Zi(i=0,1,2)分别为车轮、m1和 m2离平衡位置的位移。

与m1相连接的弹簧阻尼分别为K2,C2,K1,C1,在任意时刻t,车轮、m1,m2运动状态不同,在相互作用下会产生Fk1,Fc1,Fk2,Fc24个弹簧阻尼力作用在m1上,将4个弹簧阻尼力作为m1受力输入端口,̈1作为状态输出端口。同理对于m2,Fk2,Fc2作为受力输入端口,̈2作为状态输出端口。因此对于m1,m2状态子系统,其输入为弹簧阻尼力,输出为刚体运动状态,对于悬挂子系统Fk1,Fc1,Fk2,Fc2,其输入为悬挂两端刚体的运动状态,输出为弹簧阻尼力。
以上述方法为基础建立车辆的simulink框图模型,模型以目前应用较多的无摇枕四轴客车为例,自由度分别是车体和前后转向架沉浮、横移、点头、侧滚及摇头,以及车轮沉浮、横移、侧滚及摇头,共31个自由度,其中将一、二系悬挂作为悬挂子系统,将转向架和车体作为刚体状态子系统,建模时忽略了轮轨蠕滑和车轮侧滚引起的横向力变化。
2 车辆悬挂的故障分析
2.1 一、二系悬挂故障形式及统计特性
主要讨论车辆垂向一、二系悬挂故障形式,尤其是单一悬挂故障,将前转向架前轴左侧一系悬挂记为一系11位悬挂,右侧为一系12位悬挂,其余类推。在模型中对故障的检测是通过车辆振动加速度信号来实现,测量点位于前后转向架和车体中心。由于车辆正常运行和悬挂故障时振动响应信号不同,经过时域和频域分析,提取出信号的统计特性,并计算出相应的数字特征,以此判别车辆运行中是否出现故障。在时域分析中,信号的统计特性主要用3个典型的数字特征来描述,分别是均值αˉ(t)、方差S2(t)和均方根值φα(t)。在频域分析中,主要使用加速度功率谱密度Pα[5],其数字特征是局部频率段上的均方根值φα(f)。
仿真中,以车体和前转向架为例,一系悬挂故障用刚度增大10倍[6],阻尼为0模拟,二系悬挂故障用刚度增大20倍,阻尼为0模拟。加速度检测信号采样频率为1 000 Hz,运行时间为10 s,车速为定速80 km·h-1,在直线轨道上行驶,用matlab自带pwelch函数进行功率谱分析。时域上,车辆振动加速度数字特征见表1,从中可以观察到,车辆正常运行与故障时,f1(t)与b(t)变化规律并不明显。当一系故障后,S2(t)和φα(t)均呈现增大趋势,尤其是(t)增大明显,易于识别,当二系故障后,(t)和 φαf1(t)减少,而车体增大,由此说明,二系悬挂故障抑制了转向架振动加速度波动幅值。

表1 时域上振动加速度数字特征Tab.1 Digital characteristics of vibrating acceleration in the time domain
频域上,加速度功率谱Pα采用半对数曲线,如图1和3,从中可以观察到,车辆正常运行时,1转向架与车体主要振动能量峰值主要集中在0~18 Hz之间,1转向架加速度功率谱值Pαf1在10-5~10-1之间,峰值位于4,8,14 Hz和16 Hz左右,车体加速度功率谱值 Pαb在10-7~10-2之间,峰值位于1.5,4,8,14 Hz和16 Hz左右。当一系故障后,Pαf1峰值明显向高频处移动,分布在13~17 Hz之间,车体在低频0~2 Hz处Pαb峰值减少,而在8 Hz处峰值增大,能量向10~20 Hz高频段移动。这是由于一系悬挂故障后,一系刚度明显增大,减振器失效,高频振动更容易经转向架传到车体,使转向架和车体振动能量趋向高频。
当二系故障后,在4 Hz和8 Hz左右,Pαf1峰值明显减少,部分向低频0~2 Hz集中,部分向高频10~20 Hz移动,这是由于二系悬挂故障后抑制了1转向架3~10 Hz上的振动能量,其结果与时域分析相同。对车体而言,Pαb并未明显向高频移动,而是在低频0~4 Hz处增大。此外,在一、二系悬挂故障后,车辆在20~100 Hz内Pα比正常时也有不同程度的增大。
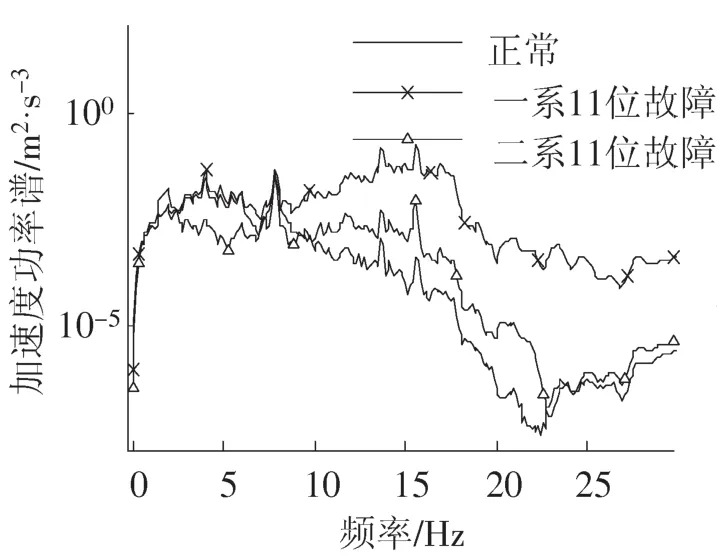
图1 1转向架加速度功率谱Pαf1Fig.1 The power spectrum of bogie acceleration
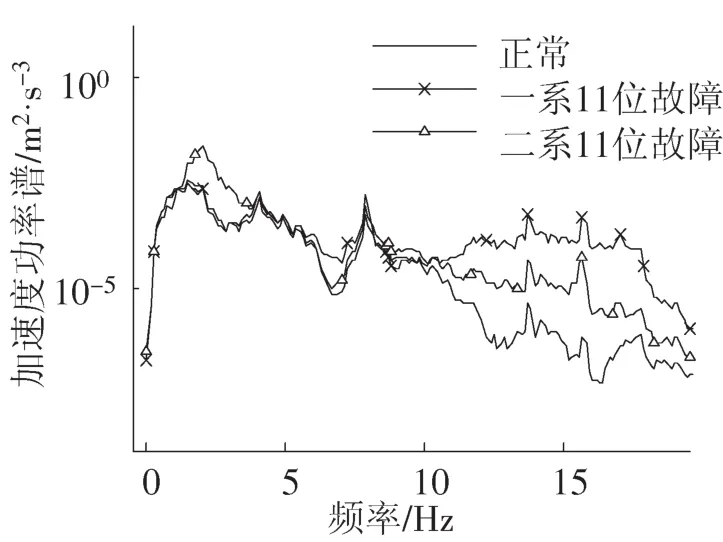
图2 车体加速度功率谱PαbFig.2 The power spectrum of body acceleration
综合上述讨论,时域上可用于故障判别的数字特征主要是S2(t)与φα(t),αˉ(t)由于变化不明显,仅作为辅助参考。在频域上,由于故障前后Pα峰值变化主要集中在0~20 Hz的频率内,在20~100 Hz内功率谱值也有明显变化,但其值相对较小不利于识别,仅作为辅助参考。因此,用于故障判别的数字特征采用0~20 Hz内主要峰值对应频率段上的均方根值φα(f),余下峰值频率段以及20~100 Hz内的φα(f)作为辅助参考。以1转向架为例,在一系11位悬挂故障后,主要振动能量峰值对应的频率段及其数字特征见表2,从表中看出,与正常相比,故障后频域上的数字特征非常易于识别,尤其在后3个频段上的变化最为明显。对于车体,则应加上0~2.2 Hz的低频段,同理在二系悬挂故障后也采用相同方法,只是提取的频率范围有所变化。

表2 一系11位悬挂故障后频域上数字特征Tab.2 Digital characteristics in the frequency domain after 11 suspension failure
2.2 数字特征的影响因素
由于通过车辆振动加速度响应信号来判别车辆运行状态是十分复杂的问题,在振动信号中可能会掺杂许多干扰信号,影响到识别故障的数字特征,因此有必要对可能出现的影响因素进行讨论,防止故障误判。
1)不同位悬挂故障叠加对振动检测信号干扰较大,但在实际运行中,多悬挂故障并不常见,文中仅讨论两位悬挂的故障叠加。在时域上,当一系11,21位单侧故障后,(t)为0.260 9,小于单一11位悬挂故障。当11,22位对角故障后,(t)为1.005 2,明显大于单一悬挂故障。在频域上,当1系11,21单侧故障后,如图4和图5,转向架与车体在13~17Hz内振动能量峰值比单一11位故障明显减少,其中在15.4~16 Hz内,φαf1(f)减少0.0623,φαb(f)减少1.90×10-4。而一系11、22对角故障时,13~17 Hz内峰值明显增大,其中在15.4~16 Hz内,φαf1(f)增大0.1366,φαb(f)增大 4.11×10-4。此外,对一系11、42位对角悬挂故障仿真发现,φαf1(f)与一系11位单一故障时完全相同,说明后转向架悬挂故障对前转向架信号影响可以忽略不计。而车体在3~8.1 Hz频率段内峰值减少,在3.8~4.2 Hz内,φαb(f)比单一悬挂故障时减少5.15×10-4,在7.6~8.1 Hz内,φαb(f)减少3.13×10-4,余下辅助频率段4.2~7.6 Hz内,φαb(f)减少 7.13×10-4。
由此可见,一系不同位悬挂叠加后,由于自身结构与轨道激励不同,与单一悬挂故障相比,数字特征并未呈现相同的变化规律。当频域上局部频段的数字特征明显小于单一悬挂故障的临界值时,则应结合其余峰值对应频率段、辅助参考频段和时域的数字特征联合判别悬挂是否故障。而对于大于单一悬挂故障临界值的情形,则有利于故障判别。
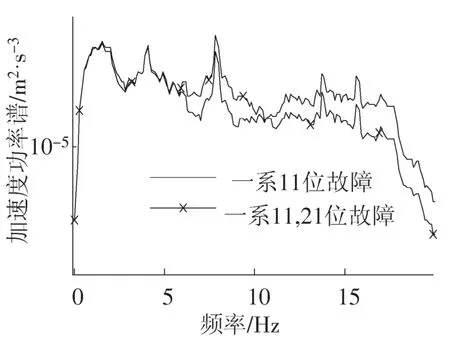
图3 1转向架加速度功率谱Paf1Fig.3 The power spectrum of bogie acceleration
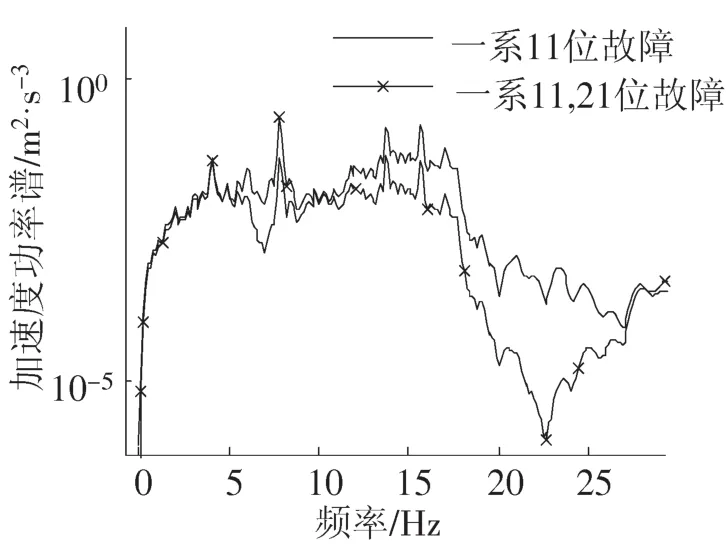
图4 车体加速度功率谱PabFig.4 The power spectrum of body acceleration
2)轨道随机不平顺对车辆运行平稳性影响较大,尤其是当轨道中存在短波和中波不平顺[7-8]时,会使车辆垂向振动加速度增大。仿真中,添加的短波不平顺是三角坑高低不平顺,连续三波组合,波长为2.4 m,波幅为12 mm,时域上对应的频率为9.25 Hz。中波不平顺是连续三波高低不平顺,波长为15 m,幅值为12 mm,时域上对应的频率为1.481 5 Hz,二者分别存在于左轨道激励中。仿真结果以1转向架为例,如图6,短波三角坑不平顺使1转向架在7~10Hz频率段中 φαf1(f)比正常时增大5.70×10-3,其余频率段影响微小。中波三波不平顺对1转向架0~20 Hz内数字特征值影响较小,20~100 Hz的辅助参考频段上φαf1(f)增大2.60×10-6。此外,从车体响应中发现,三角坑不平顺使车体在7~10Hz内 φαb(f)比正常时增大1×10-4,三波不平顺使车体在0~2.2 Hz内 φαb(f)比正常增大 4×10-4。
由此可见,轨道随机不平顺波长不同,对车辆振动影响不同。短波对转向架影响较大,中波主要影响车体低频振动,二者影响主要集中在波长对应频率段附近,使得局部频率段上的数字特征产生波动,而对其余频率段影响微小。
3)当列车正常运行速度为120 km·h-1时,采样频率保持不变,时域上,1转向架检测的φαf1(t)增大到0.443 1,与一系悬挂故障的数字特征接近。在频域上如图5,转向架加速度功率谱最大峰值增大,全部峰值均向高频移动,这是由于车速提高后,车辆振动加剧,振动能量趋向高频[9],同时固定的采样频率使得仿真结果误差进一步增大。因此,检测时应保持前后车速一致,否则会影响到信号的数字特征。
2.3 故障的判别
对于车辆故障的判别,采用频域为主、时域为辅多位置联合判别的方法,在频域上,求出车辆正常运行和一、二悬挂故障时车体和前后转向架在各自频率段上的数字特征,将其作为参考数据存于数据库中,同理在时域上也建立正常和故障时的统计特性数据库。当获得故障检测信号后,首先在频域上与正常运行参考数据对比,查看其是否超过临界值,以此判断其是否属于故障信号,然后将车体、前后转向架三位置数字特征与数据库中数据分别对比,并结合时域数字特征,判断其属于一系还是二系故障。当检测数据与参考数据部分匹配时,则需利用辅助参考频段上的数字特征,进一步确认是否为故障叠加或轨道不平顺激励等等因素的影响,最终确定车辆悬挂是否故障。
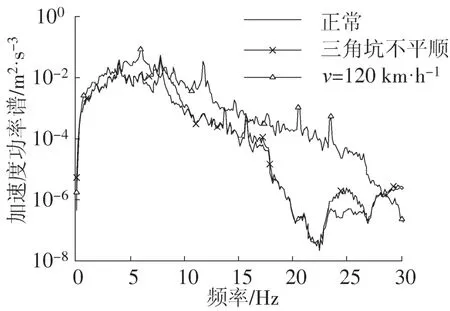
图5 1转向架加速度功率谱Pαf1Fig.5 The power spectrum of bogie acceleration
3 结论
以simulink框图建模的方法搭建车辆线性模型,将复杂车辆模型拆分为悬挂子系统和刚体子系统,使得模型结构清晰直观,同时通过调节不同参数实现不同形式悬挂故障的模拟仿真。利用振动加速度信号在时域和频域上分析,可以得到车辆故障的统计特性,将检测信号与此对比即可判别车辆悬挂工作状态。不同位故障叠加、轨道随机不平顺和运行车速对悬挂故障的数字特征有一定影响,但结合多频段及时域的数字特征分析,仍可消除对故障判别的影响。而对于轮轨擦伤、止档贴靠等非线性因素仍需进一步讨论。文中对于故障的判别方法仅提出了初步的建议,对于有效可靠的故障判别模式和不同位悬挂故障的准确区分与定位仍需要今后深入研究。
[1]郭秀玲,吕青峰.客车振动故障的初步分析[J].铁道机车车辆工人,2002,9(9):10-12.
[2]张兵.列车关键部件安全监测理论与分析研究[D].成都:西南交通大学,2007:9-70.
[3]沈钢.面向对象的机车车辆动力学仿真建模研究[J].铁道学报,1998,20(2):1-6.
[4]胡用生.现代轨道车辆动力学[M].北京:中国铁道出版社,2009:20-60.
[5]李海涛,王成国.基于轨道车辆频域模型的二系垂向悬挂元件状态监测[J].铁道机车车辆,2008,28(2):1-5.
[6]杨蔚原.Welch功率谱估计方法的参数选择[J].环境技术,2009,27(5):23-27.
[7]练松良,黄俊飞.客货共运线路轨道不平顺不利波长的分析研究[J].铁道学报,2004,26(2):111-115.
[8]李再帏,练松良,李秋玲,等.城市轨道交通轨道不平顺谱分析[J].华东交通大学学报,2011,28(5):83-87.
[9]于卫东,曾宇清.车辆安全监测装置仿真测试的随机试验分析与评判原则[J].铁道机车车辆.,2003,19(1):46-49.

