AT 供电牵引网故障测距仿真研究
杨丰萍,王喜燕
(华东交通大学电气与电子工程学院,江西南昌330013)
接触网故障的精确定位对缩短抢修时间、提高运输效率将具有直接的影响。由于在输电线路方面行波故障测距的研究已经成功应用,因此接触网的行波测距也成为了人们研究的热点。文献[1]对牵引网的T-R+NF供电电方式和AT供电方式下分别综合A,C两种测距方法进行了仿真研究,它们都是单端测距法,需要检测从故障点反射回来的行波,但是牵引网远比一般的供电线路复杂的多。如众多的分支站场、频繁的锚段电联结、电力机车的运行等使得牵引供电线路的结构更加复杂,导致行波的折射、反射以及透射相互干扰[2-3],极大的增加了获取有效故障行波的难度。但是D型行波测距法只需要获取故障点向两端传播的初始行波波头和故障点返回来的反射波,并且受线路及机车状况的影响较小。当牵引网中存在分支站场时行波会在分支点产生反射并与故障点的反射波混在一起不易区分,在这种情况下基于检测故障点反射波的单端测距法就不适用了,因此本文采用基于双端的D型测距法很好地解决了这个问题。
1 D型测距法原理
作为双端测距原理的D型行波故障测距法利用了线路内部故障产生的初始行波波头到达线路两端检测点的时间之差来计算故障点到保护安装处之间的距离[4]。由于不需要检测反射行波,因此其更适用于多分支站场和频繁的锚段电联结的接触网行波故障测距,如图1所示。图中B为变电所的母线。
故障初始行波波头从故障点向两端母线传播的所需要的时间分别为Tm和Tn,由图我们可以得到下式


图1 D型行波测距原理示意图Fig.1 Schematic diagram of D-type traveling wave ranging principle
式中:DmF和DnF分别为m端和n端母线到故障点的距离;L为线路mn的长度;v为行波传播速。由上可知,只有故障发生在mn之间时此法才有效。通过上式可以得到m端和n端到故障点的距离

D型现代行波测距原理对两端母线的时钟要求非常高,它们必须保持同步。而现代GPS技术的应用使两端的时钟的精确度大大提高,时钟的时间同步误差平均不超过1 μs,极大的提高了测距的精确度。此种测距方法还需要判定是否为区内故障[5]。在线路任一端通过比较由故障初始行波波头所引起本端电压和电流暂态分量的极性可以有效地识别出是线路正方向故障还是反向故障,即当且仅当系统故障在被检测线路一端所引起的初始电压和电流暂态故障分量具有反极性关系时判断为正方向故障[6]。因此,在系统发生故障时,如果从被检测线路的任一端看,该故障均表现为正方向故障,则该故障必然是本线路内部故障,否则是外部故障。
2 接触网的暂态过程
2.1 接触网行波特点
牵引网中的短路故障主要是接触网和钢轨之间的短路故障,这也是最常发生的。在本文所搭建的AT接触网短路模型中将接触网和钢轨分别作为两相来处理,所以说接触网和钢轨之间的短路可以看作为是两相短路,求解故障量时按照两相短路来计算。由于两相短路不存在零序电流的通路,所以故障电流很大。而接触网供电的特点和电力输电线路的双端供电类似,因此可以看做是双端供电的电力输电线路[7]。当发生短路故障时,产生的故障暂态行波将以故障点位中心向两端传播。
而实际上由于分区所中保护装置的动作时间小于行波到达测量点的时间,故初始行波波头信号将先后到达测量点。可见,这种情况下行波的传播方式与电力系统双端供电的方式是一样的,如图2。

图2 接触网故障行波示意图Fig.2 Schematic diagram of catenary fault traveling wave
2.2 暂态信号的提取
无论是直流供电、AT供电、BT供电还是其它供电方式,牵引变电所都是向复线上下行接触网并联馈电,并且上下行供电臂的末端并联。当发生短路故障时断路器断开,之后很短的时间内重合闸再次闭合。如果只是瞬时性故障重合闸重合成功。如果是永久性故障重合闸则会再次断开,这也是本文研究的主要状态。当然重合闸的过程也会产生暂态行波这将对行波故障测距产生一定的影响。由于此过程相对较复杂本文暂时没有考虑这种情况,待以后研究。和普通输电线路暂态过程不同的是牵引供电系统中除了合闸、雷击外机车的停启等因素也会产生有许多的高次谐波及干扰信号,相比而言牵引供电系统的暂态过程更为复杂这也对行波保护在接触网中的应用制造了障碍[8]。行波信号的频率在10~100 kHz之间,如何在大量的暂态信号中排除干扰获得有效的行波信号成为了接触网行波保护重中之重,而小波变换法很好的解决了这个问题。
小波变换法是根据行波信号在其小流变换下的模极大值实现故障测距一种算法[9]。它的理论依据是由故障点产生的或线路开关合闸产生的初始行波、故障点的反射波、对端母线的反射波、噪声信号等在不同尺度下的小波变换都将呈现模极大值,根据不同尺度下的小波变换模极大值及其变化,并与接于同一母线的健全线路行波波形相比较,可以有效地识别出来自故障点初始行波和反射波,以实现故障测距。小波变换法被认为是有效的方法之一。
3 仿真及分析
在ATPDraw建立模型时忽略了线路之间的电磁耦合,整个牵引网分别按三相架空线的JMarti模型建立,接触网和承力索作为一相两分裂导线,钢轨作为一相两分裂导线,回流线作为一相导线。供电臂长为30 km,每隔10 km设置一个AT所。
3.1 无站场时的仿真结果分析
检测点分别安装在供电臂的两端母线m、n处,当距离牵引变电所6 km处发生短路故障时,通过仿真得到的短路电流如图3所示。由图3可以看出初始行波波头的到达时刻点分别652点和726点,本文所取的行波波速为光速,采用D型双端测距法计算得到故障点离牵引变电所的距离为6.018 km。
如果采用A型单端测距法(如图4所示),就需要检测有故障点反射回来的行波波头,由仿真得到初始波头和故障点第一次反射波头到达时刻点是66点和71点,经计算得故障距离为5.929 km。
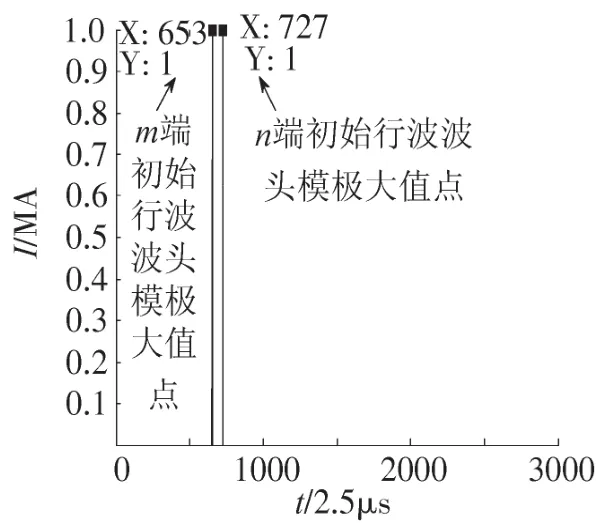
图3 6 km故障时D型测距法仿真波形Fig.3 6 km fault simulation waveform of the D-type ranging method

图4 6 km故障时A型测距法仿真波形Fig.4 6 km fault simulation waveform of theA-type ranging method
经过大量的仿真实验得到在无站场的情况下A型和D型测距法测距结果如表1所示。
3.2 有站场时的仿真结果分析
当线路上存在分支站场时的故障电流波形及其小波分析,如图5所示。从图中可以看到由于分支站场的存在线路中的反射行波变得非常复杂,再加之当故障超过线路的中点时还要区分对端母线的反射波,因此从众多的反射波中提取第一次故障反射波难度很大。此时A型测距法就不适用,而D型测距法只需初始行波,各种反射行波对其没有影响。图5为存在站场时6 km出发生短路故障时的初始行波波头到达测量点的时刻点仍然是652点和726点,计算得到故障距离同样是6.018 km。经大量仿真实验数据分析,在存在站场的情况下对D型行波测距的结果基本没有影响[10],测距结果如表2所示。

表1 A型和D型测距仿真数据Tab.1 Simulation data ofA-type and D-type ranging km

表2 D型测距仿真数据Tab.2 Simulation data of D-type ranging km

图5 存在分支站场时的故障仿真波形Fig5 Fault simulation waveform of branch station
4 结论
通过以上的仿真实验我们可以得出,D型测距法更适用于牵引网的行波保护,从仿真数据也可以看出其故障测距的结果更为精确,最主要的特点是其不受分支站场以及频繁的锚段电联结引起的反射行波的影响,完全可以单独使用。A型行波测距法受分支站场以及频繁的锚段电联结的影响很大,甚至无法检测出有效的反射行波,如图5所示,模极大值图中的反射行波的幅值大小相差不大,无法区分出故障点、母线以及分支点的反射行波。不受过度电阻的影响是行波保护的重要特点,并且故障电压相角对行波测距的结果影响也不大。当然故障电压过零点时由于故障电流很小会对行波测距产生一定的影响不过此种情况的发生概率很小,还待以后研究。
[1]曹笃峰.电气化铁道接触网行波故障测距研究[D].北京:北京交通大学,2007:12.
[2]毛志芳,和敬涵,周文.电气化铁道牵引网故障测距中行波法的应用[J].电气时代,2006(1):71-74.
[3]葛耀中.新型继电保护和故障测距的原理与技术[M].西安:西安交通大学出版社,2007:7.
[4]李伟,王倩,刘超.行波法应用于复线牵引网故障测距的仿真研究[J].铁道运输与经济,2008,6(6):89-95.
[5]杨毅波.超高压输电线路单端暂态量保护元件的研究[D].南昌:华东交通大学,2010:30-32.
[6]CHAOMING XIA,YIZHUANG HUANG.Study of algorithm based on the transient voltage signal transmission line protection[J].Electric Relay,2003(5):5-13.
[7] ZHINONG WEI,YUPING ZHENG,Hua He.Subway remote short-circuit current analysis based on wavelet transform[J].Power System Technology,2003,15(6):5-8.
[8]谢民.220 kV电网行波测距系统组网运行实践探讨[J].电力自动化设备,2010,30(5):136-138,41.
[9]徐伟宗,唐昆明.基于导数法的故障行波波头识别改进法[J].电网技术,2010,34(1):198-202.
[10]郑州,吕艳萍,王杰,等.基于小波变换的双端行波测距新方法[J].电网技术,2010,34(1):203-207.

