同信道干扰下相关多输入多输出信道容量分析
闫秋娜 岳殿武,2 王 谦
(1.大连海事大学信息科学技术学院,辽宁 大连116026;2.东南大学移动通信国家重点实验室,江苏 南京210096)
引 言
近年来,在发送端和接收端使用多个天线的多输入多输出(MIMO)无线通信系统由于极大地增加了信道容量,引起了广泛的关注。关于无线MIMO系统,人们已在多个方面对其进行了深入的研究,尤其是在信道容量方面。然而,迄今为止对信道容量的分析还主要集中在没有同信道干扰情况下的MIMO 系统[1]。
在蜂窝移动通信系统中,多个用户由于共享同一个射频频谱因此不可避免的引入了同信道干扰,从而严重地影响了系统提供给用户的服务质量。为此,不少学者开始对衰落环境下带有同信道干扰的MIMO信道容量进行研究[2-5]。特别是,Kang等人推出了MIMO信道容量矩生成函数(MGF)、均值和方差的精确闭式表达式[3]。然而,他们所考虑的仅是在Rayleigh衰落环境下通信用户的发送和接收天线阵都不相关的情况。在许多实际无线环境中,由于缺少散射条件,天线之间容易存在信号相关;此外,由于物理尺寸的限制,在移动终端使天线之间间隔较远是非常困难的,因此,也会使天线之间存在着空间相关性。最近,Wang等人研究了通信用户接收天线阵带有空间相关性的情景,并在存在同信道干扰情况下获得了MIMO Rayleigh衰落信道容量的分析结果[5]。
鉴于上述因素,本文侧重研究带有同信道干扰和发送相关的MIMO信道容量问题。主要针对通信用户和同信道干扰用户都处于Rayleigh衰落环境的情况。
复矩阵变量分布理论是本文所采用的主要分析工具。这个理论已经成功的用于不带有干扰的MIMO信道容量分析中[1]。
1.矩阵变量的超几何函数
1.1 矩阵变量超几何函数的定义
许多矩阵变量分布,特别是中心二次型分布,都能表示成矩阵变量的超几何函数形式[7-8]。矩阵变量的超几何函数是单变量超几何函数的一般化,而单变量的超几何函数已经被广泛地应用在科学与工程领域。下面给出复数域上矩阵变量超几何函数的定义,并讨论复矩阵变量超级几何函数与单变量超级几何函数之间的关系。
对于一个预先给定的正整数k,可用一个正整数向量k=(k1,k2,…,kp)表示k的一个划分。对于一个划分就意味着这些正整数分量之和为k.复多元的超几何系数可表示为

式中:(x)n=x(x+1)…(x+n-1)是Pochhammer符号[7]。
定义1[7]令X是一个p×p的Hermitian矩阵。则复矩阵变量超几何函数定义为

式中:a1,…,am;b1,…,bn是任意复数;表示对所有划分k的求和;Ck(F)是关于k的F的带状(Zonal)多项式。
为了证明第3部分中提出的定理1,需要给出两个矩阵变量的超几何函数的定义,下述定义虽然和James在文献[7]中所给出的定义在形式有些不同,但在本质上是一样的,就像在文献[1,8]中所使用的那样。
定义2[7-8]令p≤q,涉及两个 Hermitian矩阵X(p×p)和Y(q×q)的超几何函数定义为

式中各种符号所表示的含义同定义1,其详细讨论可参考文献[1,9]。
1.2 基于单变量超几何函数的表达式
矩阵变量的超级几何函数虽然便于理论上的分析,但不方便进行实际的数值计算。为此,讨论其与便于数值计算的单变量超级几何函数之间的关系。
一般Hermitian矩阵变量超几何函数可以由单变量超几何函数来表示。
一个p×p的对角矩阵Λ =diag(λ1,λ2,…,λp),(λ1>λ2>…>λp)的Vandermonde矩阵可表示为

引理1[1]令B是一个p×p的Hermitian矩阵。定义 Θ=eig(B)=diag(ω1,…,ωp),ω1> …>ωp,则关于矩阵B的超几何函数可表示为

式中:F=[fij],i,j=1,2,…,p,且该矩阵中元素可表示为单变量超几何函数:

如下面的引理2所述,两个Hermitian矩阵变量的超几何函数也能够由单变量超几何函数来表示。
引理2[1]令

再定义

则

式中:L=[lij],i,j=1,2,…,p,且该矩阵中元素可表示为单变量超几何函数:

引理1和引理2将会为矩阵变量超几何函数的数值计算提供方便。
2.MIMO系统模型
考虑一个带有t个发射天线和r个接收天线的无线通信系统。假定该系统是一个仅限干扰的系统,其加性噪声因影响比较微弱,可以在分析中忽略。设有l个干扰用户,每个干扰用户具有ti(i=1,…,l)根干扰天线。接收端接收的r×1阶向量可表示为

式中:H是服从高斯分布的r×t阶归一化信道复矩阵,H ~(0,Σ ⊗Ψ),Σ ⊗Ψ 是随机矩阵H 的协方差矩阵(参见文献[9]的第7章);s是一个t×1阶的归一化发射信号向量,且相关性为E(ss†)=Rs;Es是系统的总发射功率。同样,对于第i个同信道干扰,Hi是r×ti阶归一化干扰信道矩阵,si是ti×1阶干扰用户发射信号向量,其平均功率为Ei,且可假定 Hi~CNr,t(0,Σi⊗ Ψi),si~(0,Ri).
对于式(13)中的随机矩阵H和Hi,现给出进一步说明。矩阵H和Hi的相关性分别由Σ⊗Ψ和Σi⊗Ψi表示。Σ和Σi分别表示在接收端输入信号和干扰信号的r×r阶相关矩阵。Ψ表示发射天线阵列的t×t阶相关矩阵,而Ψi是第i个干扰的ti×ti阶相关矩阵。这些矩阵与天线阵列的结构、信道的特性等因素密切相关。
为了简明起见,和文献[2-5]类似,对接收机,其上所有的干扰信号si(i=1,…,l)都假定是不可知的,且都为复高斯向量。因此,在Hi(i=1,…,l)为已知的条件下,干扰为复高斯的,其协方差矩阵为

式中:

为了便于分析处理,首先假定Σ1=Σ2=…=Σl=Σ.注意 .这个假定的约束条件比起文献[2-4]更为宽松些。因为在这些文献中除了约束所有干扰的相关接收矩阵都是相同的之外,还要满足Σ1=Σ2=…=Σl=I.为了得到简化的闭式表达式,现进一步假设[5-6]

此外,还要假设接收端完美地知道信道状态信息,而发送端不知道。那么当发射信号不相关,即Rs=It时,系统能够获得最大瞬时容量,这时Rs是最优的。为此,可假定Rs=It,同时也假定

在上述所有的假设下,下面推导随机矩阵ρH†(Hi)-1H的统计表达式。其中

3.带有干扰的MIMO信道容量
3.1 矩生成函数和遍历容量
对于MIMO信道的输入向量s和式(11)给出的输出向量y,其瞬时互信息I(s,y)的表达式为[2-5]
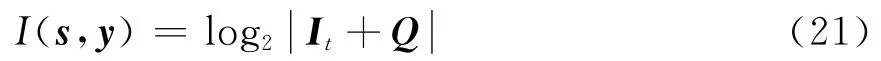
式中

令

CNr,tI(0,Ir⊗ItI)。则根据文献[9]中的定理7.4.1的证明,Q又可以表示为

于是MIMO信道的遍历容量可表示为

进一步互信息I(s,y)的矩生成函数可表示为

那么通过式(26)就可求得遍历容量[5]。

3.2 矩生成函数表达式
定理1 假设通信用户接收端天线数小于或等于所有干扰用户发射端天线数之和,即r≤tI,则互信息I(s,y)的矩生成函数可表示为


定理1之证明见附录A。
为了便于数学处理,在MIMO系统的性能分析中通常要采用r≤tI的假设[3,5-6]。这个假设特别符合移动通信下行传输情况,因为体积小、重量轻的手提或便携式发送终端实际上只能安装一两个天线。
3.3 MIMO信道的遍历容量
现给出基于单变量超几何函数的MIMO系统遍历容量表达式。
定理2 假设r≤t1,并令Λ =eig(It-)=diag(λ1,λ2,…,λt),λ1<λ2< … <λt。则 MIMO遍历容量可表示为

式中

定理2之证明见附录B.
4.数值结果
下面要用数值结果验证分析结论的正确性,讨论各种系统参数对MIMO系统遍历容量的影响,并与已有的文献结果[4-5]进行比较。
为了简明起见,只利用文献[12]中的指数模型来描述发送端和接收端天线之间的相关性:
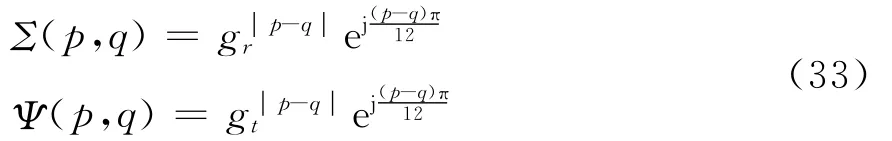
式中gr和gt分别表示接收端和发送端天线阵的相关系数,范围从0到1,增加表示天线之间的相关性增强。
将发送端天线之间和接收端天线之间的相关系数分别设置为0.1和0.5,然后固定发送端天线数目为2.在图1中,对不同的接收端天线数目和总干扰发送天线数目下的信道容量理论分析结果进行蒙特卡罗仿真验证。为了使统计结果可靠,蒙特卡罗仿真实验次数取定为106,以下同。从图1可以看出,理论数值结果和蒙特卡罗仿真结果非常匹配,从而验证了理论分析结果的正确性。
在图2中,对不同的发送端天线阵相关系数下的信道容量进行数值比较。为了公正的比较,其他参数的设置相同,即t=2,r=3,tI=4,gr=0.5.从图2可以发现,理论结果和仿真结果非常符合,且相关性越高,容量越小,这符合MIMO空间相关性对性能负面影响的特征。并且还可以看出,强的空间相关性对遍历容量的影响是非常大的,尤其是在高信干比的区域。

图2 不同发送端天线阵相关系数信道容量与ρ的关系曲线
在图3中,对不同的总干扰发射天线数目下的信道容量进行了比较。图中信干比(SIR)是接收信号和干扰信号功率之比,可表示为


图3 不同总干扰发射天线数目下信干比的信道容量
从图3可以看出,当干扰天线的数量增加时,容量会降低,但降低的幅度逐渐变小。这是因为在同样条件下干扰天线的数量多比数量少所形成的干扰统计方差会更高些,但随着数量增多,该方差也逐渐收敛到一个固定值。
在干扰天线数tI=4、发送天线数t=4和接收天线数r=4情况下,图4比较了发送空间相关性和接收空间相关性对遍历信道容量的影响。图4共画了四条曲线,其中两条曲线对应发送相关参数取gt=0.2,0.6两种情况,而其他两条对应接收相关参数取gr=0.2,0.6两种情况。从图4可见,尽管空间相关性参数选取一样,发送相关性和接收相关性都对遍历信道容量产生影响,但发送空间相关性随着相关参数增加对遍历信道容量影响越来越严重,且明显超过接收空间相关性的影响。

图4 发送相关性和接收相关性对遍历信道容量的影响比较
在干扰天线数tI=6和接收天线数r=3情况下,对于不同发送天线数目,图5侧重比较了有和没有发送空间相关性对遍历信道容量的影响。图5对比了t=2,4,6三种情况。从图5可见,随着发送天线数增加,不论有没有空间相关性,遍历容量均越来越大。空间相关性虽然会使遍历容量有所影响,但这影响并不随发送天线数变化而明显发生变化。

图5 不同发送天线数目下发送空间相关性对遍历信道容量的影响
在发送天线数t=3和接收天线数r=3情况下,图6比较了同信道干扰和发送空间相关性对遍历信道容量的影响。图6中虚线表示没有干扰也没有空间相关性情况,其他四条曲线中临近虚线的两条曲线对应相关参数取gt=0.6,0.9两种情况,另外两条对应干扰天线数取tI=6,9两种情况。从图6可见,尽管同信道干扰和发送空间相关性都对遍历信道容量产生影响,但空间相关性影响是有限的,而同信道干扰随着干扰天线数目增加越来越严重,明显超过空间相关性的影响。

图6 同信道干扰与发送空间相关性对遍历信道容量的影响比较
5.结 论
在Rayleigh衰落环境下,深入地研究了具有同信道干扰和发射空间相关性的MIMO信道容量问题。在假定当接收端完美地知道信道状态信息而发射方不知道情况下,利用矩阵变量分布理论,首先推导出MIMO信道互信息的矩生成函数的精确闭式表达式,然后通过该表达式可进一步得到MIMO遍历容量的精确表达式。可见,对MIMO衰落信道容量的分析在很大程度上要依赖于矩阵变量分布理论。
由于数学处理的难度,在系统模型中还不得不加入了一些限制和约束。因此,就一般模型而言,带有同信道干扰和空间相关性的MIMO信道容量问题依然是一个没有彻底解决的困难问题。这将需要更复杂、更有力的数学工具来帮助解决。
[1]KIESSLING M.Unifying analysis of ergodic MIMO capacity in correlated Rayleigh fading environments[J].European Transactions on Telecommunications,2005,16(1):17-35.
[2]KANG M,YANG L,ALOUINI M S.Performance analysis of MIMO channels in presence of co-channel interference and additive Gaussian noise[C]//Proc the 35th Annual Conference on Information Sciences and Systems.Baltimore,2003.
[3]KANG M,ALOUINI M S.Capacity of MIMO Rician channels with multiple correlated Rayleigh co-channel interferers[C]//Proc IEEE Global Telecommun Conf.San Francisco,2003:1119-1123.
[4]KANG M,YANG L,ALOUINI M S.Capacity of MIMO channel in the presence of co-channel interference[J].Wireless Communications and Mobile Computing,2007,7(1):113-125.
[5]WANG Y,YUE D W.Capacity of MIMO Rayleigh fading channels in the presence of interference and receive correlation[J].IEEE Transaction on Vehicular Technology,2009,58(8):4398-4405.
[6]KANG M,ALOUINI M S.Quadratic forms in complex Gaussian matrices and performance analysis of MIMO systems with co-channel interference[J].IEEE Transaction on Wireless Communications,2004,3(2):418-431.
[7]JAMES A T.Distributions of matrix variates and latent roots derived from normal samples[J].Ann Math Stat,1964,35(2):475-501.
[8]KHATRI C G.On the certain distribution problems based on positive definite quadratic functions in normal vectors[J].Ann Math Statist,1966,37(2):468-479.
[9]GUPTA A K,NAGAR D K.Matrix Variate Distributions[M].NewYork:Chapman& Hall/CRC,2000.
[10]KHATRI C G.Classical statistical analysis based on a certain multivariate complex Gaussian distribution[J].Ann Math Statist,1965,36(1):98-114.
[11]CHIANI M,WIN M Z,ZANELLA A.On the capacity of spatially correlated MIMO Rayleigh-fading channels[J].IEEE Trans Inform Theory,2003,49(10):2363-2371.
[12]ZHANG Q T,CUI X W.Outage probability for optimum combining of arbitrarily faded signals in the presence of correlated Rayleigh interferers[J].IEEE Transactions on Vehicular Technology,2004,53(4):1043-1051.
[13]YAN Q N,YUE D W.Matrix variate distributions and MIMO channel capacity[C]// Conference Proceedings of 2009International Institute of Applied Statistics Studies.Qingdao,China,2009:386-394.

