基于三角面元剖分的全波信号完整性建模方法
孔 繁 王 昊 盛卫星 武 景
(南京理工大学电子工程与光电技术学院,江苏 南京210094)
其中:fm是第m个部分元对应的测试函数,内积函数定义为
引 言
随着集成电路的快速发展、高速接口的普遍应用,高速印制板(PCB板)上的信号完整性(SI)问题越来越突出[1-3]。临近的PCB板走线之间、元件之间电磁耦合的影响变得不能被忽略。寄生电感和电容,信号延迟和不连续点的反射都会破坏信号质量。简单的电路理论分析信号完整性问题在GHz信号甚至更高频率信号面前显得力不从心。电磁场分析方法被越来越多地应用到SI分析中,如时域有限差分法(FDTD),有限元法(FEM),矩量法(MOM)等等,其中部分元等效电路(PEEC)方法因其能将电磁场问题转化为等效的电阻、电容、电感的电路问题而越来越受欢迎。最早出现的PEEC方法[4]可以对多导体的电磁互耦问题进行建模。通常使用四边形的PEEC单元对导体进行剖分。因此,对于复杂几何形状导体,要得到精细的剖分,并考虑到电磁场的传播特性,对电场积分方程的离散而产生的密集矩阵规模是相当巨大的。同时得到的电路模型的规模随着分析问题的复杂度增加也将是异常庞大的,因而就出现了对PEEC的模型简化。对PEEC的简化前人做了不少工作。采用快速多极子的方法[5-6],可以从格林函数计算的角度对PEEC方法的计算量进行缩减。通过模型降阶技术(MOR)[7-9]技术对PEEC得到的模型进行简化。一种新型基于物理概念的模型降阶技术(PMOR)[10],用于分析一个参数化过程中所产生的部分元等效电路矩阵,该技术保证了整体稳定性,是一种被动的降阶模型参数化方法。一种加入了磁体的磁化电流、导体的传导电流和介质的极化电流的扩展等效电路模型[11]也已经出现。经典的PEEC方法依赖于对目标结构进行纵向剖分。对于非标准矩形的结构要通过使用非标准矩形的共面四边形的PEEC剖分方法[12]来计算。分析对象形状不规则例如不平行走线就需要一种分析不平行走线的PEEC计算方法[13],而且使用的是准静的解析解结果计算分布参数。将矢量面电流RWG(Rao-Wilton-Glisson)基函数用于 PEEC 问题[14],使用自由空间格林函数,分析两根平行走线的自由空间情况下的S参数计算。但是,该方法使用简单的解析解只适合求解自由空间问题,而准静格林函数也只能在低频段适用,随着频率的升高,准静的格林函数将出现不准确的结果。使用DCIPEEC方法[15],将离散复镜像(DCIM)引入到PEEC模型的建立,仿真的微带结构的S参数,但该方法使用简单的矩形脉冲基,分析规则的矩形结构可以适用,如果遇到非直角走线等结构则不能进行有效的剖分。而且,以上文献都停留在S参数的仿真计算,没有从高速数字信号传输眼图的角度对信号完整性进行优化或验证。
针对任意形状PCB走线的信号完整性(SI)分析问题,采用RWG基函数和三角形PEEC单元对PCB走线进行有效剖分,推导了电路模型及其计算公式,并采用了DCIM来计算格林函数,提高了PEEC模型的精确度。还采用该 RWG-DCIMPEEC对微带螺旋电感和带不同形式拐角的高速PCB差分对线进行了仿真计算,根据所提取的电路模型参数、芯片制造商提供的集成电路的SPICE模型或者IBIS模型,利用HSPICE工具软件仿真了高速数字信号传输时的眼图,并从眼图和传输误码率的角度对高速PCB差分对线的拐角参数进行了优化设计。最后给出了实际测量的PCB板走线和S参数采用RWG-DCIM-PEEC的计算结果,验证了RWG-DCIM-PEEC方法的正确性。
1.理论分析
RWG基函数最先是由Rao,Wilton和Glisson提出来的[16]。三角形剖分方法在对复杂形状导体进行剖分时的表现要比矩形更好。RWG基函数是一种定义在剖分后第n条公共边上的矢量基函数,其定义如下:


其散度为:式中:ln是第n条公共边的边长;是三角形的面积;和分别是三角形面、自由顶点所对应的矢量,称为自由矢量。第n条边上参考电流的正方向定义为从流向.r代表坐标系原点到计算源点或场点的位置向量。图1示意了经剖分后与第n条公共边相对应的两个三角形对和及其参数。
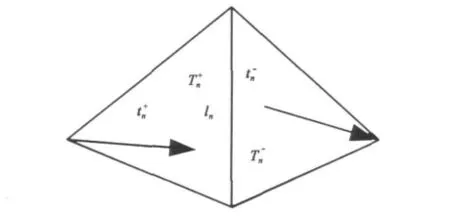
图1 经三角形剖分后与第n条公共边相对应的两个三角形对及其参数的示意图
离散后第n条公共边称为PEEC的一个单元(也叫部分元)。设经过剖分后,共有N个部分元。则被剖分的导体面上的面电流密度可以近似地表示为各个部分元电流密度与其矢量基函数乘积的和,即

其中,电流系数Jn表示流过第n条公共边的电流密度。在没有外加激励时,环路的电压为零,即满足

式中:A为矢量磁位;Φ为标量电位;σ为电导率。公式(4)中第1至第3项分别代表等效电阻、电感和电容引起的电压降。对公式(4)的各项以部分元为单位分别用RWG基函数形式的测试函数在频域做内积处理,得到
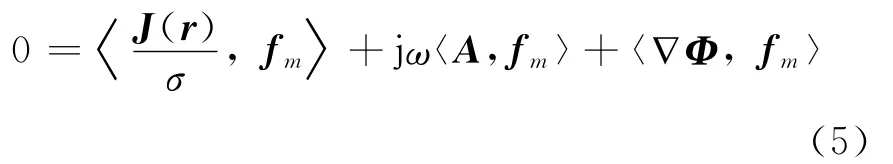
其中:fm是第m个部分元对应的测试函数,内积函数定义为

式中,积分区域S为与第m个部分元相对应的两个三角形对所在的区域。具体到两个剖分单元的等效电路形式如图2所示。

图2 两个RWG剖分单元的等效电路
单元S1包含两个三角面元A1和A2,A1和A2的公共边l1作为离散的电流支路I1;单元S2包含两个三角面元A2和A3,相应的公共边l2对应于电流支路I2.三个面元A1、A2、A3对应于三个节点电位Ф1、Ф2、Ф3.
经推导,公式(5)第2项中当用f1作为测试函数时电感的表达式可以写为

式中:l1和l2是公共边的边长;G(r,r′)是格林函数,ω是角频率;电感L1,1定义为自感;L1,n为互感。公式(7)中互感带来的电压降可以用电流控制电压源(CCVS)的形式来表示。
公式(5)第3项以f1做为测试函数,可以推导出节点电位方程。公式(8)中的pmn(m=1,2;n=1,2,3)是电位系数。p11是自电位系数,p12、p13是互电位系数,互电位系数带来的电压降可以等效成电流控制电压源(CCVS的形式,其控制电流是节点到地之间定义的电流由支路电流I1,2决定。J1和J2是定义在相应的公共边上的电流密度。-Φ1+Φ2表示两个节点之间的电压降。

公式(5)的第1项为PEEC单元等效电阻(又叫部分电阻)产生的压降。部分电阻的定义如下
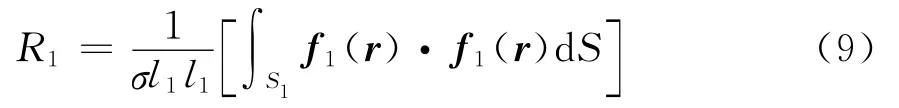
在计算无限薄导体时可以当作是理想导体处理,即电阻项可以忽略不计。在实际的计算中均假设为理想导体情况忽略电阻项的计算,因此,在图2中我们也省略了电阻项。
上式中的格林函数采用DCIM方法[17]求取,如图3所示的微带结构。
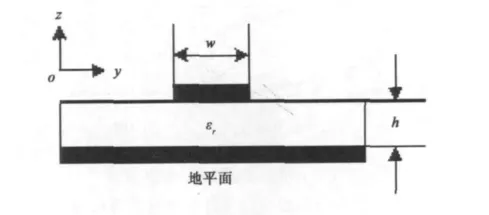
图3 微带结构示意图
如图3所示微带结构位于xoy平面,介质介电常数是εr,厚度为h,微带上的感应电流可以通过上述方法求解混合位积分方程得到,其中的标量位和矢量位可以分别表示成

GA包含四个分量,然后在图示平面结构中,未知电流值有xx和yy分量,这两个分量可以用Ga和Gq分别表示格林函数中的磁场矢量位和电场标量位。因此,空域格林函数可以从相应的谱域格林函数通过汉克尔变换得到

离散复镜像方法先从谱域格林函数中抽取准动和表面波项,再将剩余的部分通过矩阵束方法拟合成指数闭式表达形式。式中的Ga和Gq可以表示成下面的形式。第1部分是准动镜像部分,主要是在进场起作用,如下式所示。

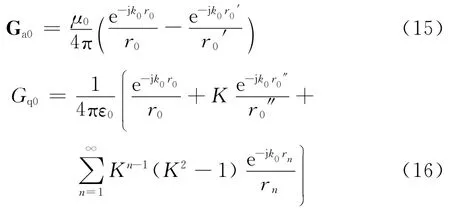
第2部分是漏波的表达式,在中场区起作用。

第3部分是表面波部分,主要是在远场区起作用。
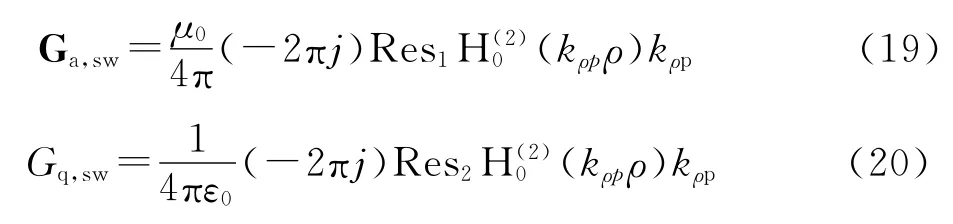
2.实验结果分析
通过4个例子来验证RWG-DCIM-PEEC方法的正确性,并对其性能进行评估。例子1是一个微带螺旋电感器模型(见图4(a)左侧)。其线宽和线间距均为1mm,介质板厚度为0.15mm,介电常数为4.3.图4(a)的右侧部分是该螺旋电感器经三角形剖分后的结果。图4(b)显示了分别采用RWGDCIM-PEEC方法、基于矩量法(MoM)的IE3D软件和准静的PEEC方法计算得到的该螺旋电感S参数幅度和相位。
从图4(b)的结果可以看到:RWG-DCIM-PEEC方法和IE3D计算的结果能够很好地吻合。表明RWG-DCIM-PEEC本质上是与矩量法相近的精确的全波分析方法。而准静的PEEC方法的计算结果则与RWG-DCIM-PEEC方法和IE3D的有误差。
例子2是一个PCB板上的不平行走线模型(见图5(a))。两根微带走线线宽均为1mm,夹角为30°,介质板厚度为0.15mm,介电常数为4.3.图5(b)显示了分别采用RWG-DCIM-PEEC方法和基于矩量法(MoM)的IE3D软件计算得到的这两根不平行走线的S参数幅度和相位。
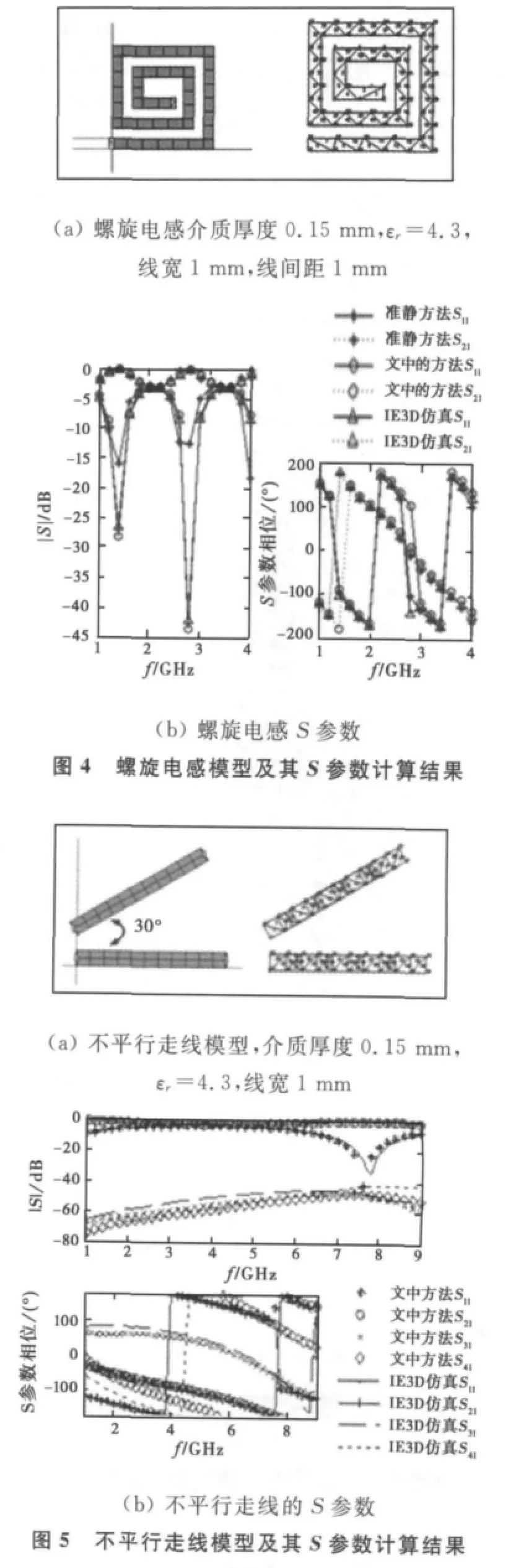
不平行走线模型对于矩形剖分的传统PEEC方法需要做特殊处理,也就是要区别处理不平行单元与平行结构单元,相当于增加了程序的复杂度。而使用RWG基的RWG-DCIM-PEEC方法不需要特别处理不平行单元,由于RWG基的矢量基特性,程序中不用专门区分不平行结构,简化了算法。图5(b)中IE3D计算结果和 RWG-DCIM-PEEC方法计算结果一致,这也验证了RWG-DCIM-PEEC方法对不平线结构的分析计算的有效性。

例子3是带拐角的PCB走线。拐角是PCB走线中常遇到的结构,通常情况下采用45度拐角,图6(a)中给出了4种不同形式的45度拐角PCB走线模型。线形1中拐角处的线宽窄于走线线宽,线形2为近似圆弧拐角的形式,线形3中拐角处线宽与走线线宽相同,线形4中拐角处线宽不等于走线线宽但采取切角连接的形式。用RWG-DCIM-PEEC方法计算这四种不同线形的电路模型,得到节点单元电压和支路电流参数,根据这些参数可以很方便地得到输入阻抗等电路参数。利用RWG-DCIMPEEC方法对4种不同形式的45°拐角PCB走线进行分析和优化设计,使得其S21参数尽可能接近端接阻抗相应的S21参数(设定端接阻抗为50Ω)。考虑现阶段在PCB上的互连高速信号线所传输的是数字信号速率在2~3.125Gbps,所以在2~3GHz的频带内传输线的传输特性最优是我们追求的目标。利用RWG-DCIM-PEEC方法计算得到的阻抗见图6(b)。由图6(b)中可以看出:在设计频段内经过参数优化的线形1的阻抗始终高于其他类型走线,由此设计出的走线传输特性也好于其他类型。图6(c)是使用RWG-DCIM-PEEC方法计算得到的S21参数,与上面的阻抗相对应,线形1的S21参数在设计频段内好于其他形式。

眼图仿真采用速率为2Gbps的二进制数字信号,由图7的仿真结果中可以看出:最差情况线形4眼图涨开幅度由1v下降到600mv,经过优化的线形1在眼图的中间采样时刻有800mv,而且眼图边沿更清晰,说明信道质量优于其他情况。
最后给出的是PCB走线实验板的实测S参数数据与仿真数据的对比。实际的PCB走线如图8中(a)所示,采用微带走线形式。测量仪器采用安捷伦公司的86100C宽带示波器,测量结果可以使用标准的S参数.s2p文件导出,方便与仿真结果对比。

从对比结果中可以看出:仿真结果的S11和S21参数与实际测试的结果吻合非常好,验证了方法的正确性。
3.结 论
理论分析表明RWG-DCIM-PEEC方法是一种有效的建立SI模型的方法。RWG基应用于PEEC方法可以使得电流走向的定义更精确。实验和仿真结果验证了DCIM应用于PEEC之后与准静方法比较提高了高频条件下的准确性。RWG-DCIMPEEC方法得到的模型与HSPICE可以很好地兼容使用。但是,使用了DCIM的全波模型后,计算量也有所增加,今后我们会在这方面做更多的研究。
[1]刘学观,江盼盼,郭辉萍,等.高速数字信号在PCB中的传输特性分析[J].电波科学学报,2009,24(3):498-517.LIU Xueguan,JIANG Panpan,GUO Huiping,et al.Transmission characteristics of high-speed digital signal in PCB[J].Chinese Journal of Radio Science,2009,24(3):498-517.(in Chinese)
[2]袁智勇,何金良,陈水明.印刷电路板差分线边缘布置的电磁兼容分析[J].电波科学学报,2004,19(6):691-693.YUAN Zhiyong, HE Jinliang,CHEN Shuiming.EMC analysis for the edge placement of differential lines on the printed circuit board[J].Chinese Journal of Radio Science,2004,19(6):691-693.(in Chinese)
[3]陈建华,牛中奇.保护带对不同参数微带线信号和噪声的影响[J].电波科学学报,2010,25(1):53-58.CHEN Jianhua,NIU Zhongqi.Effect of guard trace on signal integrity and coupling noise of microstrips with different parameters[J].Chinese Journal of Radio Science,2010,25(1):53-58.(in Chinese)
[4]RUEHLI A E.Equivalent circuit models for three dimensional multi conductor systems[J].IEEE Trans Microwave Theory Tech,1974,22(3):216-221.
[5]ANTONINI G.Fast multipole method for time domain PEEC analysis[J].IEEE Trans Mobile Compute,2003,2(4):275-287.
[6]ANTONINI G,RUEHLI A E.Fast multipole and multifunction PEEC methods[J].IEEE Trans Mobile Compute,2003,2(4):288-298.
[7]SLONE R D,SMITH W T,BAI Z.Using partial element equivalent circuit full wave analysis and Pade via Lanczos to numerically simulate EMC problems[C]//International Symposium on Electromagnetic Compatibility,August 1997:608-613.
[8]KNOCKAERT L,DE ZUTTER D.Laguerre-SVD reduced order modeling[J].IEEE Trans Microw Theory Tech,2000,48(9):1469-1475.
[9]ODABASIOGLU A,CELIK M,PILEGGI L T.PRIMA:Passive reducedorder interconnect macromodeling algorithm[J].IEEE Trans Comput-aided Design Integr Circuits Syst,1998,17(8):645-654.
[10]FERRANTI F,ANTONINI G,DHAENE T,et al.Physics-based passivity-preserving parameterized model order reduction for PEEC circuit analysis[J].IEEE Trans on Copmponents Packaging and Manufacturing Technology,2011,1(3):399-409.
[11]ZHANG Xiao,CHEN Wenhua,FENG Zhenghe.Novel SPICE compatible partial-element equivalent-circuit model for 3-D structures[J].IEEE Trans Microw Theory Tech,2009,57(11):2808-2815.
[12]ANTONINI G,ORLANDI A,RUEHLI A E.Analytical integration of quasi-static potential integrals on nonorthogonal coplanar quadrilaterals for the PEEC method[J].IEEE Transactions on Electromagnetic Compatibility,2002,44(2):399-403.
[13]CRACRAFT M A,DREWNIAK J L.Analysis of distributed coupling along nonparallel traces using PEEC with phase term expansions[C]//IEEE International Symposium on Electromagnetic Compatibility,2008:1-6.
[14]WANG Y,JANDHYALA V,SHI C J R.Coupled electromagnetic-circuit simulation of arbitrarilyshaped conducting structures[C]//Electrical Performance of Electronic Packaging.Cambridge,2001:233-236.
[15]ZONG Z Y,WU W,FANG D G.Ultra-wideband EM modeling using DCI-PEEC method[C]//Proceedings of 2010IEEE International Conference on Ultra-Wideband,2010:1-4.
[16]RAO S M,WILTON D R.Electromagnetic scattering by surfaces of arbitrary shape[J].IEEE Transctions on Antennas and Propagation,1982,30(3):409-418.
[17]YANG J J,CHOW Y L,FANG D G.Discrete complex images of a three-dimensional dipole above and within a lossy ground[J].IEE Proceedings H:Microwaves,Antennas and Propagation,1991,138(4):319-326.

