基于改进型蚁群算法的阵列天线综合

赵小莹 柯腾龙 丁忆涵

（北京航空航天大学电子信息工程学院，北京100191）

引 言

采用阵列天线可以提高天线增益和辐射效率，控制波束、降低副瓣电平，或是对某个特定方向产生零陷抑制，使系统达到更好的电磁兼容性［1－2］。因此，阵列天线方向图的综合技术和相关优化算法越来越受到重视。阵列天线方向图综合一般是通过改变阵元激励的幅度、相位或位置等多个参量使天线阵的远区方向图满足所需要求。

阵列天线综合的传统方法有Chebyshev综合法和Taylor综合法［2］，但是由于天线优化过程中的目标函数或约束条件呈多参数和非线性的特点，传统的阵列天线综合方法无法有效地求得工程上的满意结果。随着计算机技术的发展，近几年来应用仿生优化算法对阵列天线进行综合已成为研究的热门课题［15］。 遗传算法 （GA）［8－10，13］和粒子群算法（PSO）［12，14］已被广泛地应用到优化阵列天线的方向图综合领域。作为另一种智能仿生算法，本文采用蚁群算法［3］（ACO），以天线阵元的激励为待优化变量，以阵列天线副瓣电平和给定方向产生零陷抑制为设计目标，对阵列天线的方向图进行优化。

蚁群算法是一种基于蚁群在觅食过程中寻找食物与蚁巢间最短路径的原理而发展起来的一种智能仿生算法。蚁群算法由Marco Dorigo于1992年在他的博士论文中提出，一直受到广大学者的研究和关注。蚁群算法收敛速度快，鲁棒性强，在解决旅行商问题［4］（TSP）、车业作业调度问题［5－6］（JSP）等问题中都取得了不错的效果。在优化天线阵列领域，文献［7］中，将天线阵阵元的激励置成1或0（即只有‘开’和‘关’两种状态），利用蚁群算法，优化了稀布阵问题。由于传统蚁群算法对离散问题非常有效但难以优化连续函数问题，所以目前将蚁群算法应用到阵列天线综合领域还极少见文献报道，而连续函数优化是现代阵列天线综合技术必需解决的问题。其他智能仿生算法大部分本就适用于连续函数优化，例如文献［13］［14］通过优化可连续改变阵元的激励幅度，达到降低副瓣电平并且对某些特定方向产生零陷抑制的天线阵方向图设计的目的。

为了解决传统蚁群算法对于构建蚂蚁路径时的离散性和阵列天线函数的连续变量之间的矛盾，本文提出一种改进型的蚁群算法，该算法将函数的连续变量进行不整编码，并根据连续变量的特点，在变量邻域内同样更新信息素。针对于传统蚁群算法易于收敛到局部最优解的缺点，引入最优点邻域搜索［11］，在提高算法的收敛速度的同时，也在一定程度上提高了算法的最优解搜索能力。

本文首先对基本蚁群算法进行简介，然后详细阐述了改进型蚁群算法的技术要点，最后通过引入4个实例表明采用改进型蚁群算法进行阵列天线综合是可行且有效的。并在实例中与相关文献的遗传算法［13］和粒子群算法［14］进行比较，仿真结果表明本文方法具有一定的优势。

1.基本蚁群算法介绍

基本的蚁群算法可以用蚁群算法解决TSP问题的例子来予以说明［4］。TSP问题是指：在给定的n个城市，找出一条最短的经过所有城市并且每个城市都只经过一次的封闭路线。假设有m只蚂蚁，城市i和城市j之间的距离为dij（i，j＝1，2…，n），在t时刻，城市i和城市j之间的信息素大小为τij（t），蚂蚁根据信息素的大小，来确定下一步选择的城市。在t时刻蚂蚁k由原来的城市i向城市j移动的概率表示为（t），概率的计算公式为

式中：ηij为启发因子；这里ηij＝1/ddij；Tabuk表示蚂蚁k已经走过的城市；α和β表示用于调节信息素强度和启发式信息强度的系数。当每只蚂蚁都完成一次遍历之后，需要对信息素进行更新。信息素的更新公式为

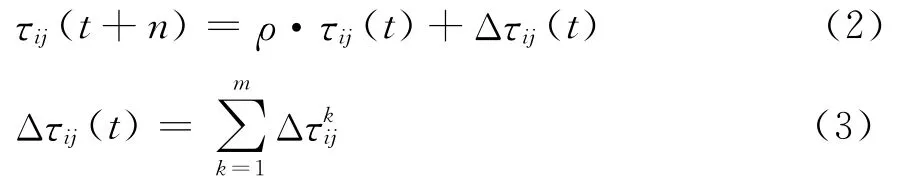
式中，ρ为信息素残留因子，范围为0到1之间。

基本蚁群算法优化的变量都是离散的，而阵列天线方向图综合问题的待优化变量如天线阵元的激励，均是连续性的变量，所以基本蚁群算法并不适用于阵列天线方向图综合问题。

2.改进型蚁群算法

2.1 目标函数分析

本天线阵方向图综合的问题，考虑为一个由2n个各向同性天线阵元组成的等间距直线阵列天线，其阵元的激励电流幅度为对称的，通过调整每个阵元的激励电流的幅度使得天线阵列的方向图达到预期的特性指标。天线阵的阵因子可以表示为

式中：Is为在天线阵列中的第s个阵元的激励幅度；d为阵元间的距离；α＝kdcosφ0，当且仅当φ＝φ0时F（φ）最大，即主瓣指向的方向为φ0方向。

对于本天线阵方向图综合，考虑的方向图的特性指标为最大副瓣电平和指定位置上的零陷深度，所以将优化的目标函数定义为

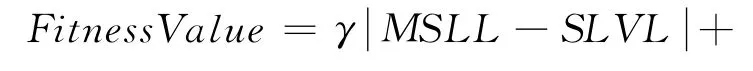
式中：SLVL为最大旁瓣电平的期望值；MSLL为计算得到的实际方向图的最大旁瓣电平；NLVL为零陷深度的期望值，并且期望在φi角度上获得零陷，其中当MSLL＜SLVL时令γ｜MSLL－SLVL｜项为0，当（φi）＜NLVL时令项为0.

2.2 不整编码寻优

针对阵列天线综合这个多变量连续函数优化问题，将每个天线阵元的激励幅度In都限定在0到1之间，在精度允许的情况下，将每个激励变量都分成m等分，于是构成了m×n个离散点，从而将n个变量的连续函数优化问题转换为在m×n个离散点选择出n个点的离散优化问题。

每个蚂蚁都从把第一个阵元作为起点，将最后一个阵元作为终点，当蚂蚁从第一个阵元走到最后一个阵元的时候，每个蚂蚁构成一个解。这里将信息素定义在每个离散的点上，而不是定义在路径上。第k只蚂蚁，在第i个阵元上，在m个点中选择第j个点的概率为

式中：α用于调节信息素强度；τij表示为在第i个阵元的第j个等分点上的信息素，如果在第i个阵元上选择了第j个等分点，就代表蚂蚁k在第i个阵元上选择的激励为j/m.当每个蚂蚁都完成各自遍历之后，将每个蚂蚁的路径都转换为相应的激励，并计算天线阵的远场方向图，最后计算目标函数的值。

2.3 邻域优化

尽管将天线阵列方向图综合问题进行了离散化处理，但其本质上仍是连续性问题。在这里，根据该问题连续性的特点，通过引入了最优解邻域寻优和邻域信息素更新，来进一步提高算法的寻优能力。

在所有的蚂蚁都完成一次遍历后，进行最优解的邻域寻优［11］。最优解的邻域寻优主要是在该次迭代最优解的路径上的一个邻域范围内，随机选出若干条新的路径，并计算这些新路径的目标函数值，如果在这些新路径中寻找到了比原来的最优路径更好的路径，则用该新路径替换掉原来的最优路径。最优解的邻域寻优可以加快算法的收敛速度和寻优能力，但是在邻域范围内搜索过多的路径也会大大增加算法的复杂度。在这里，假设一共有ant只蚂蚁，则邻域内的搜索路径条数应该控制在ant/4以内。

蚂蚁完成遍历并且完成邻域寻优后，最后进行信息素的更新。信息素的更新分两个步骤进行。首先进行的是信息素的全局更新。假设共有ant只蚂蚁，在第t次迭代中，信息素的全局更新按照如下规则进行

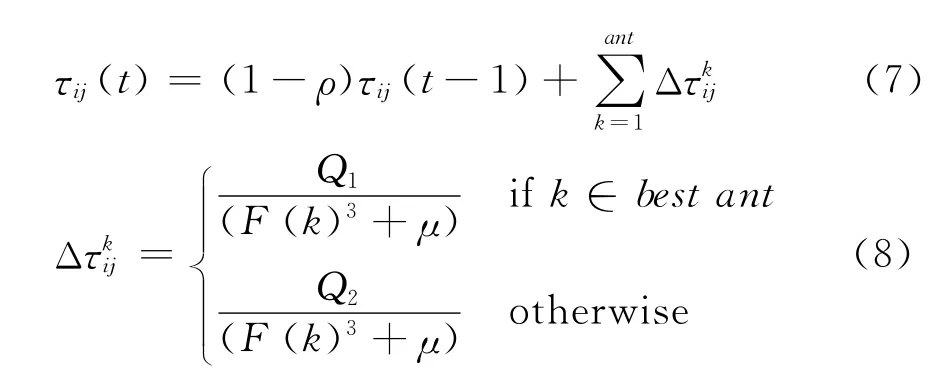
式中：F（k）代表的是第k只蚂蚁的目标函数值；ρ为信息素蒸发系数。在这里μ可以取10～15之间，另外Q1和Q2为信息素增强系数，一般取Q1＝3Q2，从而在最优的路径上增加更多的信息素，大大提高算法的收敛速度。在完成信息素的全局更新之后，进行信息素的邻域更新，即在每个蚂蚁的遍历路径上经过点的附近，也同样增加一定的信息素，用来表示第k只蚂蚁邻域上的信息素增加量

式中χ一般可以取2到5之间。

3.应用举例

优化对象选取为线性对称天线阵列，阵元为理想点源，忽略了阵元互耦、阵元通道幅相误差等因素的影响。算法中权系数γ和δ分别取1和0.15，蚂蚁数ant取为60，不整编码等分数m＝600，调节信息素强度系数α取为1，信息素增强系数Q1取为1.5.

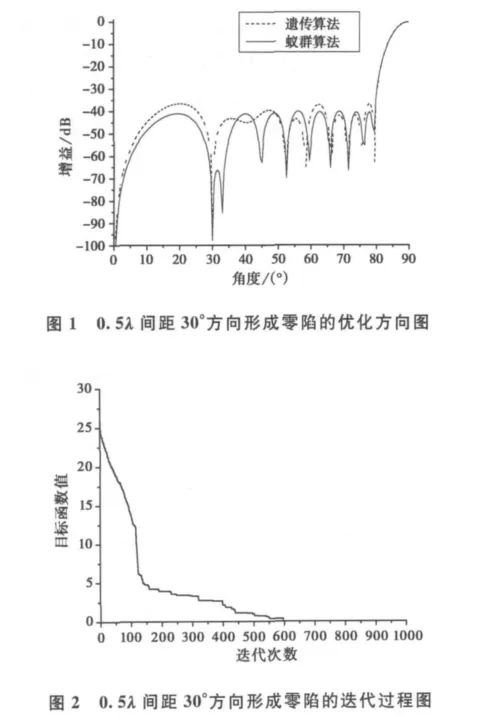
［例1］设计指标：n＝10，即天线的阵元个数为20个，阵元间距d＝0.5λ，主瓣对准90°方向，SLVL＝－40dB，NLVL＝－90dB，30°方向形成零陷。

在经过1 000次迭代后，优化结果如下：其阵元的 电 流 激 励 幅 度 依 次 为 0.94，0.908 33，0.82，0.731 67，0.595，0.48，0.348 33，0.236 67，0.158 33，0.093 33，其方向图如图1所示，最大副瓣电平为－40.077dB，零陷深度为－97.776dB，满足了设计指标，比基于双种群遗传算法的文献［13］的最大副瓣电平和零陷深度分别降低了3.421 1dB和6.496 6dB.其迭代过程图如图2所示，在大约150次迭代时，目标函数f就已经收敛到5附近，收敛速度较快。

［例2］设计指标：n＝10，即天线的阵元个数为20个，阵元间距d＝0.4λ，主瓣对准90°方向，SLVL＝－40dB，NLVL＝－90dB，30°方向形成零陷。

在这里不整编码等分数m＝1 000，其他参数保持不变。在经过1 000次迭代后，在经过1 000次迭代后，优化结果如下：其阵元的电流激励幅度依次为0.964，0.96，0.811，0.812，0.551，0.572，0.296，0.312，0.114，0.134，其方向图如图3所示，最大副瓣电平为－41.36dB，零陷深度为－95.672dB，比文献［13］中的最大副瓣电平和零陷深度分别降低了5.821 8dB和3.737 7dB，方向图如图3所示。

［例3］设计指标：n＝10，即天线的阵元个数为20个，阵元间距d＝0.5λ，主瓣对准90°方向，SLVL＝－40dB，NLVL＝－90dB，在64°、70°和76°三个位置形成零陷。

在这里不整编码等分数m＝1 000，其他参数保持不变。在经过1 000次迭代后，优化结果如下：其阵元的电流激励幅度依次为0.923，0.870，0.789，0.691，0.557，0.442，0.322，0.216，0.104，0.70，得到的最大副瓣电平为－39.457dB，3处零陷中绝对值最小的零陷深度为－91.519dB，比文献［13］中的最大副瓣电平和零陷深度分别降低了2.800 2dB和2.308 3dB，方向图如图4所示。

［例4］设计指标：n＝10，即天线的阵元个数为20个，阵元间距d＝0.5λ，主瓣对准90°方向，SLVL＝－15dB，NLVL＝－95dB，在30°、40°、50°、60°和70°位置形成零陷。

由于需要优化的零陷个数较多，优化问题的复杂度较高。为了提高算法的搜索精度，令m＝10 000，ant＝100.在经过100次迭代后，优化结果如下：其阵元的激励幅度依次为0.737 7，0.733 6，0.728，0.595 9，0.652 1，0.615 8，0.472 4，0.235 2，0.398 5，0.069 6，得到的各个角度的零陷深度均在－95dB以下，而且其最大副瓣电平为－20.044 dB，比文献［14］中同样采用100个粒子100次迭代的粒子群优化（PPSO）算法优化的最大副瓣电平降低了2.213dB.其方向图如图5所示。

4.结 论

采用改进型蚁群算法，通过优化天线阵元的电流激励幅度，完成天线阵方向图综合，效果良好，计算结果表明其优化结果优于遗传算法和粒子群算法。改进型蚁群算法，通过加入不整编码和邻域优化，比传统的蚁群算法更适合于连续函数的优化，并且不容易陷入局部最优，收敛速度较快，为解决多变量连续函数优化问题提供了一种新思路新方法。

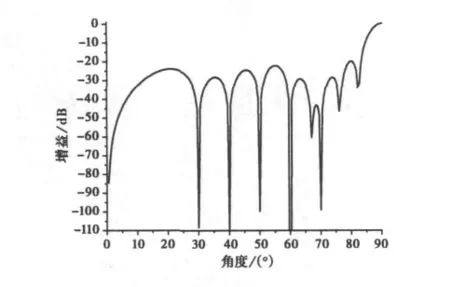
图5 0.5λ间距30°、40°、50°、60°和70°方向形成零陷的优化方向图

［1］赵瑞峰，谈振辉，蒋海林.无线系统中的智能天线［J］.电子学报，2000，28（12）：78－80.ZHAO Ruifeng，TAN Zhenhui，JIANG Hailin.Smart antennas for wireless systems［J］.Acta Electronica Sinica，2000，28（12）：78－80.（in Chinese）

［2］MAILLOUX R J.相控阵天线手册［M］.北京：电子工业出版社，2006：88－98.

［3］COLORNI A，DORIGO M，MANIEZZO V，et al.Optimization by a colony of cooperating agents［J］.IEEE Transactions on Systems，Man and Cybernetics－Part B，1996，26（1）：1－13.

［4］DORIGO M，GAMBARDELLA L M.Ant colony system：a cooperative learning approach to the traveling salesman problem［J］.IEEE Trans on Evolutionary Computing，1997，1（1）：53－56.

［5］COLORNI A，DORIGO M，MANIEZZO V.Ant colony system for job－shop scheduling［J］.Begian J of Operations Research Statistics and Computer Science，1994，34（1）：39－53.

［6］段海滨.蚁群算法原理及其应用［M］.北京：科学出版社，2005：24－42.

［7］SCAR Q，EVA R.Ant colony optimization in thinned array synthesis with minimum sidelobe level［J］.IEEE Antennas and Wireless Propagation Letters，2006，5（1）：349－352.

［8］任盛海，吴志忠.遗传算法在阵列天线方向图综合设计中的应用［J］.电波科学学报，1996，11（4）：62－67.REN Shenghai，WU Zhizhong.Application of genetic algorithms in the synthetic design for the radiation pattern of an array antenna［J］.Chinese Journal of Radio Science，1996，11（4）：62－67.（in Chinese）

［9］马云辉.阵列天线的遗传算法综合［J］.电波科学学报，2001，16（2）：172－176.MA Yunhui.Synthesis of the array antennas using genetic algorithm［J］.Chinese Journal of Radio Science，2001，16（2）：172－176.（in Chinese）

［10］范 瑜，金荣洪.基于一种新的遗传算法的天线方向图综合技术［J］.电波科学学报，2004，19（2）：182－186.FAN Yu，JIN Ronghong.Pattern synthesis of antennas based on a novel genetic algorithm［J］.Chinese Journal of Radio Science，2004，19（2）：182－186.（in Chinese）

［11］HU XIAOMIN，ZHANG JUN，CHUNG H S H，et al.SamACO：variable sampling ant colony optimization algorithm for continuous optimization［J］.IEEE Transactions on Systems，Man，and Cybernetics.2010，40（6），1555－1566.

［12］KENNEDY J，EBERHART R C.Particle swarm optimization［C］//Proc of Sixth International Conference on Neural Networks.Perth，Australia，1995：1942－1948.

［13］尚 飞，蔡亚星，张 颖，等.阵列天线的双种群遗传算法综合［J］.电波科学学报，2007，22（2）：224－228.SHANG Fei，CAI Yaxing，ZHANG Ying，et al.Synthesis of array antenna using double population genetic algorithm［J］.Chinese Journal of Radio Science，2007，22（2）：224－228.（in Chinese）

［14］金荣洪，袁智皓，耿军平，等.基于改进粒子群算法的天线方向图综合技术［J］.电波科学学报，2006，21（6）：873－878.JIN Ronghong，YUAN Zhihao，GENG Junping，et al.The pattern synthesis of antennas based on a modified PSO algorithm［J］.Chinese Journal of Radio Science，2006，21（6）：873－878.（in Chinese）

［15］丁永生.计算智能理论技术与应用［M］.北京：科学出版社，2004：144－145.