弹载合成孔径雷达动态海面成像模拟研究
祝明波 邹建武 董 巍 谢 飞
(1.海军航空工程学院,山东 烟台264001;2.海军航空管制设备维修中心,北京100071)
引 言
合成孔径雷达(SAR)具有高分辨力成像、全天时、全天候工作等特点。利用弹载SAR作为传感器进行成像制导是目前精确制导技术的一个重要发展方向。性能分析是弹载SAR成像制导的首要问题,一种简便、有效的方法就是利用系统仿真进行研究。文中以反舰导弹应用为背景,主要关注海面(舰船目标背景)的高逼真模拟及其快速实现。
公开发表的有关弹载SAR动态海面成像模拟的文献极少,只有少量星载和机载条件下对海洋进行遥感的相关文献。对海面进行SAR成像模拟是研究海面成像机制的一种重要手段,目前主要有两种方法可用于海面的SAR成像模拟[1-4]。一是根据海面的几何模型、电磁散射模型和成像模型(如速度聚束模型)直接仿真得到SAR图像。2002年,王爱明等研究了星载SAR对海面波成像的机理和海面波对雷达截面的调制机理,选用速度聚束模型,在不同参数下,利用SAR对海面波进行了成像模拟[1];2009年,赵志钦等基于海面模型、电磁散射模型以及海面成像机制等理论模型对海面进行成像模拟得到了海面的极化SAR图像[2],该方法运算量较少,但不能较全面的反映SAR系统特征。二是通过仿真海面的SAR回波间接得到SAR图像。1998年,G.Franceschetti在常规SAR回波生成的基础上,通过坐标变换得到海面场景SAR回波[3];2007年,王敏通过产生时序的回波开展了星载SAR条件下的海面成像模拟[4],此方法模拟效果较好,但运算量较大。
上述两种方法都涉及海面电磁散射理论,目前,有关海面的散射理论主要有两大类:解析近似方法和数值方法。数值方法实现起来较为复杂且计算量大,我们主要讨论解析近似方法。常用的近似方法:基尔霍夫(Kicrhhoff)近似法、微扰法和双尺度方法。Kicrhhoff近似法主要考虑低入射角下镜面散射机制,微扰法主要考虑布拉格散射机制,双尺度法则同时考虑镜面散射和布拉格散射。利用近似方法所建立的常用海面电磁散射模型有布拉格散射模型、光学散射模型和双尺度散射模型[5-8]。
通过生成时序海面回波的方法,在弹载SAR平台情况下,对动态海面成像模拟进行了系统研究。出于逼真性及运算速度考虑,且便于后续的弹载SAR成像制导系统的性能分析,在合适的三维动态海面模型、海面电磁散射模型、海面场景回波模型和雷达实时工作过程的基础上,提出了基于三维海面波动模型及弹载SAR工作过程的成像模拟方案。结合一组典型弹载SAR系统参数,分别在正侧视和斜视工作模式下对三种典型海况的动态海面进行了成像模拟,并利用实际海面SAR图像的统计特性对模拟结果的有效性进行了检验。
1.动态海面SAR成像模拟方案
与陆地静态场景不同,海面场景的SAR成像模拟涉及到的新问题主要表现在海面及其电磁散射是动态变化的。如前所述,目前SAR成像模拟主要有两种方法:第一种方法运算量较少,但涉及到不同的海面成像模型,不能较全面反映SAR系统特征;第二种方法不依赖具体的成像模型,并且对不同成像条件下海面成像效果的分析及对于对海成像弹载SAR系统的优化设计具有明显优势,但运算量较大。针对反舰导弹弹载SAR成像制导海面背景仿真及后续性能分析的需要,出于逼真性考虑,在第二种模拟方法的基础上,提出了基于海面波动模型及弹载SAR工作过程的成像模拟方案,主要分为四个步骤:
1)三维动态海面的几何模型的建立。目前主要有如下五种海面建模方法:基于流体力学的建模方法、基于海浪谱的建模方法、基于几何造型的建模方法、基于动力模型的建模方法和基于分形的建模方法。出于逼真性及运算速度的考虑,选用基于海浪谱的双尺度海面模型[9-12]。
2)海面电磁散射模型的建立。鉴于海面是由大的波浪及覆盖在其上的小的风浪和毛细波组成的,可简化为仅含有两种尺度粗糙度的表面,因此,适合选用双尺度散射模型进行建模。
3)建立动态海面的回波信号模型。首先,建立海面电磁散射模型,求解每个小面的后向散射系数。根据SAR的运动轨迹、SAR系统的参数与成像模式,建立SAR动态海面的回波信号模型。
4)弹载SAR动态海面成像模拟。在生成海面场景回波的基础上,利用不同模式下的成像算法对海面进行成像模拟。
需要指出的是,方案中的最后三个步骤与导弹的飞行弹道[13]及弹载SAR的工作模式密切相关,为简化分析与仿真,假设导弹采用低空平直弹道,弹载SAR工作于正侧视和斜视模式。
2.双尺度海面模型
建立三维动态海面的几何模型是弹载SAR动态海面成像模拟最基础也是最重要的一步。
对于通常海面而言,海浪的波高一般能达到数英尺,并且在大的波浪上面还覆盖着小的风浪和毛细波,即由大尺度的重力波和小尺度的张力波组成。重力波的时间标度从0.1s到25s,波长从2cm到500m,高度可达30m,其主要回复力为重力。重力波一般处于两种状态:风浪(sea)和涌浪(swell)。表面张力波提供了海面的精细结构,其时间标度从0.01s到0.1s,波长从0.5cm到2cm,高度小于1cm,主要回复力是表面张力。建模时,可将海面简化为仅含有两种尺度波浪的表面:大尺度波表面和小尺度波表面,也就是所谓的双尺度海面模型。
双尺度海面模型中大尺度波的海浪谱选用Fung完全海谱[12]中的S1(k),小尺度波的海浪谱选用Fung完全海谱中的S2(k)。Fung完全海谱是建立在P-M谱与Pierson提出的张力波谱的基础上的。k为波数,当k<0.04rad/cm时应用重力波谱,当k>0.04rad/cm时应用张力波谱,并令k=0.04 rad/cm时二者谱密度相等,从而得到一种完全谱。S1(k)和S2(k)定义如下:

式中:α为谱相关系数,值为5.6×10-3;gc是重力加速度,值为9.81m/s2;U19.5为海面19.5m 处的风速。
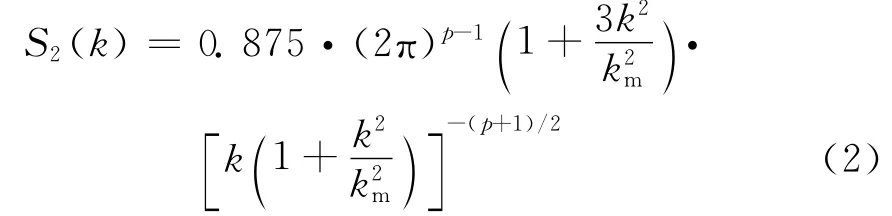
式中:km=3.63rad/cm;p=5-lg(U*),U*是摩擦风速,单位为cm/s.设已知高度为z的风速为U,则U与U*之间的关系可以表示为
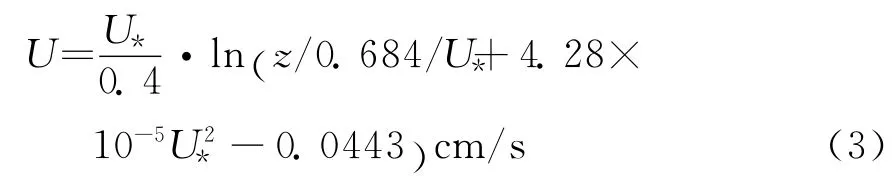
总的双尺度海面的海浪谱可以表示为

利用双尺度海面海浪谱仿真出的某一时刻的海面如图1~3所示。此处风速为高出海面10m处的风速,风速为3m/s、10m/s和20m/s的情况,分别对应着低海况、中海况和高海况下的典型海面。
3.双尺度电磁散射模型
由于海面是分布面目标,海面电磁散射模型所求的是归一化雷达截面。双尺度法是在Kirchhoff近似和微扰法的基础上发展起来的[14]。双尺度法考虑小尺度布拉格散射占优的散射机制,以及大尺度对小尺度调制。双尺度模型同时考虑了Kirchhoff散射模型和微扰(布拉格)模型,形成所谓的组合粗糙表面散射模型,该散射模型与双尺度海面模型相呼应。考虑二维动态离散海面z[x(m),y(n),t],其中,x,y方向的离散点数分别为M,N,由双尺度模型,HH极化的后向散射系数为

VV极化的后向散射系数为
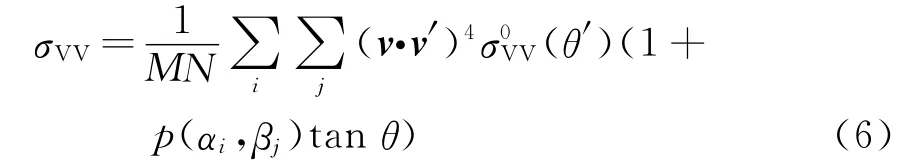
式中:h,v,h′,v′分别为基准坐标系xyz和本地坐标系x′y′z′中的单位水平极化矢量和单位垂直极化矢量;θ和θ′分别为入射角和本地入射角;αi和βj分别表示某粗糙面元x方向和y方向的斜率变量;p(αi,βj)为小面单元在电磁波入射方向的斜率;(θ′)和(θ′)分别为本地坐标系下小扰动法求得的散射系数:
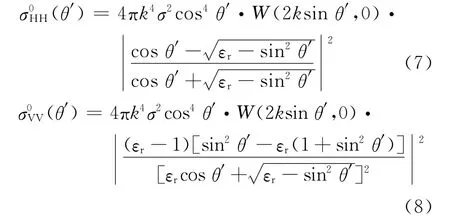
式中:k为电磁波数;σ2为海表面的高度起伏均方差;εr为海水的相对介电常数,W(2ksinθ′,0)为小尺度波数谱。
上述双尺度散射模型是针对某一区域海面后向散射系数平均值,就单个小面单元而言,其后向散射系数为

4.海面场景回波模型
简单起见,此处以正侧视为例介绍海面场景回波模型。
通常SAR发射的信号是线性调频脉冲串,可表为
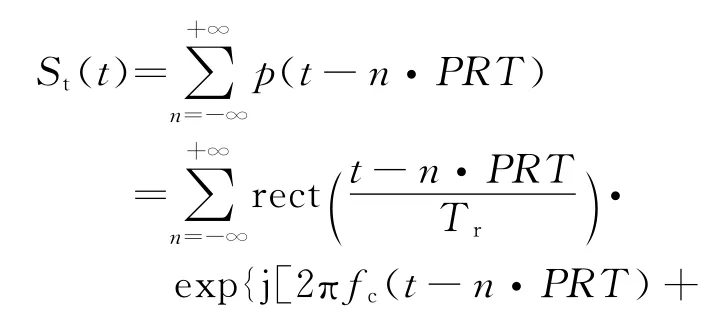
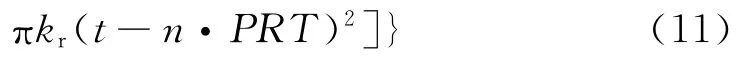
式中:rect(·)为矩形窗函数;fc为载频;kr为线性调频率;PRT为脉冲重复周期;Tr为脉冲持续时间。
弹载SAR的工作过程:雷达以一定的PRT发射和接收线性调频脉冲,在脉冲持续期间,Tr为μs量级,此时海面波动很小,可忽略其变化,将海面上各点目标的雷达散射截面视为定值。而在弹载SAR脉冲重复期间,PRT为ms量级,海面变化相对较大,海面各点的雷达散射截面亦随之变化。天线波束照射到海面上近似为一矩形区域,区域内各散射元(点)对入射波后向散射,发射脉冲经过目标和天线方向图的调制,携带目标和环境信息形成SAR回波。从时域来看,发射和接收的信号都是一时间序列。
设雷达发射信号为线性调频脉冲,则单个海面小平面单元回波信号可写成
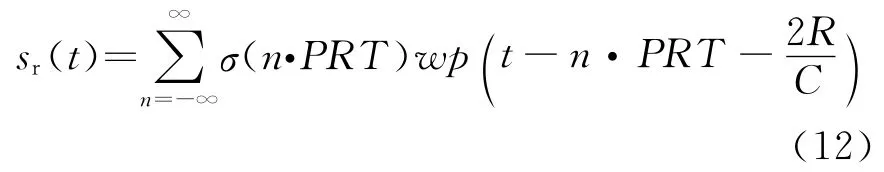
式中:σ(n·PRT)为n·PRT时刻的点目标的雷达散射截面;w表示点目标天线方向图双向幅度加权;R为小面单元到雷达相位中心的瞬时斜距。
海面场景回波模拟流程如图4所示。
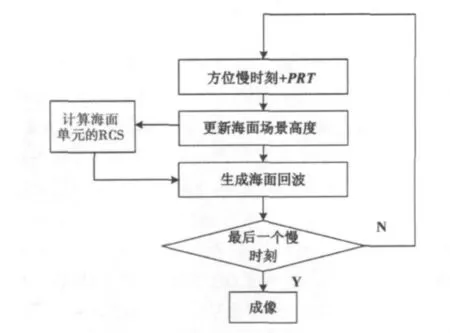
图4 海面场景回波模拟流程
5.模拟结果及效果评价
5.1 成像模拟结果
参考国外几种典型小型SAR系统的性能指标[15]选取正侧视模式下弹载SAR系统参数如表1所示。

表1 SAR系统参数
为反映不同海况对成像的影响,分别对高出海面10m处的风速为3m/s、10m/s和20m/s的双尺度动态海面进行了成像模拟。海面方位向范围:0~300m,海面距离向范围:0~100m.模拟结果如图5~图7所示。所有SAR图像的横向为方位向,纵向为距离向。
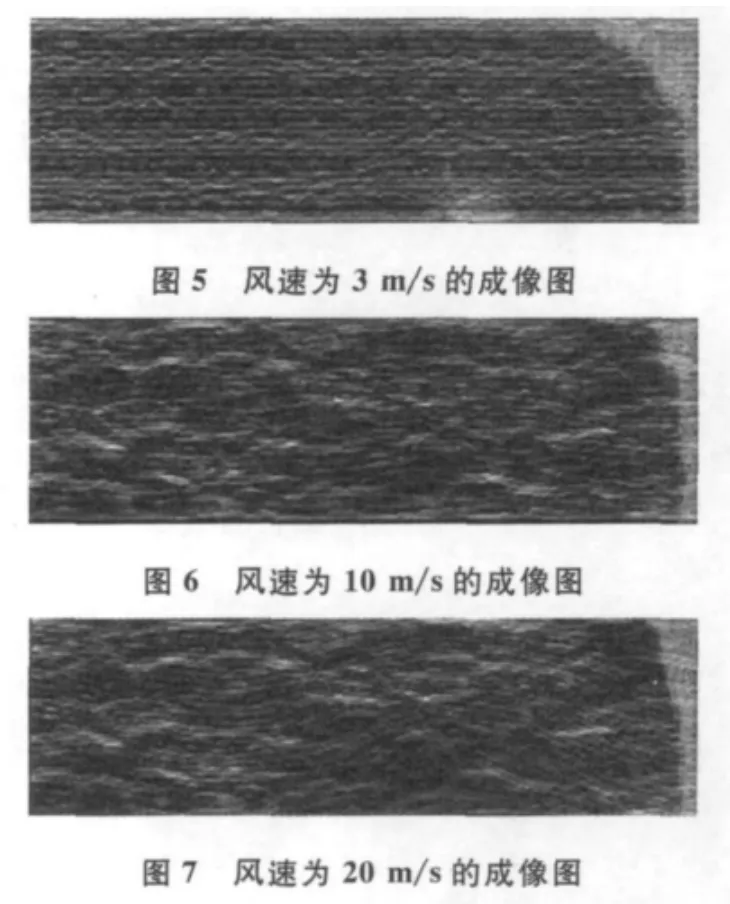
斜视模式下,除入射角为64.34°,斜视角为30°,其他参数相同。海面方位向范围:0~120m,距离向范围:0~120m.模拟结果如图8(a)、图9(a)和图10(a)所示。
5.2 模拟结果评价
由于雷达分辨率的提高,将导致在分辨单元内以后向散射电磁能量表征的海面回波幅度的降低,在低振幅段的概率极大,从而概率密度函数呈现出非对称尖峰特征。描述这些特征的概率密度函数类型很多,如K分布、对数正态分布、韦伯尔分布、广义K分布等[16],通过对真实海洋SAR图像数据分析表明,K分布是描述SAR回波比较好的概率模型[3],K分布的概率密度函数为


式中:随机变量z>0;v>0为形状参数,v越小K分布的曲线越尖锐;a>0为尺度参数;Γ(·)是Gamma函数;Kv-1(·)是第二类修正的Bessel函数。
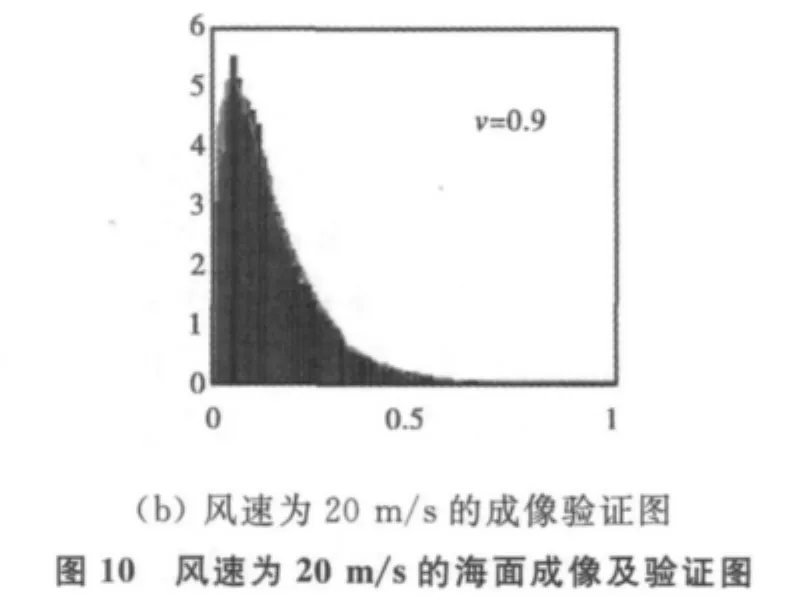
采用归一化灰度直方图对斜视角为30°成像模式下不同风速下的弹载SAR动态海面模拟图像进行了检验,结果如图8(b)、图9(b)和图10(b)所示。结果表明:所模拟的图像幅度与K分布拟合很好,符合实际海面SAR图像的统计特性;且海况越高,K分布形状参数越小,反映此时幅度分布偏离瑞利分布的程度越大,这与实际海面场景SAR图像的统计特性相一致。
6.结 论
主要研究了弹载平台下SAR对海成像的模拟,出于逼真性及运算速度的考虑,提出了基于三维海面波动模型及弹载SAR工作过程的成像模拟方案。着重介绍了基于海浪谱的海面建模方法,并利用双尺度海面模型仿真出了所需要的海面。利用双尺度电磁散射模型,构造了海面场景回波模型。对三种海况下的动态海面在正侧视和斜视模式下进行了成像模拟,采用归一化灰度直方图对海面SAR成像模拟结果进行了检验,结果表明,所模拟的图像与实际海面场景SAR图像的统计特性相一致,验证了方案的有效性和结果的逼真性。
[1]王爱明,朱敏慧,康雪艳,等.海面波合成孔径雷达成像仿真研究[J].测试技术学报,2002,16(3):157-161.WANG Aiming,ZHU Minhui,KANG Xueyan,et al.The simulation study of ocean surface wave imaging by SAR[J].Journal of Test and Measurement Technology,2002,16(3):157-161.(in Chinese)
[2]赵志钦,骆小谚,聂在平.利用双尺度模型的海浪极化SAR成像模拟[J].电子科技大学学报,2009,38(5):651-655.ZHAO Zhiqin,LUO Xiaoyan,NIE Zaiping.Simulation of polarization SAR imaging of sea wave using twoscale model[J].Journal of University of Electronic Science and Technology of China,2009,38(5):651-655.(in Chinese)
[3]FRANCESCHETTI G,MAURIZIO M,RICCO D.On ocean SAR raw signal simulation[J].IEEE Trans on GRS,1998,36(1):84-100.
[4]王 敏,何志华,董 臻,等.星载SAR海面场景回波仿真[J].信号处理,2008,24(5):835-838.WANG Min,HE Zhihua,DONG Zhen,et al.Space borne SAR raw signal simulation of ocean scene[J].Signal Processing,2008,24(5):835-838.(in Chinese)
[5]郭立新,王 蕊,吴振森.随即粗燥面散射的基本理论与方法[M].北京:科学出版社,2010:77-82.
[6]杨 超,郭立新.高斯介质粗糙面电磁散射的小斜率近似方法[J].电波科学学报,2009,24(1):77-82.YANG Chao,GUO Lixin.Electromagnetic scattering from Gaussian dielectric rough surface using small slope approximation method[J].Chinese Journal of Radio Science,2009,24(1):77-82.(in Chinese)
[7]吴振森,衣方磊.一维动态海面的电磁散射杂波模拟和参数估计[J].电波科学学报,2003,18(2):132-137.WU Zhensen,YI Fanglei.Numerical simulation and parameters estimation of scattering clutter from 1-D timevarying sea surface[J].Chinese Journal of Radio Science,2003,18(2):132-137.(in Chinese)
[8]FUNG A K,LEE K K.A semi-empirical sea-spectrum model for scattering coefficient estimation[J].IEEE Journal of Oceanic Engineering,1982,7(4):166-176.
[9]邱 捷,陈雷霆.基于物理模型的实时海面模拟[J].计算机学报,2006,34(1):4-7.QIU Jie,CHEN Leiting.Real time ocean simulation based on physical ocean model[J].Computer and Digital Engineering,2006,34(1):4-7.(in Chinese)
[10]FOSTER N,METAXAS D.Modeling water for computer animation[J].Commun ACM,2000,43(7):60-67.
[11]李 晖,郭 晨,李晓方.基于虚拟现实技术的不规则海浪三维仿真[J].大连海事大学学报,2004,30(1):5-8.LI Hui,GUO Chen,LI Xiaofang.3.3-D visual simulation of irregular ocean waves based on virtual reality[J].Journal of Dalian Maritime University,2004,30(1):5-8.(in Chinese)
[12]POZZER C T,ROBERTO S,PELLEGRINO M.Procedural solid-space techniques for modeling and animating waves[J].Computer and Graphics,2002,26(6):877-885.
[13]颜仲新,刘鼎臣,胡 海.反舰导弹飞行弹道探讨[J].飞航导弹,2002(2):33-36.
[14]ULAHY F T.Microwave Remote Sensing[M].Boston:Addison Wesley Publishing,1982:311-322.
[15]董 巍.弹载合成孔雷达成像匹配制导参考图制备技术研究[D].烟台:海军航空工程学院,2009:31-32.DONG Wei.Reference Map Generation Techniques for Image Matching Guidance with Missile-borne SAR[D].Yantai:Naval Aeronautical Engineering Institute,2009:31-32.(in Chinese)
[16]扈罗全,林乐科,朱洪波.三种重拖尾分布海杂波的比较与分析.电波科学学报,2007,22(6):75-78.HU Luoquan,LIN Leke,ZHU Hongbo.Comparison and analysis of three kinds of distribution of sea clutter with heavy tails[J].Chinese Journal of Radio Science,2007,22(6):75-78.(in Chinese)

