低快拍下多输入多输出雷达中的角度估计算法

李建峰 张小飞

（南京航空航天大学电子信息工程学院；江苏 南京210016）

引 言

多输入多输出（MIMO）雷达用多个天线同时发射信号，用多个天线接收反射回的信号，跟传统相控阵雷达相比，有很多优点［1－5］。相比单个发射天线，MIMO雷达拥有更多的自由度，可以克服衰落效应，提高空间分辨率，增强参数识别能力和提高目标侦测性能［6－10］。目前，MIMO雷达中已经有很多离开角（DOD）和波达角（DOA）估计算法，包括借助旋转不变技术的信号参数估计（ESPRIT）方法［11］，Capon方法［12］，多重信号分类 （MUSIC）方法［13］，平行因子算法［14］以及自适应平行因子方法［15］等，以上算法在比较高的快拍数下，能获得较好的性能，而在较低的快拍下，性能就会变得很差。文献［16］提出了一种单快拍数下双基地MIMO雷达的角度估计算法，该算法需要两个一维谱搜索估计，复杂度高；还需要额外的参数配对。为此，文中提出了低快拍下的MIMO雷达中一种低复杂度、自动配对的角度估计算法，该算法利用矩阵束（Matrix Pencil）方法来实现DOD和DOA的较准确的联合估计，通过构造矩阵，能实现甚至在单快拍下的角度估计，算法复杂度低于ESPRIT算法，且估计的角度能自动配对；同时，论文中所提算法的角度估计性能好于ESPRIT算法。

1.理论分析

1.1 数据模型

考虑双基地MIMO雷达中，发射阵列M元的均匀线阵（ULA），接收阵列为N元的ULA，阵元间隔半波长。假设有D个不相关的目标，则接收端匹配滤波器的输出为

式中：θd，ød分别是第d个目标对应于发射阵列的DOD和对应于接收阵列的，i为虚部符号；fd为多普勒频移；βd是反射系数，不同目标之间不相关，（·）T表示矩阵转置；n（t）是MN×1的高斯噪声向量，均值为0，协方差矩阵为σ2IMN，IMN是MN×MN的单位矩阵；ar（ød）⊗at（θd）是对应于第d个目标的发射方向矢量和接收方向矢量的Kronecker积，其中

式中exp（－iπ）代表e－iπ.

式中：N∈CMN×J是噪声矩阵；B＝［b（1），b（2），…，b（J）］∈CD×J.

无噪声时，X的第（（n－1）M＋m）行为

式中bd是B的第d行。定义

式中E［·］代表求期望；（·）H表示矩阵的共轭转置。忽略多普勒频移影响，则

式中ad＝bd.利用式（6）构造增广矩阵

其中

Rm为Q×（N－Q＋1）的Hankel矩阵，将式（7）代入式（9），得

式中：

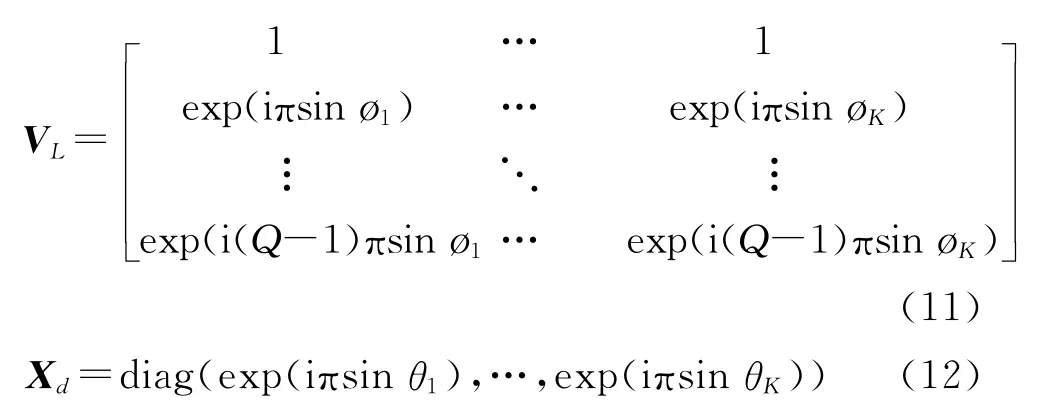
式中diag（v）表示一个对角矩阵，其对角元素为v.

将式（10）代入式（8），得到

式中：

1.2 基于矩阵束的角度估计算法

1.2.1 DOA估计

对Re进行奇异值分解，得到

式中：Usa、Dsa为包含信号子空间的D个主特征向量与主特征值；Una、Dna分别包含其他特征值与特征向量。由于EL与Usa张成相同的信号子空间，因此，存在唯一K×K的非奇异矩阵T1，使得

根据式 （15），定义

式中：Ua1表示由信号特征向量矩阵Usa的前（P－1）Q行构成的矩阵；Ua2表示由信号特征向量矩阵Usa的后（P－1）Q行构成的矩阵；E1表示由信号特征向量矩阵EL的前（P－1）Q行构成的矩阵。由式（18）得

定义Fa＝Ua2，其中（·）＋表示矩阵的广义逆。对Fa进行特征值分解，对应的特征矢量则达到T1的估计

式中，Π为列交换矩阵，而且Π－1＝ΠT，其中（·）－1表示矩阵求逆。所以在无噪声情况Xd的估计

假设对Fa进行特征值分解得到特征值，则DOA的估计为

式中angle（·）表示取相位。

1.2.2 DOD估计

通过对EL左乘一个置换矩阵，得到

式中：

用此置换矩阵乘以Usa，可得

同理，定义

式中：Ud1表示由信号特征向量矩阵Usd的前（Q－1）P行构成的矩阵；Ud2表示由信号特征向量矩阵Usd的后（Q－1）P行构成的矩阵；E1C表示由信号特征向量矩阵ELC的前（Q－1）P行构成的矩阵。由式（24）得

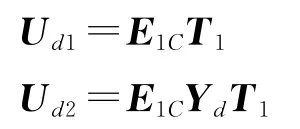
则

因为Yd＝（E1CYd），可以通过下式得到Yd的估计

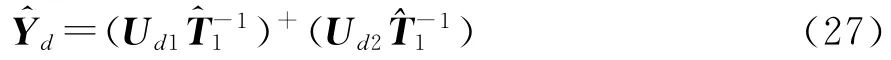
假设估计出的Yd的对角元素为，则DOD的估计为

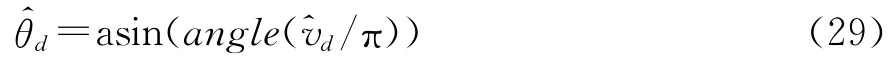
至此，将此基于矩阵束的角度估计算法流程总结如下：

1）根据接收数据通过式（6）构造r（τ，ζ）；

2）选择合适的P值和Q值（注1），构造出式（8）中的Re和式（9）中的Rm；

3）对Re进行奇异值分解，取其左奇异向量Usa的前（P－1）Q行Ua1，后（P－1）Q行Ua2，并对Ua2特征值分解，得到特征值，根据公式（22＝asin（angle）/π），从特征值中得到 DOA 的估计，根据式（20）从特征矢量得到T1的估计；

4）将Usa左乘一置换矩阵进行重构，得到Usd，并取其前（Q－1）P行Ud1，后（Q－1）p行Ud2，根据式（27）得到Yd的估计，并取其对角元素得到，再根据式（29＝asin（angle/π）），得到DOD的估计

注1：P，Q的选取应满足M－D＋1≥P≥D＋1，N－D＋1≥Q≥D＋1；P，Q的选取，旨在构造增广矩阵，相当于增大快拍数，使角度估计在低快拍下也能获得很好的性能。构造增广矩阵之后，由公式（11）～（17），可以把Q看成新的接收阵列长度，把P看成新的发射阵列长度。注2：根据公式（21）和（28），我们发现估计出DOD和DOA具有相同的列模糊，所以该算法能自动进行二维角度配对。

1.2.3 复杂度及克拉美－罗界（CRB）

根据文献［17］，可以给出双基地MIMO雷达中的CRB为

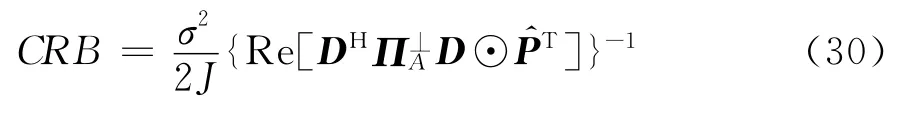
2.实验结果分析

2.1 仿真结果及分析

图1和图2给出了在M＝8，N＝8，J＝4，信噪比（SNR）分别为0dB，4dB的情况下，该算法的角度估计性能，从图1和图2中可以看出：即使在很低的快拍数下，很低的信噪比下，目标角度都可以被较准确地估计出来。

图3和图4则是M＝8，N＝8，J＝4和M＝8，N＝10，J＝1的情况下，该算法与ESPRIT算法以及CRB的比较，可以看到文中所提算法的RMSE和CRB比较接近，而在J＝1的情况下，ESPRIT算法已失去估计能力，所提算法依然可以准确估计出角度，所提算法的角度估计性能优于ESPRIT算法，而此时ESPRIT算法的复杂度为O（520 704），所提算法复杂度为O（832 8），远低于ESPRIT算法复杂度。

图5和图6给出了J＝4，发射和接收天线数不同的情况下，该算法的估计性能。可以看出：随发射和接收天线数增加，估计性能提升。天线数增加，分集增益增强，性能得到提升。

图7则是M＝8，N＝8，快拍数不同的情况下，算法的估计性能。从图7中可以看出：快拍数增加，估计性能有所提升。

2.2 算法优点

至此，将此基于矩阵束的角度估计算法的优点总结如下：

1）该算法无需谱峰搜索，而且其复杂度低于ESPRIT算法；

2）在低快拍情况下论文中所提算法的角度估计性能优于ESPRIT算法；

3）该算法能工作在单快拍下；

4）该算法能对二维角度自动配对。

3.结 论

文中提出了双基地MIMO雷达中的一种低快拍低信噪比下的DOD和DOA联合估计算法。该算法利用矩阵束方法构造矩阵，通过奇异值分解和ESPRIT方法获得角度信息。该算法估计的角度能自动配对，无需谱峰搜索，复杂度低于传统的ESPRIT算法，而且其角度估计性能在低快拍下优于传统ESPRIT算法。一系列仿真验证了该算法的有效性。

［1］FISHLER E，HAIMOVICH A，BLUM R S，et al.MIMO radar：an idea whose time has come［C］//Proc IEEE Radar Conf，26－29April，2004：71－78.

［2］LI J，STOICA P.MIMO radar－diversity means superiority［C］//Proceeding of 14th Annual Workshop A－daptive Sensor Array Processing Workshop.Lexington，December 2006：201－207.

［3］LI X，ZHANG Z，et al.A study of frequency diversity MIMO radar beamforming［C］//IEEE 10th International Conference on Signal Processing.Beijing，24－28October，2010：352－356.

［4］SHARMA R.Analysis of MIMO radar ambiguity functions and implications on clear region［C］//IEEE Radar Conf，June 2010：544－548.

［5］刘晓莉，廖桂生.多基线数据融合的双基地MIMO雷达角度估计［J］.电波科学学报，2010，25（6）：1199－1205.LIU Xiaoli，LIAO Guisheng.Angle estimation based on multibaseline data fusion for bistatic MIMO radar［J］.Chinese Journal of Radio Science，2010，25（6）：1199－1205.（in Chinese）

［6］LI J，LIAO G，GRIFFITHS H.Bistatic MIMO radar space－time adaptive processing［C］//2011IEEE International Radar Conference.Kansas，Missouri，May 2011：498－502.

［7］WU X H，KISHK A A，GLISSON A W.MIMOOFDM radar for direction estimation［J］.IET Radar，Sonar ＆ Navigation，2010，4（1）：28－36.

［8］LI J，STOICA P，XU L，et al.On parameter identifiability of MIMO radar［J］.IEEE Signal Process Lett，2007，14（12）：968－971.

［9］LI J，LIAO G，MA K，et al.Waveform decorrelation for multitarget localization in bistatic MIMO radar systems［C］//2010IEEE International Radar Conference.Washington，May 2010：21－24.

［10］李树峰，张履谦，陈 杰，等.基于完全互补序列的正交MIMO雷达二维DOA估计［J］.电波科学学报，2010，25（4）：617－624.LI Shufeng，ZHANG Lvqian，CHEN Jie，et al.Two－di－mensional DOA estimation for orthogonal MIMO radar based on complete complementary sequence［J］.Chinese Journal of Radio Science，2010，25（4）：617－624.（in Chinese）

［11］CHEN Jinli，GU Hong，SU Weimin.Angle estimation using ESPRIT without pairing in MIMO radar［J］.Electron Lett，2008，44（24）：1422－1423.

［12］YAN H，LI J，LIAO G.Multitarget identification and localization using bistatic MIMO radar systems［J］. EUR－ASIP J Adv Signal Process，2008：283483.

［13］GAO X，ZHANG X，FENG G，et al.On the MUSIC－de－rived approaches of angle estimation for bistatic MIMO radar［C］//International Conference on Wireless Net－works and Information Systems.Shanghai，28－29December，2009：343－346.

［14］ZHANG X，XU Z，XU L，et al.Trilinear decompositionbased transmit angle and receive angle estimation for multiple－input multiple－output radar［J］.IET Radar，Sonar ＆ Navigation，2011，5（6）：626－631.

［15］NION D，SIDIROPOULOS N D.Adaptive algorithms to track the PARAFAC decomposition of a third－order tensor［J］.IEEE Transaction on Signal Process，2009，57（6）：2299－2310.

［16］郑志东，牛朝阳，张剑云.单快拍数下双基地MIMO雷达的角度估计［J］.信号处理，2010，26（5）：789－794.ZHENG Zhidong，NIU Zhaoyang，ZHANG Jianyun.Receiver and transmitter angle estimation for bistatic MIMO Radar with single snapshot［J］.Signal Processing，2010，26（5）：789－794.（in Chinese）

［17］STOICA P，NEHORAI A.Performance study of condi－tional and unconditional direction－of－arrival estimation［J］.IEEE Trans Signal Process，1990，38（10）：1783－1795.

［18］曾建奎，何子述.慢起伏目标的多输入多输出雷达监测性能分析［J］.电波科学学报，2008，23（1）：158－162.ZENG Jiankui，HE Zishu.Analysis of MIMO detection performance for slow fluctuating target［J］.Chinese Journal of Radio Science，2008，23（1）：158－162.（in Chinese）