关于抑制大气湍流对鬼成像的影响研究

杨 华，李永强，郑芝芳

（南京邮电大学 通信与信息工程学院 210003）

0 引言

量子成像，又称“鬼成像”或者关联成像，上世纪80年代，前苏联学者Klyshko根据自发参量下转换光子对的纠缠行为，提出鬼成像方案[1]。1995年，史砚华等人利用自发参量下转换得到的纠缠光子对完成了鬼成像实验[2-3]。实验中将产生的光分成两道光路，一路为信号光路，放有待成像的物体，另一路作为参考光路，不放置任何物体。在信号光路中测量光的强度分布不能得到待成像物体的像，但是通过记录这两条光路的符合计数却可以得到物体的像。鬼成像理论自提出以来，就引起广泛热议和研究。文献[4]很好地阐述了鬼成像的发展过程。

最初对鬼成像的研究都是基于自由空间的光传输，但在实际应用中，光的传输会受到大气湍流等其他因素的影响，进而物体的成像质量也会受到影响。在文献[5-9]中分别对这一现象进行了不同的研究。

本文首先研究大气湍流对纠缠关联成像质量的影响，用随机相位屏模拟湍流对光束相位产生的变化，然后采用纠错编码的方法减小湍流效应。由仿真结果可以看出，对要成像的物体采用简单的线性分组编码之后，成像质量明显提高。

1 大气湍流对鬼成像产生的影响

光在实际传输过程中，在经过大气信道时，大气对激光信号的传输会产生多种形式的影响，例如大气消光导致的光功率降低、大气多次散射导致的激光脉冲时间展宽、光束扩展导致的附加空间损耗、光强闪烁导致的接收光信号起伏等。大气湍流对激光光束的影响程度以及产生的效应与激光光束的直径D及湍流的尺度L（内尺度用l0表示，外尺度用L0表示）有关。

大气中光路的空间变化常用相位屏来模拟，用相位屏模拟激光的传输技术已经被研究了很多年[10]。在本文的仿真中，用相位屏表示大气湍流的存在。折射率功率谱有多种形式，最简单的Kolmogorov谱如下所示：

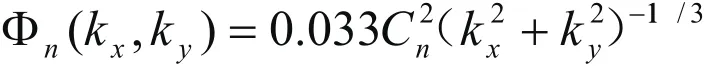
本文选用修正Hill谱密度函数对大气湍流进行计算模拟[10]，如下式所示：

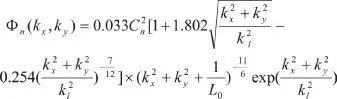
其中Cn2称为大气折射率结构常数，它用于度量光学湍流强度，单位为m-2/3，是湍流强度的重要评价参数。

在仿真中，假设参考光路是理想光路，没有大气湍流的影响，只考虑信号光路中存在大气湍流。在信号光路中，加入相位屏[10]用来模拟湍流的存在，这样就会改变光束的相位，之后再与参考光路进行符合计数，便可得到加入湍流后物体的像。本文利用文献[10]中计算相位屏的公式和折射率功率谱进行模拟仿真。相位频谱如下式所示：

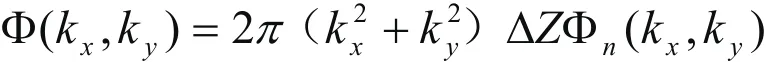
仿真结果如图2(c)所示，可以看到，加入湍流之后NUPT的字样变得模糊。

2 采用（7,4）线性分组码抑制湍流的影响

分组码是一组固定长度的码组，可表示为（n, k），通常它用于前向纠错。在分组码中，监督位被加到信息位之后，形成新的码。在编码时，k个信息位被编为n位码组长度，n-k个监督位的作用是实现检错与纠错。当分组码的信息码元与监督码元之间的关系为线性关系时，这种分组码就称为线性分组码。

对于码组长度为n、信息码元为k位、监督码元为r=n-k位的分组码（常记作（n，k）码），如果希望用r个监督位构造出r个监督关系式来指示一位错码的n种可能，则要求：

2r-1≥或2r≥k+r+1

设分组码（n, k）中k=4，为了能够纠正一位错误，则由上式可以看到要求r≥3，若取r=3，则n=k+r=7 。设本组（7,4）线性分组码信息位和监督位的约束关系为：

c5=c1+c2+c3;

c6=c2+c3+c4;

c7=c1+c2+c4；

由约束关系可以写出生成矩阵G：

利用它可以产生整个码组：

A=CG=[c1 c2 c3 c4]G

C是发送端信息码元，A是编码之后的码元。

由生成矩阵和校验矩阵的关系：

GHT=0

可以得到校验矩阵为：

其中，

P=QT

设接收到的码字为R，定义伴随式

S=RHT

S也叫校正子。

令S’=S mod 2，让H的每一列i依次与S’相加，若和为零矩阵，则表明接收到的R中第i个码字有误，需要进行纠错。例如：C=[1,0,1,1]是要进行编码的信息码字，编码之后变为A=[1,0,1,1,0,0,0]，若接收到的码字为R=[1,0,0,1,0,0,0]，通过计算可以得到S’=[1,1,0],让H的每一列与S’相加之后得到的矩阵为：

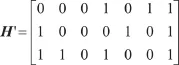
可以看出第3列为零矩阵，说明第三个码字是错误的。纠正之后变为R’=[1,0,1,1,0,0,0]，取前4位就可得到原码字为[1,0,1,1]

根据以上编译码纠错原理，将N*N大小的图进行线性编码，并纠错译码。简单过程如图1所示。

图1 图像编译码过程

先将二维图像转化为一维，然后每4个一组进行线性编码，将编码之后的数据按照鬼成像的理论进行符合计数。由于大气湍流的存在，经过符合计数之后，数值变为小数，不再是0和1，因此，先进行判决，转化为0和1，然后进行纠错译码，最后恢复出原始图像。

3 仿真结果与分析

在本文中，采用LabView软件进行仿真。仿真过程中参数设置如下：湍流内特征尺度l0=0.000 2 m，外特征尺度L0=50 m，折射率结构参数Cn2=5×10-15m-2/3。图2分别是成像的原始图像(a)、未加入湍流的成像结果(b)、加入湍流之后的成像结果(c)，以及进行纠错编码之后得到的成像结果(d)。

图2 仿真结果

由仿真结果可以看出，当信号光路中加入大气湍流时，成像质量明显下降。NUPT的字样变得模糊不清，说明噪声影响很大。但是把图像进行编码译码之后，成像质量得到极大改善，可以完全恢复出NUPT的字样。

4 结论

由于鬼成像是通过信号光路和参考光路的符合计数得到的像，而光在传输过程中存在大气湍流的干扰，因此，本文在信号光路中加入湍流来验证其产生的影响，并采用纠错编码的方法有效抑制了其产生的影响。本文在基于轨道角动量的纠缠关联成像的基础上，用随机相位屏模拟大气湍流的存在，通过具体仿真结果给出说明。由仿真结果可以看出，通过纠错编码可以恢复出被湍流干扰的图像，有效抑制了湍流的影响。

[1]D.N.Klyshko.Photons and Nonlinear Optics[M].New York :Gordon & Breach, 1988.

[2]Pittman TB,Shih YH.Strekalov DV & Sergienko AV,Optical imaging by means of two-photon quantum entanglement [J].Phys. Rev. A.1995:52:3429-3432.

[3]黄蜂.量子纠缠和经典热光的关联成像[J].中国科技信息,2007(16):265-267.

[4]P.B. Dixon, G. Howland,C.Chan,C. O’Sullivan-Hale, B. Rodenburg , D.S. Simon, J.H. Shapiro,A.V. Sergienko,R.W. Boyd, J.C. Howell.Quantum ghost imaging through turbulence[J].Phys. Rev. A 83, 051803(R)(2011).

[5]J.Cheng.Ghost imaging through turbulent atmosphere[J].Optics Express, 2009,17:7916-7921.

[6]C. Li, T. Wang, J. Pu, W. Zhu, R. Rao.Ghost imaging with partially coherent light radiation through turbulent atmosphere[J].Appl. Phys.2010,99:599-604.

[7]D.S.Simon,A.V. Sergienko.Turbulence mitigation in phase-conjugated two-photon imaging[J]. physics.optics, 2011.

[8]Jana D.Strasburg,Warren W. Harper.Impact of atmospheric turbulence on beam propagation[J].Laser Systems Technology II,Proceedings of SPIE, 2004,5413:93-102.