无线激光通信图像去噪技术
翟蓓蓓,孙运强,姚爱琴,赵晓东
(中北大学,仪器科学与动态测试教育部重点实验室, 山西太原 030051)
0 引言
人们利用光通信已经有几千年的历史了,从古代的烽火传递消息,到近代军队的“旗语”,都是光通信的朴素应用;而现代的光纤通信,更是将光通信推向新的高度。光纤通信以其极高的通信码率得到了人们的广泛应用,与微波通信相比,光通信及其灵活的通信方式在某些领域仍有不可替代的作用。而无线激光通信则结合了微波通信和光纤通信的优点。
无线激光通信是涵盖多种领域的综合性技术,其关键技术问题主要有两个方面:一是远距离激光信号的发射与接收技术,其发送和接收信号的距离从上千万米的空间激光通信,到几十千米的地面激光通信;二是激光信号的捕获和自动跟瞄技术。其具体的技术表现在5个方面:(1)光源及
高码率调制技术;(2)大气信道的研究;(3)精密、可靠、高增益的收发天线;(4)高灵敏度抗干扰的光信号接收技术;(5)快速、精确的捕获、跟踪和瞄准技术。
1 图像去噪方法研究
1.1 图像去噪处理
图像去噪声处理从整个图像分析的流程上来讲属于图像的预处理阶段,从数字图像处理的技术角度来说属于图像恢复的技术范畴,它的存在有着非常重要的意义,主要表现在:
(a)由于不同的成像机理,得到的初始图像中都含有大量不同性质的噪声,这些噪声的存在影响着人们对图像的观察,干扰人们对图像信息的理解。噪声严重时候,图像几乎产生变形,更使得图像失去了存储信息的本质意义。显然,对图像进行去噪处理是正确识别图像信息的必要保证。
(b)除了能提高人视觉识别信息的准确性,对图像进行去噪的意义还在于它是对图像作进一步处理的可靠保证。如果对一幅含有噪声的图像进行特征提取、配准或者图像融合等处理其结果肯定不能令人满意,所以图像去噪是必要的。
1.2 图像空间域去噪
邻域平均法是一种局部空间域处理的算法。设一幅图像f(x,y)为对M×N的阵列,处理后的图像为g(x,y)。它的每个像素的灰度值由包含(x,y)邻域的几个像素的灰度值的平均值决定。即用下式得到处理后的图像:
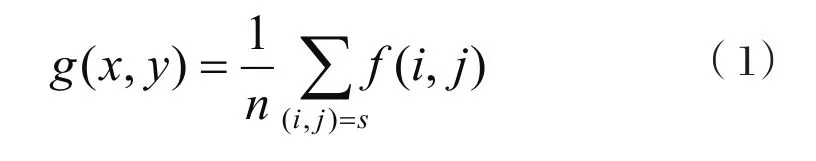
其中1≤x≤M, 1≤y≤N,S是以(x,y)点为中心的领域的集合,n是S内坐标点的参数。

图1 4邻域点(左)和8邻域点(右)的集合
图像邻域平均法的处理效果与所用的邻域半径有关。半径越大,则图像的模糊程度也越大。另外图像邻域平均法算法简单,计算速度快,但它的主要缺点是在降低噪声的同时使图像产生模糊,特别在边缘和图像细节处,邻域越大,模糊越厉害为了减少这种效应,可以采取阈值法,也就是根据下列准则形成处理图像。

其中T是一个规定的非负阈值,当一些点和它们邻值的差值不超过规定的T阈值时,仍保留这些点的像素灰度值。这样处理后的图像比直接采用式(1)的模糊度要小。当某些点的灰度值与各邻点灰度的均值差别较大时,它很可能是噪声,则取其邻域平均值作为该点的灰度值,它的处理效果仍然是很好的。为了克服简单局部平均的弊病,目前已提出许多保留边缘细节的局部平滑算法。它们讨论的重点都在如何选择邻域的大小,形状和方向,如何选择参加平均的点数以及邻域各点的权重系数等。如果将受噪声干扰的图像看成一个二维随机场,则可以运用统计理论来分析受噪声干扰的图像平滑后的信噪比问题。在一般情况下,如果噪声属于加性噪声,并且是独立的高斯白噪声(均值为零,方差为σ2),由信噪比定义为含噪图像的均值与方差之比,则含噪图像经邻域平均法处理后,其信噪比将提高倍(n
为邻域中包含的像素数目)可见邻域取的越大,像素点越多,信噪比提高越多,平滑效果越好。
1.3 图像变换域去噪方法
图像变换域去噪方法是对图像进行某种变换,将图像从空间域转换到变换域,再对变换域中的变换系数进行处理,再进行反变换将图像从变换域转换到空间域来达到去除图像噪声的目的。
频率域低通滤波是基于傅里叶变换的去噪方法。而对于数字化的图像,采用的是二维的离散傅里叶变换。以下是对二维离散傅里叶变换的介绍。
离散傅里叶变换在数字信号处理及数字图像处理中应用十分广泛。它建立了离散空间域和离散频率域之间的联系。
我国历史上迄今保存最为完好的皇家藏书楼是皇史宬。嘉靖十三年(1534年)七月,明世宗效仿古代的“石室金匮”之制,开始在顺天府(今北京)兴建皇史宬。皇史宬用于专门收藏皇帝《宝训》《实录》《玉碟》等皇家典籍与贮存《永乐大典》副本,是我国迄今保存最为完好的皇家藏书楼。
(1) 二维离散傅里叶变换的定义
定义:二维离散信号{f(x,y)x=0,1,…,M-1;y=0,1,…,N-1}的离散傅里叶变换对为:
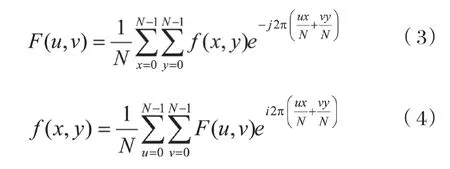
在大多数场合,假定图像为方阵,即M=N,此时离散傅里叶变换的变换对可简化为:
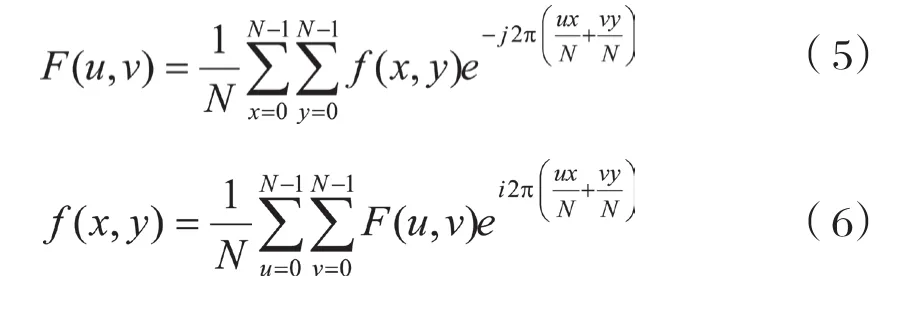
在离散傅里叶变换对中,F(u,v)称为离散信号f(x,y)的频谱,|F(u,v)|称为幅度谱,φ(u,v)为相位谱,它们之间的关系为:
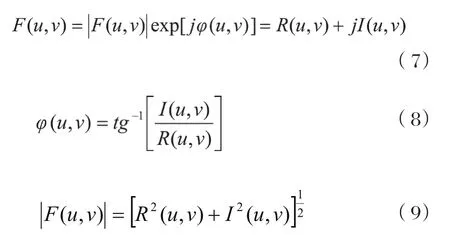
需要强调的是,离散变换一方面是连续变换的一种近似,而另一方面,其本身是严格的变换对。在以后进行的信号分析中,就可以简单地直接把数字域上得到的结果作为对连续场合的解释,两者之间得到了统一。
(2) 二维离散傅里叶变换的性质
在二维情况下,存在和一维变换相同的性质,如线性、位移、尺度、卷积、相关等。下面介绍在二维情况下才有的两条性质:
变换的可分离性由于离散傅里叶变换的指数项(变换核)可以分解为只含ux和vy的两个指数项的积,因此,二维离散傅里叶正反变换运算可以分别分解为两次一维离散傅里叶变换:
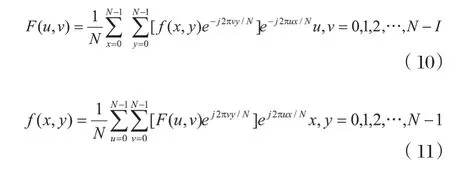
这一性质就是二维变换可分离性的含义。
若引入极坐标,使:

则f(x,y)和F(u,y)分别表示为f(r,θ)和F(w,∂),在极坐标中,存在以下变换对:
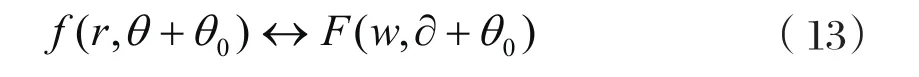
若将f(x,y)在空间域旋转角度θ0,则相应地F(u,y)在频域中也将旋转同一角度θ0。
2 滤波结果分析
无线激光通信中,图像噪声有很多,如高斯噪声、白噪声和椒盐噪声等。本文主要针对高斯噪声分析和比较了几种典型的空域滤波法的特点,试图通过在有噪声的图像上先进行低通滤波,然后高通滤波,找到一种恢复原始图像轮廓的去噪声方法。图像的很多噪声是高斯噪声,本文就主要以它们为例,试图在空域滤波法中,找到一种简单、有效的去除噪声方法。通过MATLAB实验和分析几种低通滤波和高通滤波的特点,得出了如下结论(结果见图2~图6):相对于邻域滤波法,对高斯噪声的处理效果更好。滤波的效果都与采用的模板、模板的大小有很大的关系。不管是邻域滤波法还是中值滤波法,由于都属于低通滤波,会使图像轮廓变得模糊,而高通滤波法中的基本高通滤波、高增益滤波、拉普拉斯算子滤波,以及拉普拉斯高斯算子,都可以使图像锐化,轮廓变清晰。因此可以考虑采用两者结合的方法对噪声进行处理,经过反复实验和分析,虽然没有得到去除高斯噪声的有效方法,但中值滤波结合拉普拉斯算子法或中值滤波结合拉普拉斯高斯算子法(需要作简单的灰度变换),都可以有效地消除椒盐噪声,且使图像轮廓基本上不变,其中中值滤波结合拉普拉斯算子法效果更好。

图2 带有高斯噪声的rice图像
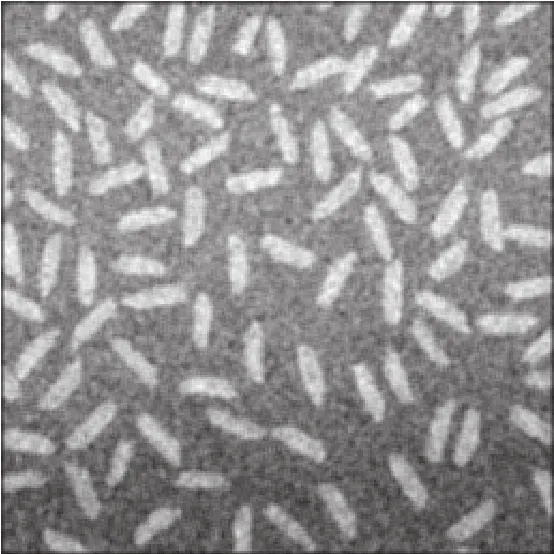
图3 经领域平均法滤波后的带有高斯噪声的图像
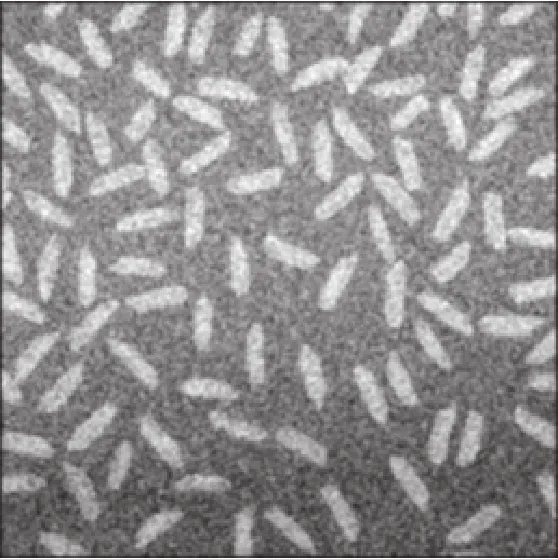
图4 经高斯模板处理后的带有高斯噪声的图像

图5 模板处理后的带有高斯噪声的图像

图6 经中值滤波后的带有高斯噪声的图像
3 结论
本文还对无线激光传输的图像信号噪声的处理进行了研究。在图像信号传输过程中必然会因为噪声的影响使得图像失真甚至变形。为了使含噪图像变得清晰,本文分析了几种含噪图像的去噪办法。图像去噪方法基本上可分为空间域法和变换域法两大类,前者是在原图像上直接进行数据运算,对像素的灰度值进行处理。它又分为两类:一类是对图像作逐点运算,称为点运算:另一类是在与处理像素点邻域有关的空间域上进行运算,称为局部运算。变换域法是在图像的变换域上进行处理,对变换后的系数进行相应的处理,然后进行反变换达到图像去噪的目的。
[1]杨齐民,王崇真,钟丽云,等.激光束与光纤耦合的研究[J].云南工业大学学报,1995,11(1):1-5.
[2]王俊峰,聂吉金.空间激光通信技术及发展[J].西安通信学院学报,2005(6):15-22.
[3]陈根祥,秦玉文,赵玉成,王勇译.光通信技术与应用[M].北京:电子工业出版社,1998:38-45.
[4]王俊生,田波,崔一平.大气激光通信技术[J].电子器件,2005:79-86.
[5]胡晟,艾勇.自由空间光通信中气象因素影响分析[J].光学与光电技术,2005:23-32.
[6]赵春晖,王伟.全方位多结构元形态滤波器[J].中国图像图形学报,1997,18(6):210-226.
[7]Akopian D,Vainio,Agaian,Astola.Processors for generalized stack filters[J].IEEE Trans,1995,43:1541-1546.
[8]刘极峰,原红玲.快速成型中激光烧结成型技术及应用[J].河南机电高等专科学校学报,2002,10(2):26-29.

