基于滑模矢量控制的异步电机调速系统★

李 琳， 雷 蓓

（西安石油大学 陕西省钻机控制技术重点实验室， 陕西西安 710065）

0 引言

异步电动机具有结构简单、牢固耐用、过流能力大、容易维护及价格低廉等优点，广泛应用在现代交流传动系统中。相对直流电机，它是一个高阶、非线性、强耦合的多变量系统，很难实现高动态性能。由于电力电子技术和交流电机控制理论的发展，许多现代控制方法应用到异步电机调速系统，如矢量控制、直接转矩控制、滑模

控制等，使异步电机调速系统性能越来越好[1-2]。

1 异步电机的矢量控制

矢量控制是通过坐标变换的方法，将异步电动机模型等效成直流电机模型，分解异步电机的定子电流，使能独立控制转矩和磁场有关的两个分量，实现对交流电动机转速和磁链控制的完全解耦。矢量控制系统框图如图1所示。

图1 矢量控制系统框图

1.1 矢量控制变频调速原理

根据矢量控制理论，遵循在不同坐标系下所产生的磁动势完全一致的原则，经过三相——两相变换和旋转变换，将异步电机定子电流空间矢量进行分解，在转子磁场定向坐标系(M-T)中将异步电机模型转换为直流电机模型来进行控制。在沿转子磁场定向的M、T 同步旋转坐标系中,对于笼型转子电机,转子短路,则um2=ut2=0，数学模型中的电压方程可简化成公式(1)所示。

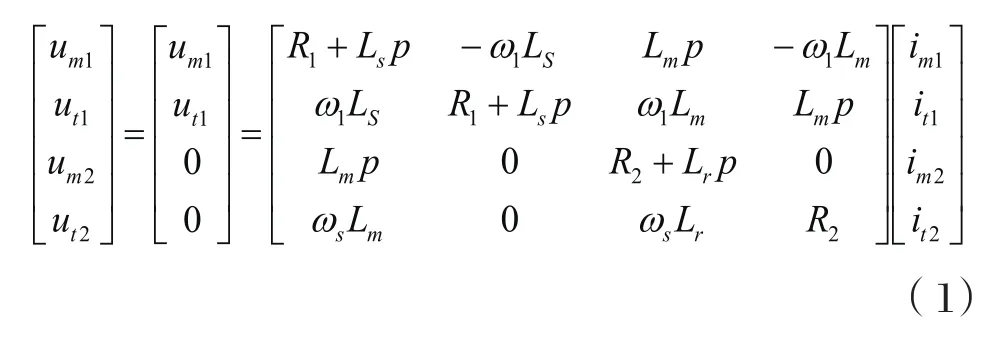
式中，um1,ut1为定子电压矢量的M分量和T分量；R1，R2为定子和转子电阻；Ls，Lr为定子和转子绕组的自感；Lm为定转子绕组间的互感；ω1为定子频率的同步角速度；ωs为转差角速度；p为极数。

在矢量控制系统中，被控制的是定子电流，因此必须从数学模型中找到定子电流的两个分量和其他物理量的关系。

电流的励磁分量为：

式中im1，it1为定子电流矢量的M分量和T分量；φ2为磁链；np为极对数。

总而言之，由于M、T坐标按转子磁场定向，在定子电流的两个分量之间实现了解耦（矩阵方程中出现零元素的效果），im1唯一决定磁链φ2，it1则只影响转矩，与直流电机中的励磁电流和电枢电流相对应，这样简化了多变量强耦合的交流变频调速系统的控制问题[3]。

1.2 异步电机矢量控制系统的仿真模型

在MATLAB/Simulink建立异步电机矢量控制变频调速系统的模型，它的仿真模型如图2所示。

图2 异步电机矢量控制变频调速系统仿真模型

异步电机矢量控制变频调速系统由转速控制器、坐标变换、异步电机与逆变器、电流滞环控制器、、磁链观测器和信号测量等子模块组成。

为了使异步电机调速系统具有更好的稳定性，响应速度快，超调量小，将滑模控制加入系统。在异步电机调速系统中，转速控制器采用的是PI控制，故针对它的转速控制器进行分析。

1.3 转速控制器模块

转速控制器的结构如图3所示，其中积分器采用离散时间积分器Saturation元件用于对输出转矩限幅。

图3 转速控制器

PI控制器为：

式中，KP为比例系数，KI为积分时间常数，ω*为给定的转速，ω为电机的输出转速。

由图2和图3可以看出，异步电机矢量控制变频调速系统中的转速控制器采用的是PI控制，PI控制结构简单，设计容易，但是随着系统性能的要求不断提高，传统的PI控制已经不能满足其要求。为了使异步电机矢量控制变频系统更加稳定，提出将滑模控制运用到转速控制器当中。

2 滑模控制器的设计

异步电机的参数(转子电阻、定子电阻等)和负载参数(转动惯量等)因地理环境变化而发生变化，异步电机的数学模型无法准确地反应调速系统的瞬态过程，使得一般的线性调节规律对交流调速系统有着一定的局限性[4]。滑模变结构控制是一种特殊的非线性控制，其非线性表现为控制的不连续性。它具有响应速度快，超调量小，控制精度高，较强的鲁棒性与抗干扰等优点，并能适应有特殊控制要求的场合[5-6]。

滑模控制器结构如图4所示，它的关键在于开关面函数的选取。

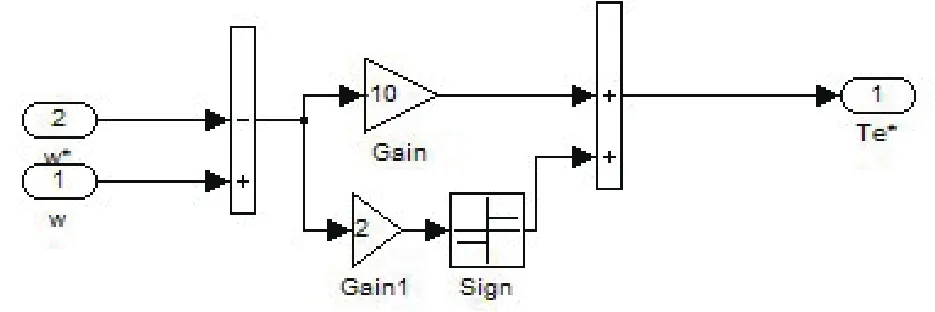
图4 滑模控制其结构图

定义开关面函数为：

速度环PI调节器采用滑模控制器，则滑模控制器设计为：

式中，Tes为转矩的输出，λ1、k为正常数。

3 仿真实验

采用图2 所示的仿真模型，对异步电动机矢量控制系统进行仿真。异步电动机的参数如下：额定功率3.7 kW；线电压380 V；额定频率60 Hz；定子内阻0.087 8 Ω；定子漏感0.8 mH；转子内阻0.228 Ω ；转子漏感0.8 mH；定转子漏感34.7 mH；极对数为2；电流调节器采用滞环型的PWM 控制器，滞环宽度为20 A[7]。速度环PI控制下加负载的电机转速图形如图6所示。转速的给定值为120 r/s，PI控制器的参数KP=2，KI=20；滑模控制器的参数λ1=2，k=10。

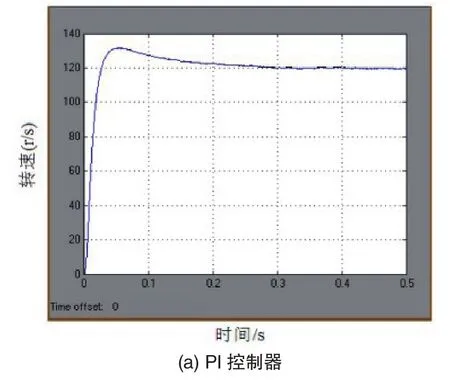
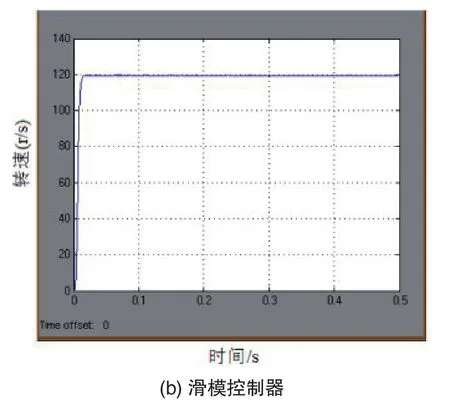
图5 异步电机转速的仿真图形

由图5可以看出，传统的PI控制速度响应曲线超调较大，采用滑模控制速度响应曲线超调很小，响应速度很快，短时间内使系统达到稳定。

若在0.1 s的时候给电机突然加入负载，异步电动机的转速负载如图6所示。

图6 突加负载下异步电机的转速

由图6可以看出，给电机在0.3 s时突加负载，电机的输出转速突降到80 r/s，经过0.4 s之后，又恢复到120r/s,因而系统具有良好的抗负载扰动能力。

4 结论

针对异步电机运行过程中难以实现高动态性能的问题，建立了异步电机矢量控制变频调速系统模型，运用了滑模矢量控制策略。该控制策略具有很好的控制特性，可以增强系统的抗干扰性，减少超调量，提高系统的响应速度。

[1]吕华林.异步电机矢量控制变频调速系统的研究[D].武汉:武汉理工大学,2010.

[2]白晶晶.基于simulink的交流电机矢量控制调速系统的仿真[J].鸡西大学学报,2008,8(3):86-89.

[3]陈伯时.电力拖动自动控制系统[M].北京:机械工业出版社,2000.

[4]胡俊达.基于遗传算法的模糊自适应控制在DTC的应用[J].电工技术学报,2004,19(6):78-84.

[5]刘金琨.滑模变结构控制MATLAB仿真[M].北京:清华大学出版社,2005.

[6]胡俊,达胡慧.基于滑模变结构控制的异步电机速度控制的应用研究[J].大电机技术,2006(5):32-35.

[7]邵杰.基于Matlab/Simulink 异步电机矢量控制系统仿真[J].电气传动,2009,28(3):73-76.