Polar码在OFDM系统中应用研究
郑芝芳,杨 华
(南京邮电大学,南京 210003)
0 引言
OFDM[1](Orthogonal Frequency Division Multiplexing)即正交频分复用技术,实际上OFDM是MCM(Multi-CarrierModulation),多载波调制的一种。其主要思想是:将信道分成若干正交子信道,将高速数据信号转换成并行的低速子数据流,调制到每个子信道上进行传输。OFDM技术具有频谱利用率高、抵抗多径衰落能力强、消除码间干扰能力强、接收机结构简单、成本较低等优点,非常适合应用于无线高速数据传输, 已被列入4G无线通信系统的解决方案中, 同时OFDM 技术也将成为未来高速宽带无线通信的主导力量[2]。在OFDM系统中插入保护间隔后可以避免符号间干扰并减少信道间干扰问题,同时信号经过多径衰落信道到达接收端的所有子载波上的信号幅度可能不同。事实上,某些子信道由于深衰落可能会完全被淹没,必将引起误码率的急剧增大,信息质量急剧下降。编码可以纠正或检测在衰落信道中的随机错误。为此, OFDM技术必须与纠错码技术相结合才能真正发挥作用。OFDM 系统在子载波间进行编码,形成 COFDM(code Orthogonal Frequency Division Multiplexing) 方式。
Polar码是Erdal Arikan于2007年提出的一种基于信道极化理论定义的线性分组码[4]。作为一种线性分组码,Polar码与LDPC码很相似,但相比LDPC码,它在理论上能够达到香农限,并且有着较低复杂度的编译码算法,仅为O(NlogN),其中N为码长。自提出以来,Polar码引起了人们极大的关注,其理论也得到了不断的完善。已被推广于信源编码、信源信道联合编码、窃听信道编码等。将Polar码应用于OFDM 系统中,不但可以简化OFDM 系统模型, 而且可以较大地改善OFDM 系统误码率。
本文研究Polar码在OFDM系统中的应用。在给出Polar码基本理论的基础上,讨论了Polar码的译码迭代次数和码率对OFDM系统性能的影响。同时在码率和码长一定的情况下,在高斯信道下仿真系统性能,以便说明Polar码在图像的优越性。
1 基于Polar码的OFDM系统性能研究
1.1 COFDM系统
OFDM技术实际上是把信道分割成中心频率各不相同的许多个子信道,把宽带通信化为多个并行的窄带通信。通信中由于多径效应会使接收信号某些频率分量增强,某些频率分量减弱。利用编码技术可以使部分频率分量减弱部分的数据得以恢复。这就说明OFDM 通信系统也需要利用信道编码技术,系统中各子信道需要通过编码使其相互联系,来解决通信过程中不可避免的突发干扰。Polar码是在理论上能够达到香农限,并且有着较低复杂度的编译码算法。结合Polar码与OFDM系统给出Polar-COFDM系统的简化模型框图(见图1),在发送端,输入的数据流经Polar码编码后,进行基带调制(QAM,M-PSK 调制),然后送入OFDM调制器,OFDM调制过程中插入循环前缀和导频,最后进入信道;而在接收端,是发送端的逆过程,先根据导频进行信道估计,去循环前缀,再经基带解调器、Polar码译码输出译码比特流。系统通过Polar 码对OFDM 各个子载波实现了联合编码,具有较强的抗衰落能力,使系统的性能得到提高。
在本文中主要对高斯信道进行仿真。
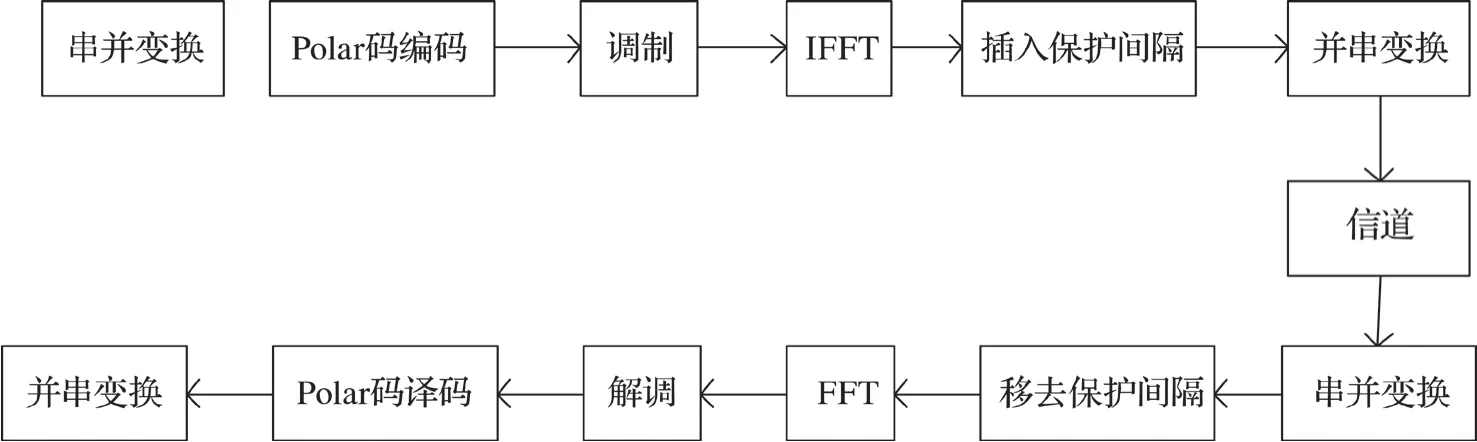
图1 COFDM系统框图
1.2 Polar码对COFDM系统性能的影响
作为一种线性码,Polar码最重要的是生成矩阵GN(A)的选择。下面以G(16,4)为例说明生成矩阵的选择过程。
其过程描述如下:先得到N阶生成矩阵。
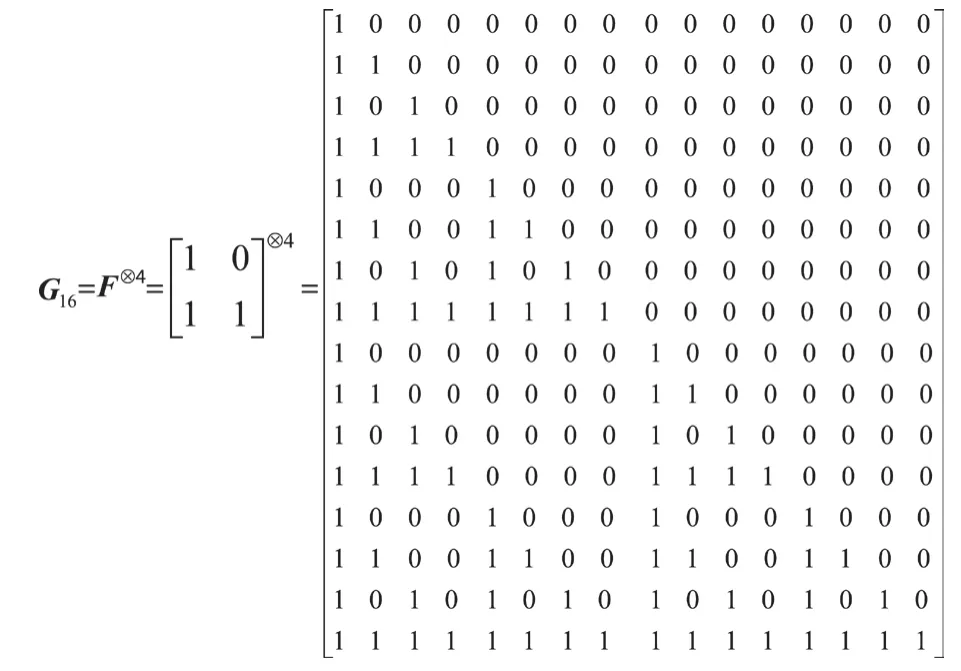
取初值Z(W16(0))=0.5,根据递推公式计算得到Z(W16(i)),分别是 :Z(W16(i))=[1,0.899,0.963,0.227,0.985,0.362,0.532,0.007,0.992, 0.467,0.653,0.014, 0.772, 0.037, 0.100,0](i=1,2,…,16)。然后, 对Z(W16(i))进行降序排列,选择Z(W16(i))(i=1,2,…,16)中较小的4个比特信道,即排序后最小4个值的行号,形成集合A,即,A=[14,12,8,16]。在矩阵G16中以A集对应的行构成生成矩阵G16(A)。它的码率r=4/16=0.25。

下面就Polar码对OFDM系统性能影响进行数值仿真,包括Polar码译码迭代次数与码率对OFDM系统性能的影响。
(1) Polar码译码迭代次数对COFDM系统性能的影响
同其他信道编码一样,Polar码译码的迭代次数对Polar码的性能具有一定的影响。我们发现当迭代次数增加时,译码正确率相对提高,但是迭代次数增加同时也影响到计算的复杂度,而且迭代次数增加到一定程度对误码率的改善不会很明显。
图2所示的是Polar-COFDM系统在高斯信道下的性能仿真曲线图。仿真时码长为2048,码率为0.25,随着迭代次数的增加,系统的BER性能提高。从图中可以看出,在高斯信道中Polar-COFDM在迭代次数约为120时收敛,这里即使再增加迭代译码的次数译码性能将不会有明显的提高。所以接下来做仿真选择的迭代次数为120次。
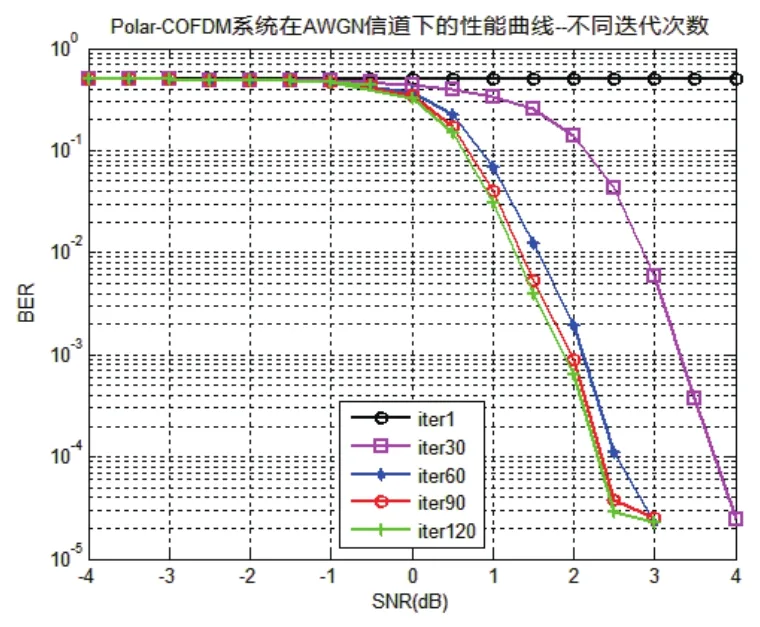
图2 Polar-COFDM在高斯信道下的仿真曲线
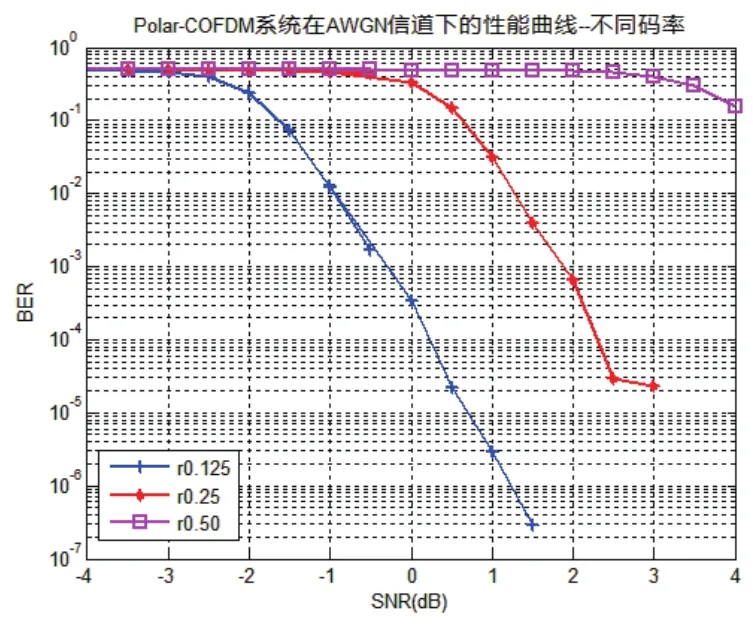
图3 码率减小时的仿真曲线
(2) Polar码码率对COFDM系统性能的影响
线性码编码过程中的重点就是生成矩阵获取。Polar码作为一种线性码,其生成矩阵的选择在很大程度上依赖巴氏参数Z(WN(i))。我们可以根据Z(WN(i))的值,选择生成矩阵GN中较小的K行的行号作为信息位集合A,得到生成矩阵GN(A)。当码长N一定、码率r减小的时候,K=N×r随之减小。这样我们在选择巴氏参数Z(WN(i))的时候就可选到更小的Z(WN(i))值。这就相当于在信道极化中,能够选择到更接近于无噪信道进行数据传输。图3是Polar码不同码率对COFDM系统的影响,其中信息们长均为512。图3说明随着码率减小,Polar码在OFDM系统中的传输性能会越来越好。
2 结论
信道编码是图像传输不可或缺的一部分,Polar码是至今为止在理论上能够达到香农限的一种编码方法,它的应用研究报道较少。本文研究Polar码在OFDM系统中的性能,分析Polar码的译码迭代次数和码率对系统性能的影响。说明在一定条件下译码迭代次数增加,和码率减小,都能使Polar-OFDM系统的性能更好,符合理论过程。
[1]汪裕民.OFDM关键技术与应用[M].北京:机械工业出版社,2006:13-28.
[2]周凯,张建华.基于低密度校验码的OFDM 系统及其误码性能的研究[M].黑龙江工程学院学报:自然科学版, 2007,21(2).
[3]刘元安.宽带无线接入和无线局域网[M].北京:北京邮电大学出版社,2000.
[4]E.Arlkan.Channel polarization: A method for constructing capacity-achieving codes for symmetry binary-input memoryless channels[J].IEEE Transactions on Information Theory,2009,55:3051-3073.
[5]E. Arlkan.Channel combining and splitting for cut off rate improvement[J].IEEE Transactions on Information Theory,2006, IT-52:628-639.
[6]E.Arlkan,E.Telatar.On the rate of channel polarization[J].IEEE International Symposium on Information Theory, 2009:1493-1495.
[7]S.B.Korada.E.Sasoglu.R.Urbanke.Polar codes:characterization of exponent, bounds, and constructions[J].IEEE International Symposium on Information Theory,2009:1483-1487.
[8]H.Mahdavifar,A.Vardy.Achieving the secrecy capacity of wiretap channels using Polar codes[J].IEEE International Symposium on Information Theory Proceedings,2010: 913-917.

