适用于高阶QAM解调的载波恢复算法及其实现验证
吕昌波,霍文辉,王进刚
(重庆邮电大学 光电工程学院 检测电路与信息传输系统研究中心)
0 引言
全数字QAM解调系统中,频偏和相偏是影响系统解调性能的最主要因素[1],其在星座图上表现为使星座点产生旋转,旋转到其相邻星座点的区域,从而导致判决出错,使系统性能急剧恶化。另外,随着QAM信号阶数的提高,其对同步性能的要求也越高。因此,必须在接收端对系统中的频偏和相偏进行更精确的补偿,使得接收端与发送端的载波信号达到同频同相,来提高解调系统的性能。对于高阶QAM 系统,传统的延迟相干、全波整流、科斯塔斯环、乘方环路并非理想的载波同步方案[2]。1980年,L.E.Franks对数字信号的载波相位估计作了详细的探讨,并提出了一种基于最大似然参数估计(ML)的误差估计算法[3]。这是理论上的最佳算法[4-5],但是求似然函数的过程比较复杂,实现起来非常困难。之后出现的面向判决DD(Decision Directed)算法[6-7]是利用判决后的数据与判决前的数据进行比较来得到相位差,这种算法实现相对简单,因此其得到了广泛的应用。本文对判决反馈实现方法和常见的两种DD算法进行了简单的介绍,并结合16QAM解调系统给出其MATLAB/Simulink实现并对其进行分析。
1 判决反馈环算法
传统的面向判决锁相环法(Decision Directed PLL,即DD-PLL,亦称判决反馈环)的实现框图如图1所示,假定输入的信号y(n)已经过了自动增益控制、定时恢复和均衡,首先y(n)与数控振荡器的输出相乘,产生相干解调信号S(n),然后利用(n)和S(n)计算得到DD-PLL的鉴相输出,其中(n)为S(n)的逐电平判决输出。
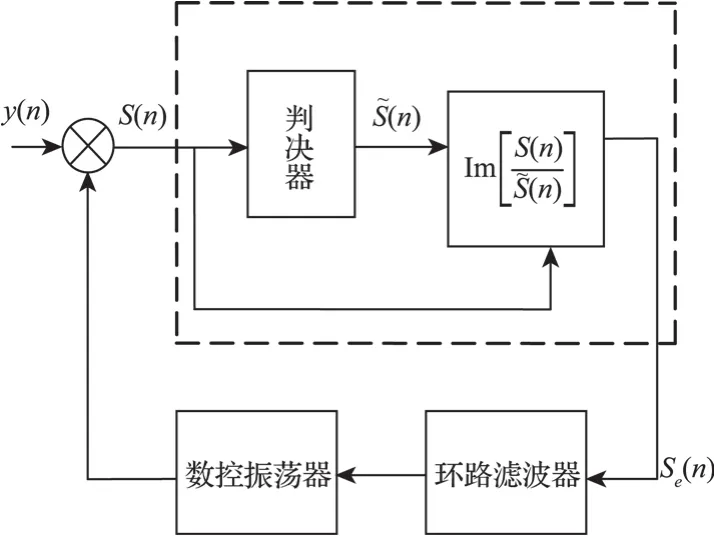
图1 DD-PLL的结构框图
DD-PLL的鉴相输出为:
式中S(n)、(n)分别是载波恢复环路输入信号y(n)的软判决和硬判决的值,(n)是S(n)经过判决器输出的信号,Se(n)是鉴相器输出的相位误差信号,表示取虚部运算。鉴相器输出Se(n)经过环路滤波器后用于驱动数控振荡器工作,数控振荡器输出的频率就是我们需要的与信号同步的工作频率。

常用的DD算法有两种[8]。
1.1 算法1
该算法相位检测器输出的相位误差为

其中, sgn表示取符号位操作。该算法可以用16QAM信号的星座图来说明。以图2上A点为例,当信号落在A点上时,相位误差为零,即接收的信号不存在相位误差;当接收的QAM信号点存在小的相位误差θ时,A点会围绕坐标原点旋转,落在标有“+”或“-”的区域中,据此可以计算出相应的相位误差。
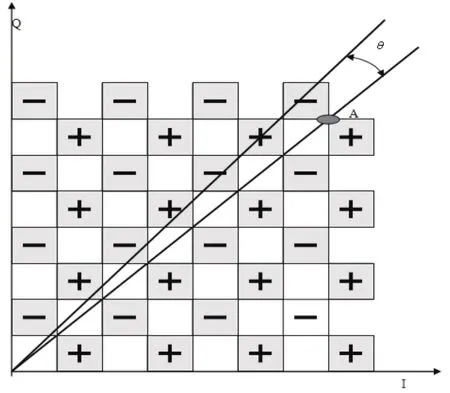
图2 QAM星座图
1.2 算法2
该算法相位检测器输出的误差值为:
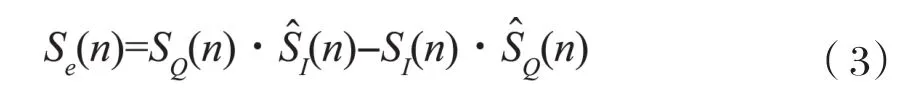
在接收信号信噪比较低时,判决器的输出(n)不可信,但是(n)的符号位还是比较可信的,又因为sgn [(n) ]= sgn[S(n)],因此可以用sgn[(n)]来替代(n),所以上式可变为:
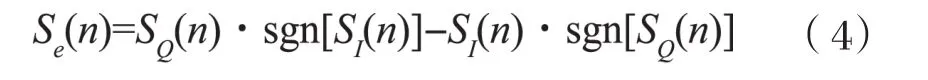
2 Simulink仿真与性能分析
为了对DD算法进行验证,本文给出了算法二的 Simulink基带仿真模型,如图3所示。

图3 16QAM Simulink仿真模型
DD-PLL由鉴相器、环路滤波器和NCO 3个部分组成。解调器的输入信号与NCO输出的正余弦信号所合并的复数信号相乘后,经过DD鉴相器得到相位误差信号经过环路滤波器滤除高频分量后,去修正数控振荡器的频率控制字, 完成闭环控制。具体仿真参数如下:
1) 码元速率 2 MHz/s
2) 采样速率 8 MHz/s
3) 信噪比(SNR)30 dB
4) 初始相偏 30°
5) 初始频偏 3 kHz
对不同相偏和频偏的仿真星座图如图 4所示。

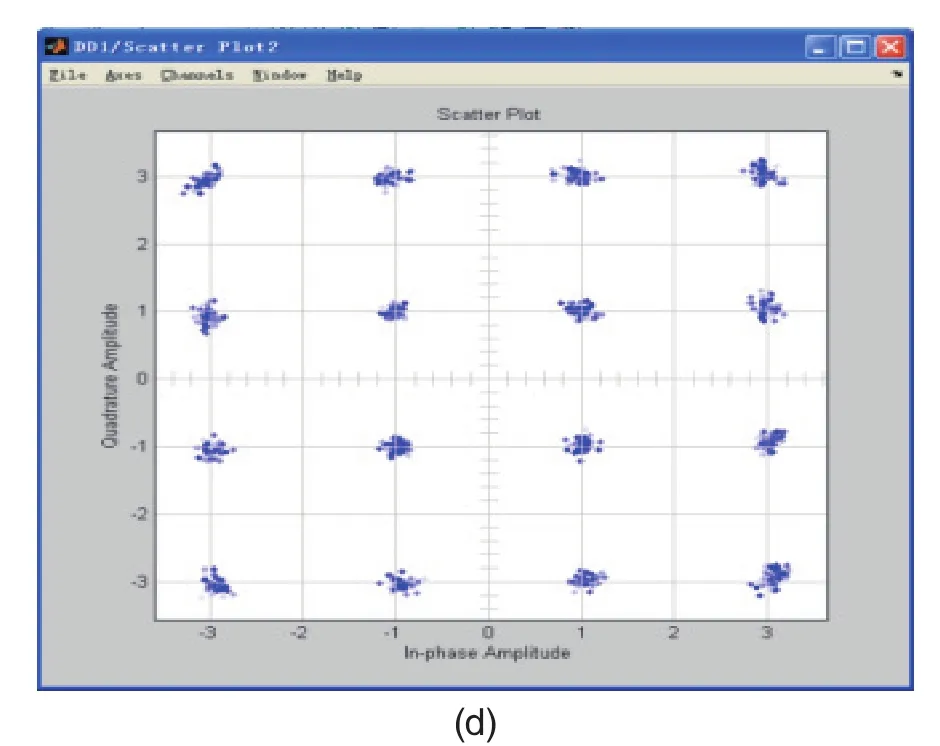
图4 16QAM Simulink仿真星座图
图4 中,(a)为接收机的输入信号在初始相偏为30°时的星座图;(b)为接收机输入信号在初始相偏为30°、初始频偏为3 kHz时的星座图;(c)为初始相偏为30°初始频偏为3 kHz时载波恢复中信号的星座图;(d)为初始相偏为30°初始频偏为3 kHz时,经过DD-PLL载波恢复后信号的星座图。由上图可以看出,在存在30°相偏、3 kHz频偏时,经过一定的归一化单位时间星座图趋于收敛,再经过一定的单位时间后DD环路已经完全补偿掉输入信号中存在的频偏相偏。
通过调节环路滤波器的直通路系数和积分路系数,可以改变环路的环路带宽和环路增益等参数,进而影响收敛时间、捕获带宽和稳态抖动等性能。通常环路带宽越大,环路收敛越快,但误差值稳态抖动越大;环路增益越大,环路收敛越快,稳态抖动越大[9]。图5为经过环路滤波器之后的相位误差跟踪情况,可以看出接近700个点时相位误差基本趋于0,在900个点之后DD-PLL环路已经完全跟踪上信号的相位,与星座图所示情况一致。

图5 16QAM Simulink仿真相位跟踪情况
3 结论
DD算法利用全部星座点经过判决后的数据与判决前的数据比较得到相位误差,这种算法简单有效,广泛应用于高阶QAM解调系统中。本文给出了DD算法的Simulink实现方法,并对其进行了验证分析。因为DD算法是对数据进行直接判决的,所以要求初始的相位偏差必须足够的小。如果存在较大的初始相位误差则很容易出现参数估计的错误;在信噪比较低的时候,估计性能也将随着信号判决的误码率的提高而迅速下降。这些都限制了它的使用范围,所以实际应用中DD算法可以用于载波频偏捕获之后对载波相位进行跟踪,这样可以获得较小的稳态相位误差[10]。
[1]邓青.数字QAM基带解调技术研究与实现[DB/OL]. http://www.mscbsc.com/bbs/viewthread.php?tid=302328 ,2007.
[2]李和.一种QAM载波相位盲识别算法的研究与实现[J].电测与仪表,2009,46(525):44-46.
[3]Hua Wang,Chaoxing Yan,Nan Wu.Maximum Likelihood Clockless Feedback Phase Recovery for MPSK Signals[C].Vehi cular Technology Conference Fall (VTC 2010-Fall),2010 IEEE 72nd,2010:1-5.
[4]John G.Proakis.数字通信[M].4版.张力军 译.北京:电子工业出版社,2005.
[5]Coastas.N.Georghiades.Blind carrier phase acquisition for QAM constellations[J].IEEE Trans Commun,1997,1(45).
[6]Shay Landis,Ben-Zion Bobrovsky.Decision Directed versus Non-Data Aided PLLs:A Comparative Review[J]. IEEE TRANSACTIONS ON COMMU NICATIONS,2010,58(4):1256-1261.
[7]Gappmair.W, Holzleitner.J.Detector characteri-stic for decision directed carrier phase recovery of 16/32-APSK signals[J].Electronics Letters,2006:1464-1466.
[8]Ki·Yun Kim and Hyung·Jin Choi.Design of Carrier Recovery Algorithm for High Order QAM with Large Frequence Acquisition Range[C].IEEE International Conference on Communications,2001,4:1016-1020.
[9]张厥盛,郑继禹,万心平.锁相技术[M].西安:西安电子科技大学出版社,1998.
[10]许华,郭建新,郑辉.高阶QAM信号多级盲相位估计方法及其性能仿真[J].系统仿真学报,2004,16(7).

