卫星阵馈反射面赋形波束天线的内积波束赋形方法

张亦希 张恒伟

（1.西安交通大学微波工程与光通信研究所，陕西 西安710049；2.63880部队，河南 洛阳471003）

引 言

为了提高轨道资源、频率资源的利用率，近年来卫星天线已广泛地采用了赋形波束天线技术。卫星赋形波束天线与传统的天线技术不同，它可以只在指定的、任意形状的服务区域（如：在中国境内）内具有较高的增益，而在此区域以外则增益很低，因此它就具有许多传统天线技术所没有的优点：1）可以有效减小来自邻近卫星通信系统的干扰，从而提高卫星轨道资源的利用率；2）可以提高天线的增益，从而提高卫星功率的利用率；3）可以在不同的波束间对频率进行复用，从而提高频率资源的利用率［1－4］。

图1 卫星阵馈反射面天线的组成

阵馈反射面天线因为具有体积小、重量轻，且能对方向图进行重新配置和对干扰进行自适应抑制等优点，而成为一种较为常见的卫星赋形波束天线形式。它主要由一个反射面天线、一个馈元阵以及一个波束成形网络组成，如图1所示。反射面天线一般是抛物面天线或卡塞格伦天线，而馈元阵则通常由喇叭天线组成。馈元阵放在反射面天线的焦平面上，产生的波经过反射面的反射会在远场区形成一组形状近似相同、均匀分布的点波束阵，波束成形网络则通过调整各个馈元的激励系数，来对这些点波束进行加权、叠加，从而形成一个只覆盖指定服务区域的赋形波束。同时阵馈反射面天线由于可以在工作过程中对各馈元的激励系数进行修改，所以可以对其方向图进行重新配置，对干扰进行自适应抑制。

波束赋形方法主要用来寻找一组馈元的最佳激励系数，以使天线的方向图成为人们需要的任意形状。目前，虽然已有不少有效的赋形方法，如最小p乘法［5］、最小最大法［6］、线性约束最小方差（LCMV）方法［7］等。但这些传统的赋形方法在实际应用中存在一些缺点。例如：最小p乘法和最小最大法是迭代算法，运算效率很低。另外，这两种算法和LCMV方法一样，都是使赋形波束在某些方向上逼近目标方向图的采样值，而这些采样的数量由于受到天线自由度的限制一般都小于采样定理所要求的数量，所能得到的赋形波束对目标方向图采样的选择十分敏感。为获得满意的赋形波束，这些传统赋形方法往往需要对目标方向图采样的数量和位置进行反复调整，实际应用起来比较困难。因此，本文提出了一种基于内积运算的波束赋形方法。该方法是把目标方向图作为一个整体，使赋形波束与目标方向图在几乎所有方向上的误差总和最小，实际使用起来十分方便。同时它也是一种解析算法，具有较高的赋形精度和运算效率。

1 理论分析

1.1 卫星阵馈反射面赋形波束天线的数学模型

假设卫星阵馈反射面赋形波束天线的馈元阵共有N个馈元，且当第n个馈元的激励系数为1，其他馈元的激励系数全部为零时，天线产生的远区场为fn（x1，x2），则当 N 个馈元的激励系数分别为wn（n＝1，2，…，N）时，天线所产生的合成场f（x1，x2）为

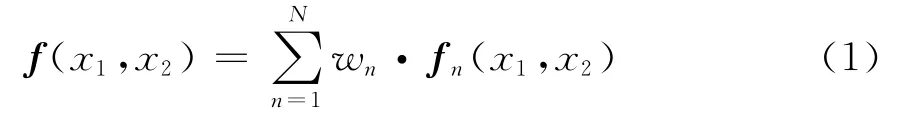
式中x1，x2分别为观察点的方位角和俯仰角［8－9］。fn（x1，x2）在天线几何结构已知的条件下，可用物理光学法来确定［10－11］。

对阵馈反射面天线进行波束赋形，是要在目标方向图已知的情况下，求一组最佳激励系数以使赋形波束与目标方向图间的误差最小。阵馈反射面天线的波束赋形问题可以用数学方法表示为

式中：fd（x1，x2）为天线的期望场；｜·｜表示矢量的模值；‖·‖表示函数的范数。赋形误差E的定义方法及最小值求法的不同，就形成了不同的波束赋形方法。

1.2 传统的波束赋形方法

目前较为常用的波束赋形方法主要有最小p乘法、最小最大法和LCMV方法等。

对于最小p乘法，其赋形误差定义为

以天线在K个采样点处合成场与期望场间误差的总和为优化目标函数，用现有的优化算法，如Fletcher－Powell算法，不断地调整各馈元的激励系数直到目标函数值达到最小。

对于最小最大法，其赋形误差定义为

最小最大法通常用在要求赋形波束的最大旁瓣电平或者服务区域内天线增益的最大起伏要小于某个值的场合。

对LCMV方法，其基本思想则是在保证天线在Km个方向（x1i，x2i）（i＝1，2，…，Km）上的合成场等于期望场的条件下，使天线的总辐射功率最小，即

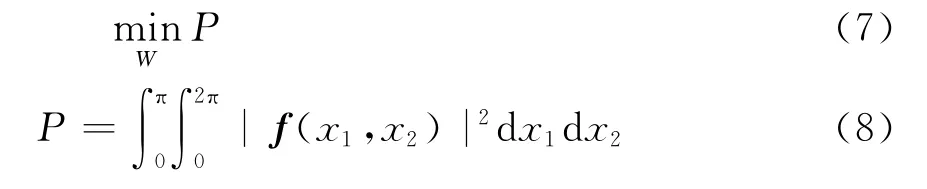
约束条件

1.3 基于内积运算的波束赋形方法

由于，式（3）可以看成是误差e（x1，x2）的范数，因此式（2）就可以看成是要在由N 个函数fn（x1，x2）所张成的线性空间中求fd（x1，x2）的最佳逼近。故e（x1，x2）必与这个线性空间fn（x1，x2）正交。于是，对任意整数m（1≤m≤N），对式（4）两边同时与fm（x1，x2）作内积运算，则有

式中＜·＞表示两个函数间的内积运算。若赋形误差E定义为

则式（10）的左边为

式中＊表示复共轭。由于式（12）实际上仅是一个与m有关的常数，故可记作dm.同理式（10）的右边也是一个仅与m和n都有关的常数，可记作cnm.于是，式（10）可重写为

式（13）可写为矩阵形式

式中：D＝［d1，d2，…，dN］T；W＝［w1，w2，…，wN］T；

因此，天线的最佳激励系数就是方程（14）的解

由于每个点波束中心的位置各不相同，且间隔较大，各个点波束的远区场是近似正交的，矩阵C满秩，方程（14）有唯一解。

2 仿真结果分析

以下对一个以中国本土为服务区域的卫星阵馈反射面赋形波束天线，分别用最小p乘法、最小最大法、LCMV方法和内积波束赋形方法进行赋形，以验证这种基于内积运算的波束赋形方法的有效性和优越性。天线的馈元阵选为馈元数为61的正六边形阵。为了便于计算，fn（x1，x2）用D.Sonderogger等人所给的近似表示式来代替［12］，具体如下

式中：J1（u）是变量为u的第一类一阶Bessel函数；da为天线有效口径的直径（单位：m）；η为天线的效率；f为工作频率（单位：Hz）；c为光速（单位：m／s）；x1n和x2n分别为第n个波束中心的方位角和俯仰角（单位：（°））。在本例中，波束间隔选为0.85°，η＝0.25，f＝6GHz，da＝4.04m，此时点波束的宽度为0.85°.

图2 最小p乘法得到的赋形波束方向图

在相同情况下对中国本土用不同的赋形方法赋形后，所得到的赋形波束分别如图2、4、6、8所示，各图中的黑色粗线为中国本土的边界线在卫星视场内的投影，六根黑色细线分别为天线的实际方向图在－3dB、－5dB、－10dB、－15dB、－20dB和－30dB－30dB时的等高线。各赋形波束所对应的目标方向图采样如图3、5、7、9所示，各图中o表示目标方向图在主瓣区域内的采样，而＊则表示旁瓣区域内的采样。比较图3、5、7、9可见：最小p乘法、最小最大法、LCMV方法由于都是优化算法，故受到天线自由度的限制，只能采用数量较少、且位置不规则的采样，为获得满意的赋形波束，天线设计人员往往需要对目标方向图采样的数量和位置进行反复调整，实际应用起来十分困难。而内积方法由于可以选择数量较多、位置规则的采样，如图9所示分布在正四边形网格上的采样，在这些采样点上计算dm和cmn，由式（14）计算出最佳激励系数，只要采样点的密度满足采样定理的要求，即采样点的密度应大于目标方向图频域带宽的2倍，最佳激励系数就可以使赋形波束与目标方向图在几乎所有方向上的误差总和最小，所以，内积方法不用反复调整采样点的数量和位置，就可以产生满意的赋形结果。在本仿真中，三种传统赋形方法在得到图2、4、6中的赋形波束前，都对约束条件进行几十次甚至上百次的调整，而内积方法则只运行了一次就得到了图8中的赋形波束。

图3 最小p乘法的采样点位置

同时，比较图2、4、6、8可见，LCMV方法和内积方法的赋形精度最高，远高于最小p乘法和最小最大法。同时这四种方法在同一台计算机上的运行时间分别为：最小p乘法1.9min，最小最大法7.24min，LCMV方法为0.004 95min，内积方法则为0.29min.因此，由于这种赋形方法和LCMV方法都是解析算法，故它们的运算效率也远高于前两种方法。

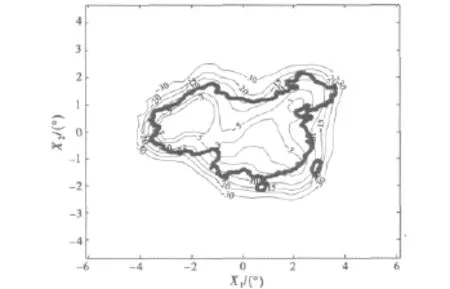
图4 最小最大法得到的赋形波束方向图

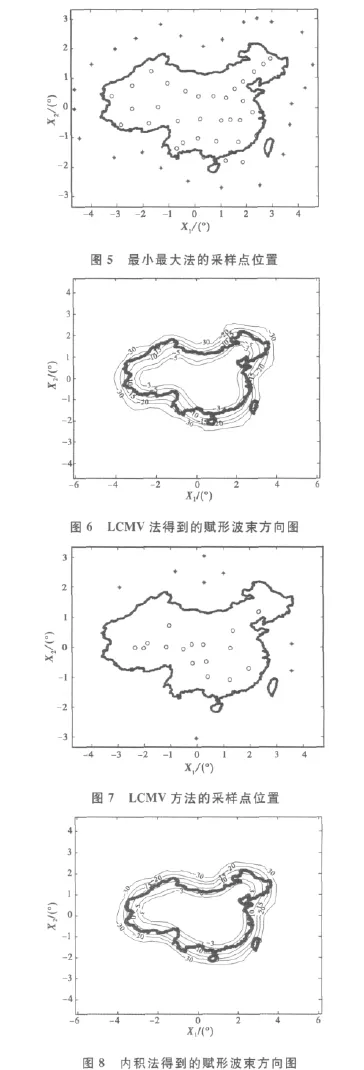
图9 内积法的采样点位置

3 结 论

由以上分析可见：由于内积赋形方法首先是一种解析法，因此它有较高的赋形精度和较快的运算速度，同时它是把目标方向图作为一个整体，是使赋形波束与目标方向图在几乎所有方向上误差的总和最小，而不是在一些有限数量的采样点上的误差总和最小，所以不需要对选择采样点的数量和位置进行反复调整，实际使用起来十分方便。

［1］PRATT T，BOSTIAN C W，ALLNUTT J.Satellite Communications［M］.2nd Edition.New York：John Wiley ＆Sons，2003.

［2］ROEDERER A G，JENSEN N E，CRONE G A E.Some European satellite－antenna developments［J］.IEEE Antennas and Propagation Magazine，1996，38（2）：9－21.

［3］HWANG Y.Satellite antennas［J］.Proceedings of IEEE，1992，80（1）：183－193.

［4］ZAGHLOUL A I，HWANG Y，SORBELLO R M，et al.Advances in multibeam communications satellite antennas［J］.Proceedings of IEEE，1990，78（7）：1214－1232.

［5］PATEL P D，CHAN K K.Optimization of contoured beams for satellite antennas［J］.IEE Proc Microwave，Optics and Antenna，1985，132（6）：400－406.

［6］SCHJAER－JACOBSEN H，MADSEN K.Synthesis of nonuniformly spaced arrays using ageneral nonlinear minimax optimization method［J］.IEEE Trans on AP，1976，24（4）：501－506.

［7］张亦希，傅君眉，汪文秉.LCMV方法在卫星多波束天线赋形中的应用［J］.电子学报，2002，30（3）：332－334.ZHANG Yixi，FU Junmei，WANG Wenbing.Application of LCMV algorithm to pattern synthesis for satellite multiple－beam antenna［J］.Acta Electronica Sinica，2002，30（3）：332－334.（in Chinese）

［8］张亦希，傅君眉，汪文秉.卫星多波束天线不规则馈元阵形赋形的研究［J］.电子学报，2002，30（6）：777－779.ZHANG Yixi，FU Junmei，WANG Wenbing.Research on pattern synthesis for irregular feed array configuration in satellite multiple－beam antennas［J］.Acta Electronica Sinica，2002，30（6）：777－779.（in Chinese）

［9］ZHANG Yixi，FU Junmei，WANG Wenbing.Frequency－domain principle of pattern multiplication for array－fed reflector antennas［J］.IEEE Microwave and Wireless Components Letters，2004，14（7）：328－330.

［10］IMBRIALE W A，INGERSON P G，WONG W C.Large lateral feed displacements in a paraboloc reflector［J］.IEEE Trans Antenna and Propagation，1974，22（6）：742－745.

［11］RUZE J.Lateral－feed displacement in a paraboloid［J］.IEEE Trans Antenna and Propagation，1965，13（9）：660－665.

［12］SONDEROGGER D.Satellite Antenna Pattern Optimization and Loading Model：Methodology Report［R］.Defense Information System Agency，1992.