频率选择表面电磁特性的多元自适应采样分析

马 鑫 万国宾 王 威 万 伟

（西北工业大学电子信息学院，陕西 西安710129）

引 言

频率选择表面（FSS）结构由沿二维方向上周期排列的单层或多层级联导体单元组成，具有较强的空间滤波特性，在雷达天线罩、副反射面等方面有着广泛应用。因此，近年来国内外学者对FSS的分析理论和工程应用方面进行了深入研究［1］。文献中有多种FSS电磁特性的分析方法，其中谱域矩量法（MoM）因其较好的通用性和精度而被普遍采用［2］。但是当FSS单元形状复杂或电尺寸较大时，直接矩量法求解大型矩阵方程非常耗时，需要寻求高速的算法。从加速算法本身着手，可采用共轭梯度法［3］，快速多极子［4］等方法，但是这些方法仅对单个点的计算非常有效。在FSS的分析与设计中，常常需要在较宽的频带或是入射角范围内获得散射特性［5］，如果逐点重复求解矩阵方程，必将导致巨大的计算工作量。因此，研究一种逼近方法快速分析FSS散射特性具有重要的现实意义。

目前，参数模型逼近的求解方法已被广泛用于电磁散射的计算中。其中，渐近波形估计法通过采样点的导数信息构建多项式模型，快速分析FSS的宽带电磁散射特性［6］。但计算的准确性受到了级数收敛半径的限制，并占用了大量的内存空间。Maehly逼近法依据Chebyshev节点变换关系选择采样点，基于Chebyshev级数展开的有理函数模型拟合未知电流［7－8］。由于参数模型的系数通过线性方程组求解，当采样点数较多时，可能导致病态矩阵的产生，影响数值计算的稳定性。自适应频率采样（AFS）法基于Neville迭代算法在宽频范围内建立任意阶数的有理多项式，用于分析微波电路的散射特性［9］和FSS的电磁特性［10］，大大缩减了整个频率响应的计算时间。但AFS法局限于对频率参数的自适应采样，在FSS分析中还需要考察入射方向、结构参数等对FSS电磁特性的影响。

本文旨在将一维的AFS法扩展为可计算多元函数的自适应采样法（ASM），并应用于FSS的电磁特性分析。文中首先建立FSS电磁特性分析模型以及散射参数的多元函数模型，其次基于Neville型拓扑关系分别给出一维和多维的自适应采样方法，最后通过算例分析，考察频率、入射方向等参数对FSS散射特性的影响，验证方法的有效性。

1 模型与方法

1.1 FSS电磁特性分析模型

具有L层介质衬底的平面FSS结构如图1所示 ，其中FSS位于第l与l＋1（l＝0，1，…，L）层介质界面。若频率为f的平面波沿方向（θi，φi）照射，则其导体表面的电场积分方程为

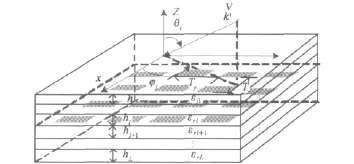
图1 平面波照射FSS

式中：Tx、Ty为FSS单元沿x、y方向排布的周期；分别为入射场和FSS结构的并矢格林函数；为导体未知感应电流。

采用矩量法求解未知电流可得到FSS的散射场，进而求得FSS的散射参数［11］。以TE极化传输系数为例，散射参数可表示为

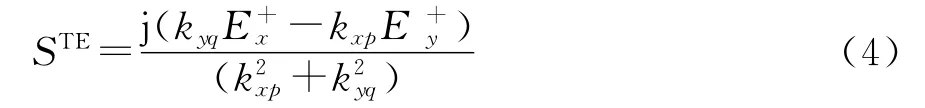
式中：E＋为介质衬底的透射场与FSS结构散射场之和。

由式（1）～（4）可以看出，FSS的散射参数与（θi，φi）、 f 和 FSS结构参数（周期，介质参数、厚度）等多个变量有关。因此，可定义n维变量空间Π＝（x1，x2，…，xn）并建立相应的散射参数函数S（x1，x2，…xn）.若令x1为f，建立一维函数S（x1）可获得FSS的频带响应 .若令x1、x2分别为θi、φi建立二维函数S（x1，x2），则可考察入射方向对散射特性的影响。为了获得多个变量在较宽范围内变化的FSS散射参数，需要采用矩量法反复计算电场积分方程，非常耗时。为此，引入ASM法来快速分析FSS的散射特性。

1.2 一维ASM法

对一维变量S（x0）建立有理函数模型

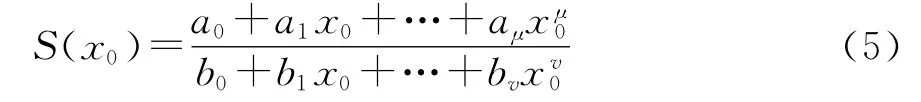
式中：μ、v分别为分子和分母多项式的阶数；a，b为未知系数。为了避免求解系数矩阵，采用递推拓扑技术Neville型算法［12］，如图2所示。

图2 Neville算法递推表

在递推关系中采用矩量法求解采样点x0i处的散射参数Si0（x0i）作为第一列初始值，递推关系从第二列开始，可选用以下三式建立

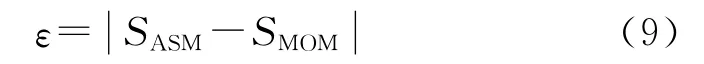
1.3 多维ASM法

对多元函数S（x1，x2，…，xn）建立有理函数模型

查找出现误差最大的点作为下一个可能的采样点，直至满足误差限ε，查找结束。选用不同递推关系可构造不同函数模型，当采样点足够多时，函数模型均能达到误差限范围。详细的递推关系选择方法参见文献［9］。为方便ε的选择，本文定义误差为目标函数模型的结果与电磁计算的结果之差为

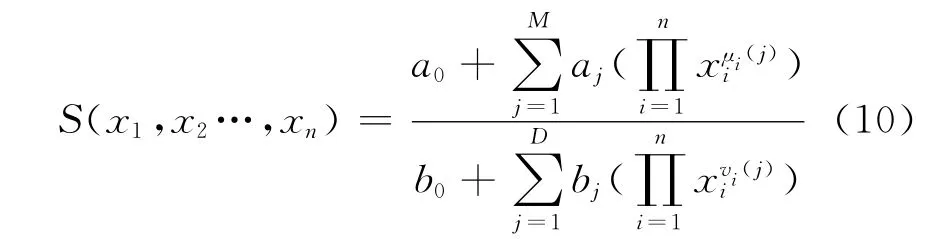
其中，μi（j）和vi（j）为整数函数，分别表示分子和分母中参数xi的次数，a、b为未知系数。为避免直接求解系数，将一维ASM法拓展为多维技术。定义为第i维空间的计算范围，ψi为第i维空间的测试点集合，Φi为第i维空间采样点集合，Ki为Φi内采样点个数，xik为Φi内采样点（k＝0，1，…，Ki－1）。初始化令各维空间的采样点不需要等间距分布，但必须完全填充空间网格，如图3所示。1）采样点查找

A：初始化多维空间的Φi和ψi，令i＝1；

B：固定第s维（s≠i）空间参数xs，选择Φs中各采样点，分别沿平行于xi方向进行一维ASM法查找最大误差εmax，如果εmax（）＜ε跳转到步骤4，否则，出现最大误差的测试点作为Φi的新采样点，令Ki加1，矩量法计算在Φs中各采样点的值以填充网格并作为下一步的初始值，i加1；

C：如果i≤n，重复步骤2，否则，令i＝1重复步骤2；

D：采样点查找结束，采样点网格已被完全填充，进行递推内插。2）递推内插

A：待求点为Q（x＊1，x＊2，…，x＊n），采样点的散射参数作为递推初始值，令i＝1；

B：固定第s维（s＝i＋1）空间参数xs，选择Φs中各采样点，分别沿平行于xi方向在x＊i点进行一维递推内插得到过度点（x＊1，x2，…，xn）的内插值，其中x2，…，xn分别为Φ2，…，Φn中的采样点，如图3所示，令i加1；

C：前一步过度点集合作为下一步计算的初始值，固定第s维（s＝i＋1）空间参数xs为Φs中各采样点，分别沿平行于xi方向在x＊i点进行一维递推内插得到过度点（x＊1，x＊2，…，xn），令i加1；

D：重复步骤3，直至i＝n，得到待求点Q（x＊1，x＊2，…，x＊n）.

图3 二维自适应采样内插法

2 数值结果

基于上述ASM法，分别对十字形贴片和方形孔径单元FSS的散射特性以及口径天线－FSS罩系统方向图进行计算，以验证算法的有效性。

2.1 十字形贴片单元FSS

十字形贴片单元如图4（a）示，单元尺寸为Ld＝6mm，Lw＝1mm，Tx＝Ty＝8mm .介质层结构如图1示，选择L＝3，l＝0，εr1＝εr3＝3，εr2＝1，h1＝h3＝0.2mm，h2＝10mm.图5给出了平面波垂直入射时，1～30GHz宽频内的频率响应。ε设置为10－5，频率采样点为21个。图6给出了以21GHz TE模式入射时，反射系数随θi从1°～80°，φi从0°～45°的变化规律，图中给出了φi分别为6°，16°和36°的三条曲线。ε设置为10－5，θi和φi方向的采样点分别为33、32个。由结果可以看出，采用ASM法可采集到特曲线上突变的点，计算的结果与直接MoM计算的结果完全吻合，计算量明显降低。

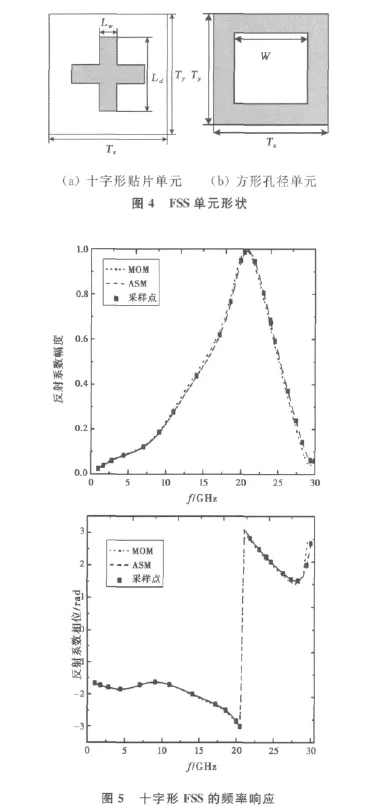
图6 十字形FSS的入射角度响应

2.2 方形孔径单元FSS

方形孔径单元如图4（b）示，单元尺寸Tx＝Ty＝16mm，W＝12mm.介质层结构如图1示，选择L＝2，l＝1，εr1＝εr2＝2.2，tanδ＝0.01，h1＝h2＝3.8 mm.ε设置为10－4，通过θi和φi方向21、20个采样点，可得到TE极化10GHz平面波照射下θi从1°～80°，φi同时从0°～45°变化的FSS传输系数幅度3D曲线图，如图7示。若θi和φi方向分别以1°为步长，采用直接MoM求解得到同样结果需要34个小时，但是采用多维ASM法仅用3.4个小时，计算效率明显提高。

2.3 FSS天线罩

以抛物柱面FSS天线罩为例，横截面外形方程为抛物线x2＝－a（z－hz），a为抛物线的焦距，hz为z向天线罩顶距原点的距离，柱面沿y方向长度为Ly，如图8所示。选择与图7相同的方形孔径FSS结构，单元分别沿y方向和横截面的母线方向周期均匀排布。天线罩外形参数为：a＝12λ，hz＝12λ，Ly＝36λ.

图9给出了坐标原点位置上工作频率为10 GHz的矩形口径面天线经过FSS罩的远区辐射方向图。其中FSS罩壁传输特性分别采用了直接MoM和ASM法计算，计算所需时间分别为90.4h、3.4h.图10（见845页）给出了罩面剖分单元位置上，采用ASM法计算FSS罩壁传输特性的误差分布。其中，TE、TM极化传输特性的均方误差分别为0.0943%，0.0347%，相对误差大于1%的天线罩剖分单元个数占总剖分单元个数的比例分别为0.2229%，0%.由结果可以看出，ASM法的计算精度满足工程要求，计算效率与直接MoM法相比提高了30倍。ASM法的计算时间与各维空间采样点数有关，正比于与剖分单元数无关；MoM法的计算时间与单元数成正比。通常情况下，工程FSS天线罩分析时罩面剖分单元上万个，计算中需要考虑不同频率、扫描角和极化因素，采用MoM法计算需要半年以上的时间，若采用ASM法进行整罩分析只需要1～2天的时间，计算效率显著提高。

3 结 论

提出了一种可快速分析多个变量对FSS散射特性影响的多维ASM法。对不同结构FSS单元及FSS罩的电磁特性进行了计算分析。计算结果表明：多维ASM法的计算结果与直接MoM法结果吻合，计算效率得到了明显改善。

文中主要针对FSS电磁特性随入射波频率、入射角变化的曲线进行计算分析，ASM法还可以应用于随介质厚度、介电常数、周期等参数改变FSS特性曲线的计算。

［1］MITTRA R，CHAN C H，CWIK T A.Techniques for analyzing frequency selective surfaces－a review［J］.Proceedings of IEEE，1988，76（12）：1593－1615.

［2］KIPP R A，CHAN C H.A numerically efficient technique for the method of moments solution for planar periodic structures in layered media ［J］.IEEE Transac－tion on Microwave Theory and Techniques，1994，42（4）：635－643.

［3］CHAN C H，MITTRA R.On the analysis of frequency selective surface using subdomain basis functions［J］.IEEE Transaction on Antennas and Propagation，1990，38（1）：40－50.

［4］CHUN Y，LU C C.Analysis of finite and curved frequency－selective surfaces using the hybrid volume surface integral equation approach［J］.Microwave and Optical Technology Letters，2005，45（2）：107－112.

［5］MARTINI E，CAMINITA F.Fast analysis of FSS radome for antenna RCS reduction［C］／／Antennas and Propag Society International Symposium IEEE.Albuquerque，9－14July 2006：1801－1804.

［6］童创明，张光甫，袁乃昌.维FSS电磁散射宽带特性的快速计算［J］.电波科学学报，2002，17（5）：441－444.TONG Cuangming，ZHANG Guangfu，YUAN Naichang.Fast calcula－tion of broadband electromagnetic scattering of one－dimensional frequency selective surfaces ［J］.Chinese Journal of Radio Science，2002，17（5）：441－444.（in Chinese）

［7］CHEN M S，WU Q.A new approach for fast solution of electromagnetic scattering problems over a broad frequency band［C］／／Microwave Antenna propagation and EMC Technologies for Wireless Communications 3rd IEEE International Symposium.Beijing，27－29 October，2009：932－934.

［8］LING J，XING S X.A novel two－dimensional ex－trapolation technique for fast and accurate radar cross section computation ［J］.IEEE Antennas and Wireless Propagation Letters，2010，9：244－247.

［9］DING Y，WU K L，FANG D G.A broad－band adaptive－frequency－sampling approach for microwave－circuit EM simulation exploiting Stoer－Bulirsch algorithm ［J］.IEEE Transaction on Microwave Theory and Technique，2003，51（3）：928－934.

［10］CHEN J Q，LIU Z W，CHEN R S.An adaptive frequency sampling method for frequency selective surface design exploiting Steor－Bulirsch algorithm ［C］／／Asia－Pacific Microwave Conference.Bangkok，December 11－14，2007：1－4.doi：10.1109／APMC.2007.4554968.

［11］WU T K.Frequency Selective Surface and Grid Array［M］.New York：John ＆ Wiley，1995.

［12］STOER J，BULIRSCH R.Introduction to numerical analysis［M］.Berlin：Spring－Verlag，1980.