多专家的PCA边缘检测模型

李建军，韦志辉，张正军

（1.南京理工大学理学院，210094 南京;2.南京理工大学 计算机科学与技术系，210094 南京）

多专家的PCA边缘检测模型

李建军1，韦志辉2，张正军1

（1.南京理工大学理学院，210094 南京;2.南京理工大学 计算机科学与技术系，210094 南京）

视一种边缘检测法为一个专家，为了解决不同专家检测结果的不一致性以及解决专家选择上的困难，提出了一种基于多专家与主成分分析(PCA)的边缘检测模型.首先给专家响应建立了统计模型，通过此模型分析得出，边缘检测模型能有效抑制专家噪声;然后利用提出的边缘检测模型融合多个专家的检测信息得到基于多专家的综合检测结果.实验结果表明，边缘检测模型可获得很好的边缘检测效果.

边缘检测;专家;主成分分析

数字图像处理自20世纪20年代至今，得到了很大的发展，图像处理技术也成功地应用于医学、生物学、国防、工业等广泛的领域.在图像处理过程中，每个处理步骤、处理方法都是多种多样，例如边缘检测，有基于滤波的方法［1－2］，也有基于模型的方法［3－4］，等等.这些方法各有优缺点，每种方法的处理结果也不尽相同，在没有一个客观标准对这些方法进行取舍的情况下，运用适当的方法对多个处理结果进行系统、客观、定量的综合分析，得到综合结果，解决处理结果的不一致性，是很有意义的工作.

1999 年，G.Hinton［5］将多个单一的模型以乘积的方式结合起来，提出了专家乘积模型.在这个模型中，每个专家都对所研究的数据进行了描述，但单个的专家更专注于描述数据的某个侧面特征，专家乘积模型则从多方面描述了数据，因此更富表现力.2005年，Roth［6］又将马尔科夫随机场模型与专家乘积模型结合起来，提出了专家场模型［7］，并在文献［8］中讨论了专家场在图像去噪等方面的应用.

主成分分析［9］是多元统计分析中比较成熟的多元统计分析方法，用于多维数据的降维，以降低数据分析的复杂度，它的应用十分广泛，包括数据压缩、图像处理和模式识别等等.主成分分析是通过投影的方法，将高维数据以尽可能少的信息损失投影到低维空间［10］.设X=(X1，X2，…，Xp)'为p维列向量，其协方差矩阵记为V，若V的秩为m(m ≤ p)，则存在 m 个主轴 wj，j∈ {1，2，…，m}，使得 Vwj= λjwj，其中wj为V的特征根 λj的特征向量.第j个成分定义为Yj=wX.记 Y=(Y1，Y2，…，Ym)'，则var(Y)是以V的特征根λj为对角线元素的对角阵，且

本文将专家的思想和主成分分析方法结合起来，提出了基于多专家与PCA的边缘检测模型.假设一种边缘检测法对应为一个专家，因为不同专家采用的思想和方法等的差异，会导致不同的边缘检测结果.由于缺乏选择的客观标准，很难确定该选择哪个专家来进行边缘检测.对多个专家的检测结果进行主成分分析，融合多专家的边缘检测信息，得到基于多专家的综合检测结果.这将解决不同专家检测结果的不一致性，并且在给专家响应建立统计模型的基础上，通过理论分析得出，本文提出的边缘检测方法能有效抑制专家噪声.实验证明，利用本文提出的边缘检测模型得到的边缘检测效果是令人满意的.

1 基于多专家的边缘检测模型

1.1 专家响应模型与分析

式中 εi为专家噪声，且令 εi～ N(μi，σ2).设 E 与εi相互独立，且 εi，(i=1，2，…，p)相互独立.因为成分Yj=w'jX，记 wj=(wj1，wj2，…，wjp)'，即有

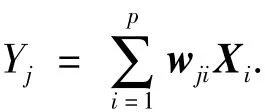
则Yj的方差为

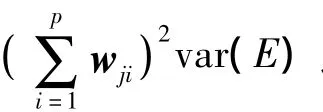
1.2 边缘检测模型

每一个专家响应Xi都包含了图像I的边缘信息，本文希望融合这些信息得到综合的边缘检测结果.

协方差阵V的非零特征根λ1，λ2，…，λm描述了数据的信息分布，称

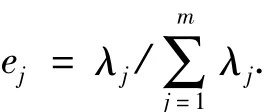
为成分Yj的贡献率，称

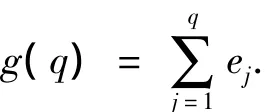
为累计贡献率，这里1≤q≤m.

为了保留原数据的信息，又要达到降维的目的，采用累计贡献率的大小来决定q的值.令

式中:T为给定的门限值;q*为选择成分的个数.当q*确定后，称 Y1，…，Yq*为主成分，Yq*+1，…，Ym为弱成分.通常T取85%，此时利用主成分可以足够好的恢复原数据的信息，且能起到降维与抑制专家噪声的目的.本文给出基于多专家的综合边缘检测结果为

2 实例与分析

不失一般性，在此采用常用的5种边缘检测算子来检测边缘，这5种算子即5个专家，它们分别为 Roberts算子、Sobel算子、Prewitt算子、LoG算子和Canny算子.

2.1 实例:基于多专家的边缘检测

图1(a)为cameraman图像原图，图1(b)～(f)分别为上述5个专家检测出的边缘结果.从图1中可看出，这些专家检测出的结果类似，但也各有特点.Roberts算子、Sobel算子、Prewitt算子检测出来的结果更相似，而Canny算子和LoG算子则能检测出更多的边缘.

图1 单个专家检测结果

本文利用主成分分析的方法对5个专家的检测结果进行主成分分析.按贡献率从大到小得到的第1主成分～第5主成分如图2所示.

图2 主成分分析结果

图2(b)～(f)的贡献率分别是53.011%、20.095%、16.104%、10.015%和0.773 78%.从图2中可看出，图2(b)～(f)包含的图像细节越来越少，也即包含的图像边缘信息越来越少.取T=85%，由式(1)融合主成分的信息得到综合的边缘检测结果，如图3所示.

图3 基于多专家的检测结果

从图3可看到，由基于多专家边缘检测法检测出的边缘结合了各个专家检测的边缘信息，相比Roberts算子、Sobel算子、Prewitt算子的检测结果，基于多专家的检测结果有更多的边缘细节，相比Canny算子和LoG算子的检测结果，基于多专家的检测结果检测的边缘更细腻.

2.2 分析

通过上述实例可看出，基于多专家与PCA的边缘检测法具有下列特点.

1)它是多个专家边缘检测结果的综合.

由于不同专家采用的思想、方法等的不同，导致了不同的边缘检测结果，但很难确切地判断哪个专家好或是不好.基于多专家的边缘检测方法提供了一个客观的、定量的分析方法，将这些专家的处理结果综合起来，得到较为理想的综合结果，解决了处理结果的不一致性.

2)它保留了多个专家边缘检测结果的主要信息，同时又能有效抑制专家噪声对检测结果的影响.

每个专家在进行边缘检测任务时都有其优劣之处，其检测的结果包含了该专家带来的噪声.基于多专家的边缘检测法对这些结果进行了主成分分析，然后对成分进行取舍，既保留了图像的主要边缘信息又降低了专家噪声对检测结果的影响.实验证明，综合的检测结果是令人满意的.

3 结论

本文引入专家的思想，将每个边缘检测方法视为一个专家，在给专家响应建立了概率统计模型的基础上，从理论上分析了提出的基于多专家与PCA的边缘检测模型能有效抑制专家噪声.此模型解决了各个专家检测结果的不一致性，也解决了专家选择上的困难.实验证明，采用此模型能减小单个专家对检测结果的影响，能得到令人满意的边缘检测效果.本文的处理方法也可用于其他图像处理问题，如图像分割等.

［1］GONZALEZ R C，WOODS R E.Digital Image Processing ［M］.2nd ed.Englewood Cliffs:Prentice－Hall，2002.

［2］ZIOU D，TABBONE S.Edge detection techniques－an overview ［J］.Pattern Recognition and Image Analysis，1998，8(4):537－559.

［3］TARDÓN L J，BARBANCHO I，MÁRQUEZ F.A markov random field approach to edge detection［C］//Proceedings of the Mediterranean Electrotechnical Conference 2006.Piscataway:IEEE，2006:482－485.

［4］KONISHI S，COUGHLAN J M，YUILLE A L，et al.Statistical edge detection:learning and evaluating edge cues［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2003，25(1):57－74.

［5］HINTON G.Product of experts［C］//Proceedings of the 9thInternational Conference on Artificial Neural Networks 1999.Stevenage:IEEE，1999:1－6.

［6］CROSS G，JAIN A.Markov random field texture models［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1983，5(1):25－39.

［7］ROTH S，BLACK M.Fields of experts:a framework for learning image priors［C］//Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition.Los Alamitos:IEEE，2005:860－867.

［8］ROTH S，BLACK M.Fields of experts［J］.International Journal of Computer Vision，2009，82(2):205－229.

［9］JOLLIFFE I T.Principal Component Analysis［M］.New York:Springer－Verlag，1986.

［10］HOTELLING H.Analysis of complex of statistical variables into principal components ［J］.Journal of Educational Psychology，1933，24(6):417－441.

Edge detection model based on multi-expert and principal component analysis

LI Jian－jun1，WEI Zhi－hui2，ZHANG Zheng－jun1

(1.School of Science，Nanjing University of Science and Technology，210094 Nanjing，China;2.Dept.of Computer Science and Technology，Nanjing University of Science and Technology，210094 Nanjing，China)

Each method of edge detection is regarded as an expert.To solve the problem of inconsistency of different expert responses and the difficulty of choosing right expert，a model of edge detection based on multiexpert and principal component analysis(PCA)is proposed.Firstly，a statistical model for expert response is established，and theoretical analysis shows that the edge detection model can effectively suppress noise coming from the expert.Then，the information of multiple detection results were combined to obtain the general detection result with the model based on multi－expert and PCA.The experimental results are very satisfactory.

edge detection;expert;principal component analysis

TP391

A

0367－6234(2012)11－0092－04

2011－10－30.

国家高技术研究发展计划资助项目(2007AA12Z142);国家自然科学基金资助项目(60874118).

李建军(1975—)，男，博士研究生;

韦志辉(1963—)，男，教授，博士生导师.

李建军，j－jli@163.com.

(编辑 张 红)