深空着陆器对偶控制策略

高 艾，崔平远，，崔祜涛

（1.北京理工大学深空探测技术研究所，100081 北京;2.哈尔滨工业大学深空探测基础研究中心，150001 哈尔滨）

深空着陆器对偶控制策略

高 艾1，崔平远1，2，崔祜涛2

（1.北京理工大学深空探测技术研究所，100081 北京;2.哈尔滨工业大学深空探测基础研究中心，150001 哈尔滨）

以深空着陆任务为背景，针对视觉导航过程中由于有限观测能力引起的估计性能不佳问题，研究了一种深空着陆器对偶控制策略.该策略将导航估计不确定性引入系统状态，给出包含与估计方差相关的二次型性能指标评价方法，利用着陆状态可观测性与着陆轨迹之间的耦合特性，合理优化观测轨迹，克服着陆过程中可观测性缺乏问题，大幅度提高系统的导航估计性能，使深空着陆器导航制导控制整体性能得到保障.

深空探测软着陆;自主GNC技术;非线性耦合;对偶控制

深空着陆过程中，由于着陆器受到各种不确定性因素影响，其制导控制律的设计必须建立在对系统状态最优估计的基础上，这使得精确的导航定位显得尤为关键;加之着陆时间较短，深空环境中通信延迟时间较长，基于地面站的导航制导控制模式不再适用，因此发展深空着陆自主实时精确的导航制导控制策略已成为目前国内外学者研究的热点.

传统的制导控制设计过程是基于确定性等价假设，其制导控制策略的选取与导航估计不确定性互不影响，从而可将系统的导航制导控制设计分为两个独立的过程，即利用导航滤波器从噪声污染测量中估计出系统状态;再假设这样的估计状态即为系统的真实状态，利用传统的制导控制技术给出到达目标着陆区域所需的控制量.由于这种方法简便易行且运算量低，因此成为以往着陆段任务制导控制策略的选择［1－2］.

然而，对于非线性的着陆器系统而言，其可观测性与状态轨迹间存在非线性耦合，因此其可观测性会受到系统状态轨迹的影响［3］.当观测能力受到限制时，有限的观测能力会导致缺乏状态观测的估计性能不佳，进而弱化制导控制性能，尤其对于具有不规则引力场特性的小行星着陆制导控制而言，一个很小的控制偏差会导致最终着陆器与目标着陆点的大范围偏离，达到可靠的着陆性能就变得极具挑战性.因此，利用尽可能少的导航敏感器，通过优化观测轨迹，在满足着陆任务要求的同时，尽可能地减小导航定位误差，从而提高导航制导控制系统的整体性能是深空着陆过程中亟待解决的问题.

为了使这类非线性系统达到更好的控制性能，A.A.Feldbaum［4－6］首先提出了对偶效应的概念，指出控制输入具有双重性目的:一是达到系统稳定的控制目标;二是改善系统状态估计信息.二者紧密耦合而不能分离，这种耦合导致了无法获得最优控制的解析解.自此以后，国内外学者针对这一主题开展了大量的研究工作，并已获得一些简单问题的最优解.J.Sternby［7］解决了四状态马尔科夫链问题;B.Bernbardsson［8］处理了具有双增益的一阶系统.此外，还求得了一些简单的自适应对偶控制问题的代数解［9］.然而，已得到解决的问题仅是特例，那些具有合理规模的问题几乎都是既无解析解又无数值解的不可解问题.处理某些对偶特性的多种次优技术［10－11］，同时被发展应用于自适应控制和随机控制.对于更特殊的物理背景应用——采用单角度测量的导弹拦截备受关注，多个不同的对偶控制制导律被提出［12－13］.这些技术分别通过加入扰动信号、约束估计量变化、修正代价函数和利用有限参数逼近价值函数等手段提供问题的近似解.其中存在两种相对简单和直观的方法:1)增加一个试探性的控制输入以改进系统状态的可观性.这种方法简单易行，附加控制输入可与确定性控制输入的设计过程分离开，由一系列启发式方法独立完成，但在设计流程中缺乏系统性方法且整体性能严重依赖于启发式方法的选取;2)构造代价函数，该代价函数是标准代价函数与系统误差方差标量函数的加权.这种方法的优点在于可直接应用数值搜索技术进行求解，然而其搜索空间会随时间呈指数增长，因此求解问题相当有限.同时，代价加权系数的选取同样缺乏系统性方法，这会导致最终构造的代价函数与实际代价相距甚远.

本文以基于单目视觉导航的深空着陆制导控制任务为背景，考虑有效控制与可靠估计间的对偶问题，通过扩展状态空间将系统不确定性作为部分代价引入二次型性能指标中，从而采用简便易行的线性二次型控制技术给出随机优化反馈控制律.该对偶控制策略利用非线性系统可观测性与状态轨迹间存在的非线性耦合关系来克服着陆过程中可观测性缺乏的问题，通过合理地优化着陆器下降轨迹，大幅度提高系统的导航估计性能，使深空着陆器导航制导控制整体性能得到保障.

1 系统建模

定义着陆点固连坐标系Σl:ol-xlylzl，该坐标系原点ol位于预定的着陆点，olzl轴与行星质心指向着陆点矢量oiol方向一致.olxl沿经线的切线方向指向南极方向，olyl与olxl、olzl之间满足右手法则，如图1所示.

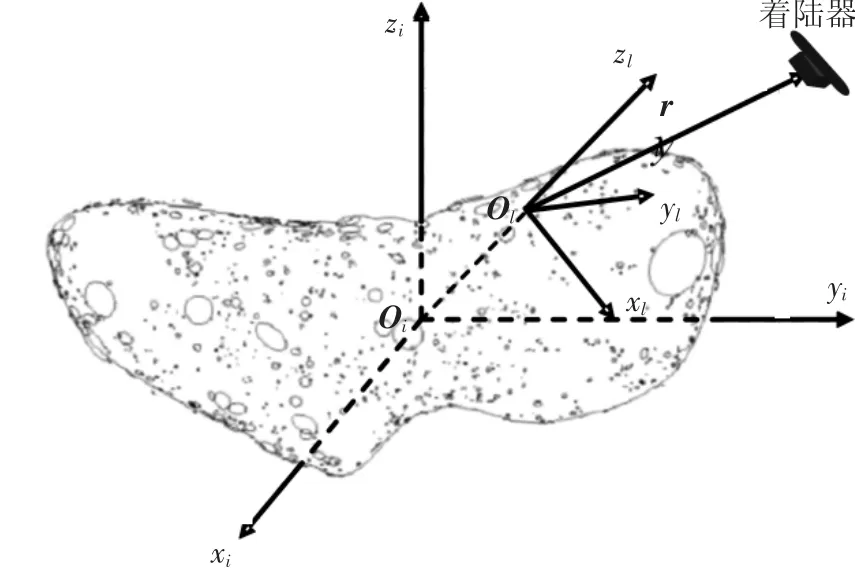
图1 坐标系定义

图1中坐标系Σi:oi-xiyizi为行星中心惯性坐标系，其原点在行星的质量中心，zi轴沿行星最大惯量轴方向，xi轴沿历元时刻行星最小惯量轴所指方向，yi轴与xi轴、zi轴之间满足右手法则.

在着陆点固连坐标系下建立探测器动力学方程

式中:r，v分别为着陆器相对于预定着陆点的位置矢量与速度矢量;u为控制加速度;g为行星引力加速度;ae，ak分别为由行星自旋所引起的离心惯性加速度与科氏加速度;aΔ为未建模加速度.

将式(1)中的加速度项－ae－ak+aΔ作为系统过程噪声处理，得到如下动力学模型

式中:x=［r v］T为着陆器状态;Er=［I0］为系数矩阵;A= ［［0 0］T［I0］T］为系统矩阵;B=［0 I］T为输入矩阵，ω =－ae－ak+aΔ为系统过程噪声.

这里采用基于单目视觉矢量测量的光学相对导航方案，选择着陆点固连坐标系下探测器的位置矢量作为观测量，则观测模型为

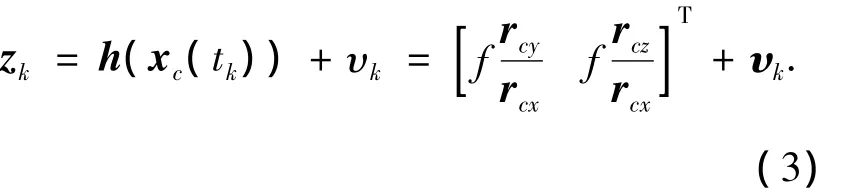
式中:rc=Cclr= [rcxrcyrcz]T为探测器相对于目标着陆点的位置矢量在相机坐标系下的投影;Ccl为着陆点坐标系与相机坐标系之间的转换矩阵;υk为光学导航观测噪声.

2 随机优化反馈对偶控制算法

对于线性系统，可观测性仅依赖于系统动力学和观测模型.然而，对于非线性系统而言，由于可观测性与状态轨迹间存在非线性耦合，因此其可观测性会受到系统状态轨迹的影响.实际上，如果系统是动态可观的，可以利用这种耦合来克服可观测性的缺乏，从而达到更好的估计性能.

尤其对式(2)和式(3)描述的基于单目视觉导航控制的软着陆过程而言，通过合理地规划着陆器下降轨迹可以大幅度提高系统的可观性.然而，如何在众多可行轨迹中计算出最优轨迹是一个富有挑战性的随机优化任务.由于有效控制与可靠估计间权衡问题的复杂性，普遍应用的确定性等价控制技术和其他多种近似技术在该问题的处理中受到限制［14］.这里考虑了该权衡问题的新的对偶控制算法，该算法将系统不确定性作为部分代价引入性能指标中，并应用线性二次型控制技术给出反馈控制率，进而通过对深空着陆下降轨迹的随机优化，在满足着陆任务要求的同时，尽可能地减小导航定位误差，从而提高导航制导控制系统的整体性能.

将着陆器状态x描述为分布在状态空间中的粒子云 xi(i=1，2，…，N)，期望状态 xd与每个粒子xi之间距离的平方和作为代价函数用于优化.这一代价反映了粒子与期望状态间的距离以及其分散程度.在某一特定时刻的控制性能可用二次型表达式描述为

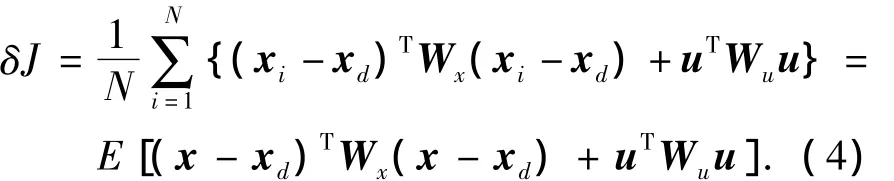
式中:Wx为状态偏差权重矩阵;Wu为控制燃耗权重矩阵.

则式(4)可整理为

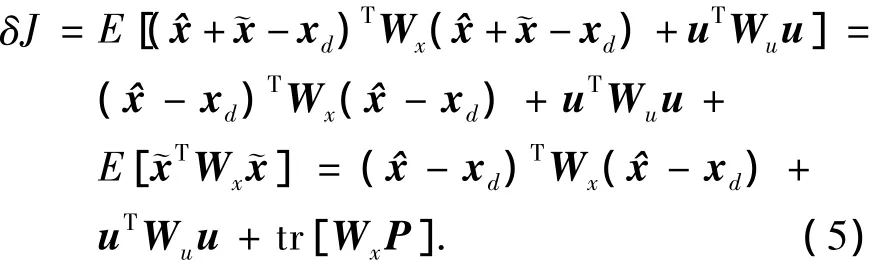
式(5)中前2项为典型的二次型，如果能将第3项描述为二次型形式，则可以利用现有的数学工具对问题进行求解.注意到误差方差阵P为非负定矩阵，由矩阵理论可知，对称的非负定矩阵P ∈R6×6可分解成P=SST，其中S∈R6×6为下三角阵，由P唯一确定，即矩阵P的下三角分解平方根阵为

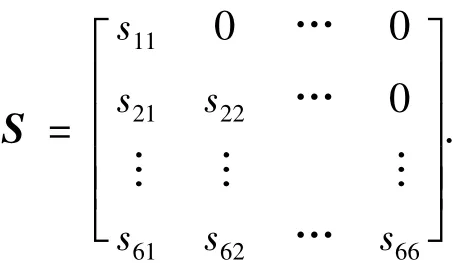
为便于后记，设Wx为一对角阵，且Wx(i，i)=wii(i=1，2，…，6)，则式(5)中最后一项可整理为

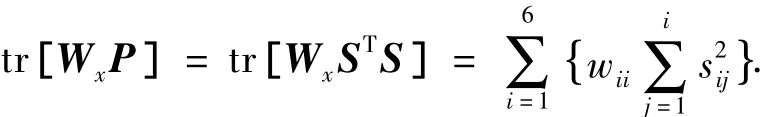
进而，式(5)可改写为

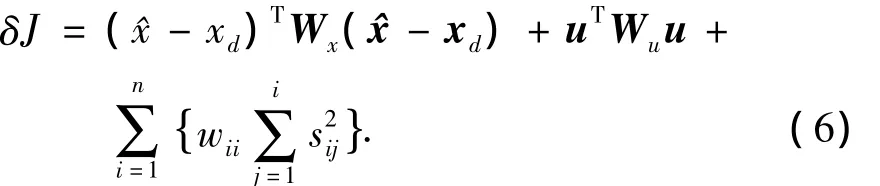
将式(6)对时间积分作为随机优化的性能指标为

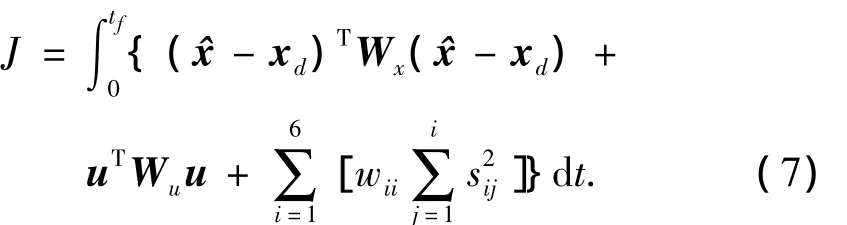
式(7)中前2项对应于确定性等价控制代价，第3项对应于系统不确定性代价.

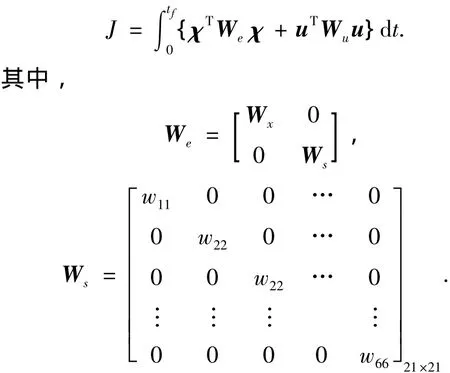
综上所述对于深空着陆器下降轨迹优化问题可描述如下:

1)对于系统的扩展状态空间描述为

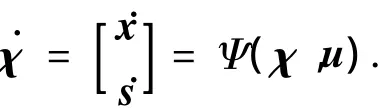
2)在时间区间［0，tf)上寻找最优控制输入u*，满足

由于涉及协方差传播和扩展空间描述的复杂性，寻求非线性控制系统的最优解十分困难.这里采用无限时长稳态增益状态反馈控制技术获得优化问题的次优解.

假设对于优化问题(8)存在矩阵Γ满足代数Riccati方程为

则反馈控制率有如下形式

式中:χss=［xdsss］T为扩展系统稳态解;Kx主要侧重于稳定控制目标;Ks提供附加反馈控制用于削弱系统的不确定性，从而提高控制性能.

3 数学仿真分析

以小行星Eros433作为目标天体，其自旋角速度为1 639.4(°)/d，名义半径为16 km，引力常数为4.462 1×105m3·s－2，在仿真中采用其四阶引力场模型.在着陆点固连坐标系下，探测器初始位置为［500 20 －50］Tm，相对小行星表面速度为［1.5 2.0 0］Tm·s－1，预期着陆时间300 s.

考虑着陆器初始状态估计误差，其位置初始估计误差与速度估计误差分别服从方差为100 m2和0.1 m2·s－2的随机分布时，利用传统制导控制算法对着陆器进行前馈控制，在预期着陆时间内着陆器最终着陆速度高达3 m·s－1，在期望着陆时间内存在撞入目标天体的危险，如图2所示.这主要是由于探测器状态的可观测性受系统状态轨迹的影响，当观测能力受到限制时，导航估计误差将持续增大，且其制导控制性能会随着导航误差的增大被大幅度弱化，如图3所示.

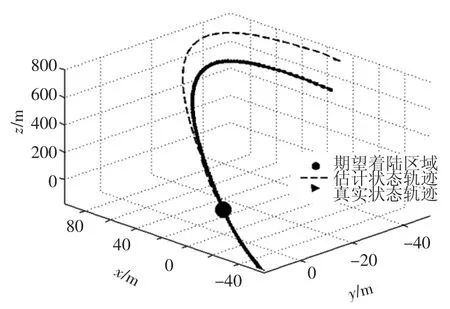
图2 传统制导控制下着陆器下降轨迹

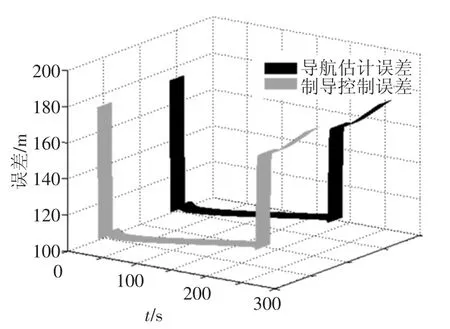
图3 导航估计性能与制导控制性能对比

考虑导航估计误差的存在，在行星着陆控制过程中加入本文设计的反馈对偶控制对着陆轨迹进行随机优化，由图4可见，探测器的估计误差随着下降轨迹的变化在不断减小，末端着陆器真实状态与前馈制导所产生的路径点基本相符，其最终着陆位置偏差在5 m范围内，速度偏差在0.05 m·s－1左右.由图5给出的导航偏差与制导控制偏差的变化趋势，可看出通过反馈对偶控制对前馈制导给出的下降轨迹的随机优化作用使导航与制导控制性能得到了整体提高.

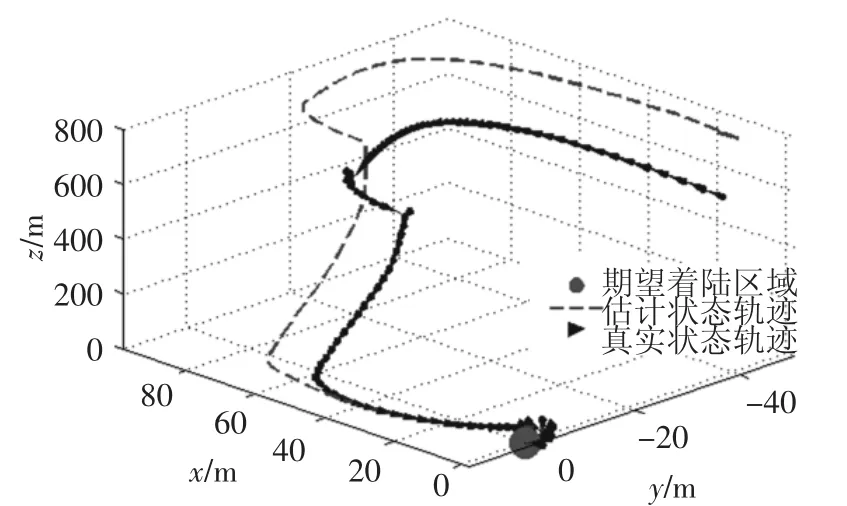
图4 随机优化反馈对偶控制下着陆器下降轨迹

观察导航误差与着陆器水平运动情况的关系，如图6和图7所示，可发现前馈制导给出的水平运动规划十分平滑，特别是着陆末端着陆器在水平运动方向几乎无变化，导航性能随着规划轨迹逐渐变差;而通过加入反馈对偶控制随机优化后的观测轨迹在水平运动方向变化剧烈，导航性能逐步提高.可见，反馈对偶控制通过增加着陆器的水平运动，对运动轨迹进行随机优化，提高了系统状态的可观测性.进一步对比其控制燃耗与整体优化性能指标，如图8中数据显示，尽管加入反馈对偶控制后系统控制燃耗增加，但其总体性能得到了102量级的提升.

图5 导航估计性能与制导控制性能对比

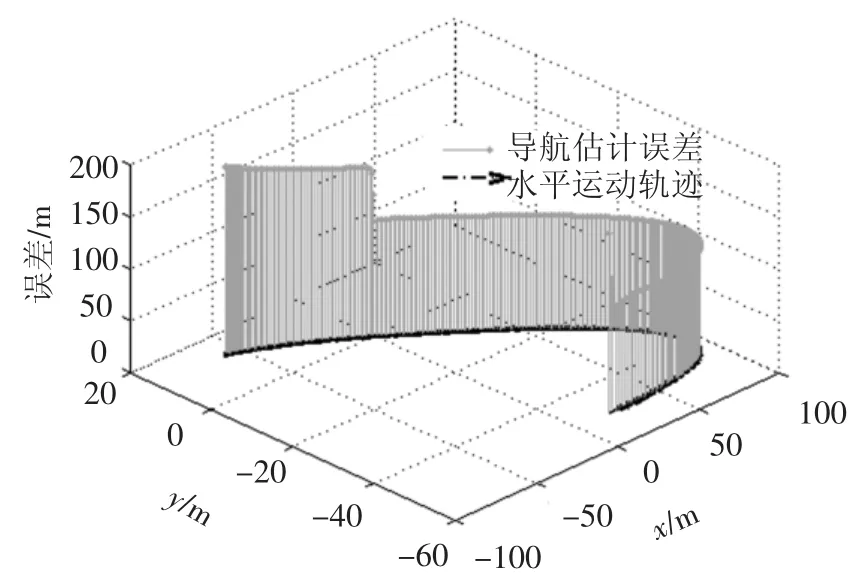
图6 传统制导控制下着陆器水平运动趋势对导航误差的影响

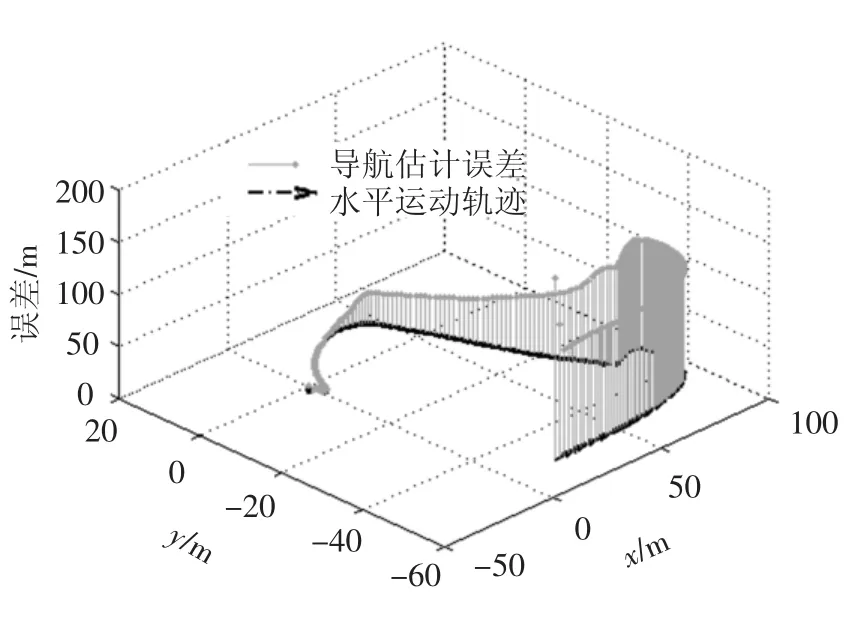
图7 反馈对偶控制下着陆器水平运动趋势对导航误差的影响

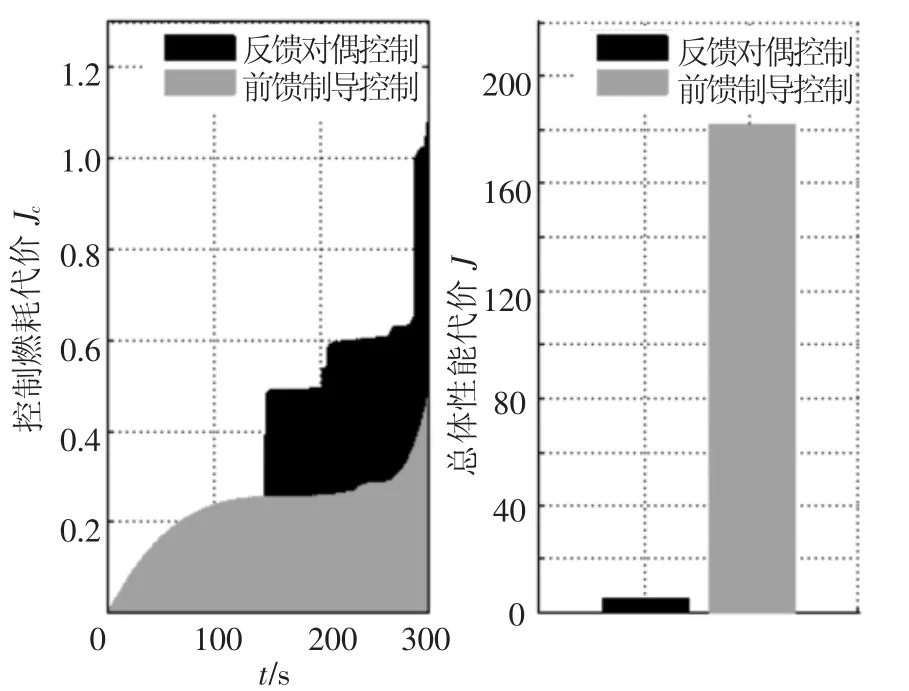
图8 控制燃耗与总体性能对比

4 结论

1)针对视觉导航过程中由于有限观测能力引起的估计性能不佳问题，研究了一种深空着陆器对偶控制策略，利用非线性系统可观测性与状态轨迹间存在的非线性耦合关系来克服着陆过程中可观测性缺乏的问题.

2)利用着陆过程中着陆状态可观测性与着陆下降轨迹之间的耦合特性，将导航估计不确定性引入并扩展系统状态，给出包含与估计方差相关的二次型性能指标评价方法，使复杂优化问题的求解变为线性二次型最优控制的求解，避免了动态规划与基于搜索方法的运算负担.

3)通过进一步的仿真分析可知，该随机优化方法以控制燃耗为代价，通过对标称轨迹的合理优化，在满足着陆任务的同时，使导航估计性能大幅提高，从而使系统整体性能得到提升，达到可靠着陆行星的最终目标.

［1］KLUMPP A R.Apollo lunar descent guidance［J］.Automatica，1974，10(2):133－146.

［2］SOSTARIC R R，REA J R.Powered descent guidance methods for the moon and mars［C］//Collection of Technical Papers－ AIAA Guidance，Navigation，and Control Conference.San Francisco，USA:American Institute of Aeronautics and Astronautics Inc，2005:4495－4514.

［3］METTHIES L，KANADE T，SZELISKI R.Kalman filter-based algorithms for estimating depth from image sequences［J］.International Journal of Computer Vision，1989，3(3):209－238.

［4］FELDBAUM A A.Dual control theory I-II［J］.Automation and Remote Control，1960，21(9):874 －880，1033－1039.

［5］FELDBAUM A A.Dual control theory III-IV［J］.Automation and Remote Control，1961，22:1－12，109－121.

［6］TSE E，BAR-SHALOM Y，MEIER L.Wide-sense adaptive dual control for nonlinear stochastic systems［J］.IEEE Transactions on Automatic Control，1973，AC－18(2):98－108.

［7］STERNBY J.A simple dual control problem with an analytical solution［J］.IEEE Transactions on Automatic Control，1976，21(6):840 －844.

［8］BERNHARDSSON B.Dual control of a first-order system with two possible gains［J］.International Journal of Adaptive Control and Signal Processing，1989，3(1):15－22.

［9］ASTROM K J，WITTENMARK B.Adaptive Control［M］.2nd ed.Boston，MA:Addison-Wesley Longman Publishing Co Inc，1995:365 －370.

［10］WITTENMARK B.Adaptive dual control methods:an overview［C］//Adaptive Systems in Control and Signal Processing 1995.A Postprint Volume from the 5th IFAC Symposium.Oxford，UK:Pergamon，1995:62－72.

［11］UNBEHAUEN H.Adaptive dual control systems:a survey［C］//Proceedings of the IEEE 2000 Adaptive Systems for Signal Processing，Communications，and Control Symposium(Cat.No.00EX373).Piscataway，NJ:IEEE，2000:171－180.

［12］CASLER R J.Dual-control guidance strategy for homing interceptors taking angle-only measure-ments［J］.JournalofGuidance， Control， and Dynamics， 1978，1(1):63－70.

［13］HULL D G，SPEYER J L，BURRIS D B.Linear-quadratic guidance law for dual control of homing missiles［J］.Journal of Guidance，Control，and Dynamics，1990，13(1):137－144.

［14］BRYSON A E，HO Y C.Applied Optimal Control［M］.Hemisphere，New York:Taylor ＆ Francis，1975:131－141.

［15］JULIER S J，UHLMANN J K.Unscented filtering and nonlinear estimation［C］//Proceedings of the IEEE.Piscataway，NJ:IEEE，2004:401－422.

［16］MERWE R，WAN E A.The square-root unscented Kalman filter for state and parameter estimation［C］//2001 IEEE InternationalConference on Acoustics，Speech，and Signal Processing.Proceedings(Cat.No.01CH37221).Piscataway，NJ:IEEE，2001:3461 －3464.

Dual control strategy of planetary lander

GAO Ai1，CUI Ping-yuan1，2，CUI Hu-tao1，2

(1.Institute of Deep Space Exploration Technology，Beijing Institute of Technology，100081 Beijing，China;2.Deep Space Exploration Research Center，Harbin Institute of Technology，150080 Harbin，China)

For landing on planet，a dual control strategy is developed to solve the problem of poor estimation performance which results from the lack of observability.The system uncertainty is incorporated into the quadratic performance index as a cost by extending state space，which takes advantage of the nonlinear coupling between observability and trajectory to overcome the lack of observability and to achieve better estimation performance.By stochastic optimizing the landing trajectory，the overall performance of GNC system for landing on planets is improved.

soft landing for deep space exploration;autonomous GNC technology;nonlinear coupling;dual control

V448.233

A

0367－6234(2012)11－0075－06

2012－02－13.

国家自然科学基金资助项目(60874094);国家高技术研究发展计划资助项目(2010AA122206).

高 艾(1984—)，女，博士，讲师;

崔平远(1961—)，男，教授，博士生导师;

崔祜涛(1970－)，男，教授，博士生导师.

高 艾，gaoai@bit.edu.cn.

(编辑 张 红)