一种具有模糊时间参数的离散事件仿真方法
黄镇谨,陈 波,欧阳浩
( 广西工学院 计算机工程系,柳州 545006)
0 引言
传统的离散事件仿真方法要求在仿真过程中获得系统的精确信息,如系统中各随机变量的概率分布和参数等。实际中这些信息往往难以精确的获得。经典的随机服务系统中一般假设顾客到达时间及服务时间服从特定的分布函数。实际应用中要获得参数的分布特性,需要对系统参数进行大量的数据采样并采用拟合的方式获得其分布规律,这不仅费时费力,而且很多时候得到的结果与理论上的分布函数具有比较大的偏差。利用这些具有一定偏差的分布函数对系统进行分析虽然能够带来解析处理的方便,但在一定程度上牺牲了系统的真实性和实际应用价值。因此,需要另外的手段处理这些不精确的信息。采用模糊数描述信息的不精确性是一种可行办法。
离散事件仿真的核心是对事件与其仿真时钟的处理[1]。事件以事件列表的形式存在,时间的推进与其状态的更新取决于下一个事件的发生时间。事件列表的更新随着系统状态的演化不断进行。当前仿真时间由仿真时钟维护,在每一个事件发生时更新系统仿真时钟。引入模糊数后,事件的发生与其仿真时钟的更新时间不再是精确的数值,而是一个区间值,区间中的每一个数值具有相应的隶属度。参数模糊化后的离散事件仿真中,事件的选择与其仿真时钟的更新比基于概率分布仿真复杂,多个模糊数之间的排序结果可能并不唯一。因此一个好的模糊仿真模型应该具有以下两个属性[2]:首先模型应该能够再现每一种可能的状态演化,其次,模型不能引入实际运行中不可达状态。
离散事件仿真中引入模糊数据后由于事件的发生时间具有模糊的值,因此需要对后续的可选择事件集进行排序,然后从中选择符合要求的事件作为下一个将要发生的事件。虽然把模糊数学引入离散事件系统仿真的概念并不难想到,但是由于处理模糊信息的方法和过程与处理精确信息有较大的不同,因此这个领域中提出的方法还比较有限。文献[3]提出了基于积分值的模糊仿真方法。在文献[4]中,一种基于预期存在度量(expected existence measure EEM)的模糊排序方法被应用于离散事件仿真中,在此基础上,Grieco等提出了一种对模糊事件进行切割以调整该问题的方法[5],文献[6]利用模糊数与上下确界的距离来确定其大小。在这四种方法中,前三种方法都不能同时满足离散事件仿真的两个属性,最后一种方法其待定参数的确定比较复杂。文献[7]从可能性空间及区间分析的角度探讨具有模糊输入参数的离散事件系统仿真问题,该方法模糊化的对象是分布函数中的参数而不是输入参数本身,因此仍然面临需要大量的数据采样并拟合分布函数的问题。
针对以上问题,在文献[4]的基础上,本文提出一种新的方法,根据前一个事件结束时的当前时刻与其另一个待定参数确定下一个将要发生的事件 (two independent parameters TIP,以下简称TIP法)。该方法避免了概率方法的数据采集和拟合分布函数问题,通过模糊数的预选择降低了模糊数排序的复杂度,与现有模糊离散事件仿真方法相比,在不引入不可达状态情况下能再现系统演化的所有状态。
1 积分值法和EEM法
基于积分值和EEM的方法都是将具有一定区间取值的模糊集或模糊数的比较转换成确切值后再进行比较,采用一个待定参数确定模糊数的大小顺序。由于本文给出的方法中与这两者有关,下面简要介绍这两种方法。设事件E发生时间为符合隶属度函数μ(x)的模糊集F(x),令gL(x), gR(x)为 μL(x), uR(x)的反函数,积分值定义如下[3]:
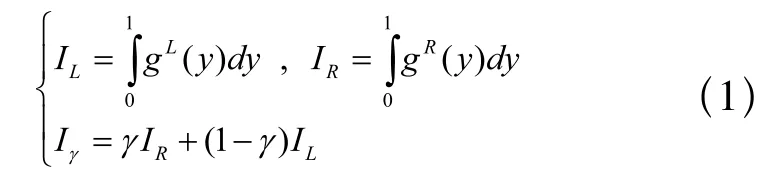
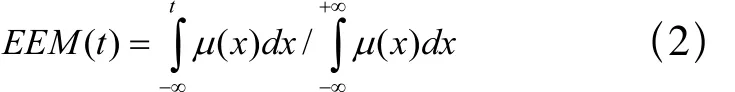
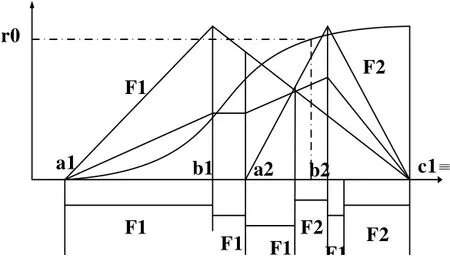
令 EEM(t)=r,给定 r∈ [0,1],t=EEM-1(r),根据t值的大小对模糊集F(x)进行排序。图1给出了两个具有重叠关系的梯形模糊集F1(a1,b1,c1,d1)、F2(a2,b2,c2,d2)的积分值和EEM。
在图1中,模糊集F1有可能大于或小于模糊集F2,采用前述两种方法进行排序时,对于r∈[0,1],都有F1<F2,因此基于积分值和EEM的方法不能再现系统的每一种可能的演化状态。令b=c,则可以采用同样的方式处理三角形模糊数。
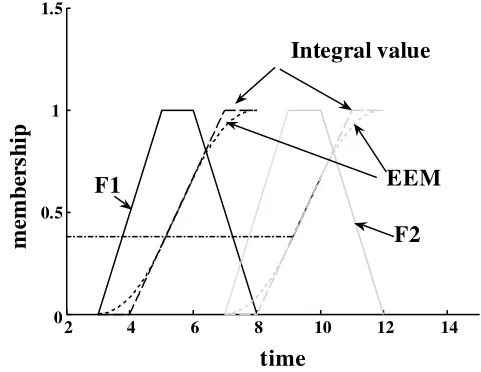
图1 积分值法和EEM法
2 TIP方法
2.1 模糊数预选择
事件的处理和仿真时钟的更新是离散事件仿真中两个关键的问题,实际上,对仿真时钟的更新是与事件的处理相关的。例如,令模糊数Tnow表示当前的仿真时刻,事件E为下一个将要发生的事件,与E相对应的活动延迟时间为模糊数TE,处理完前一个事件后,仿真时钟被推进到Tnext=TnowTE处。因此如何选择下一个将要发生的事件是离散系统仿真中的核心。模糊仿真中,时间标记不再是确定的,而是具有一定区间的模糊数。通过对模糊数进行排序确定大小从而选取下一个要发生的事件。
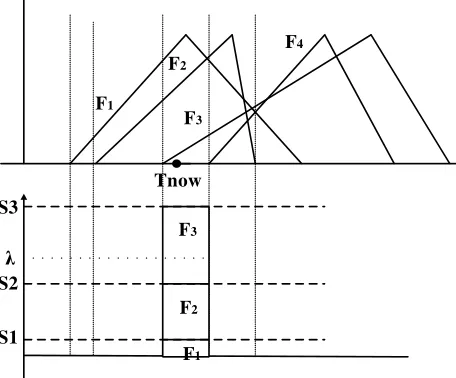
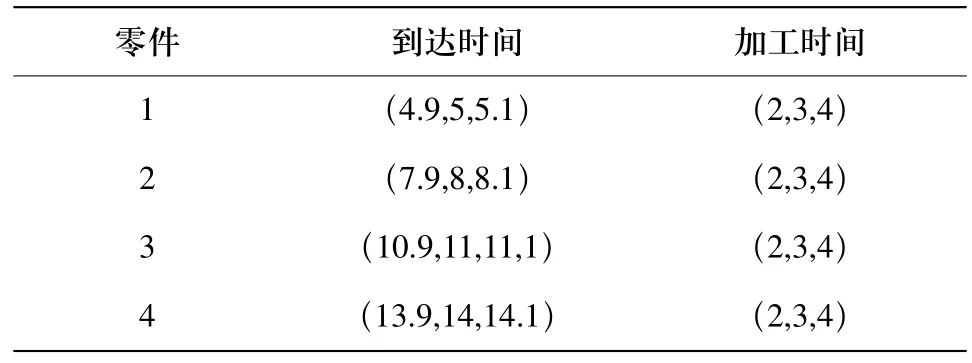
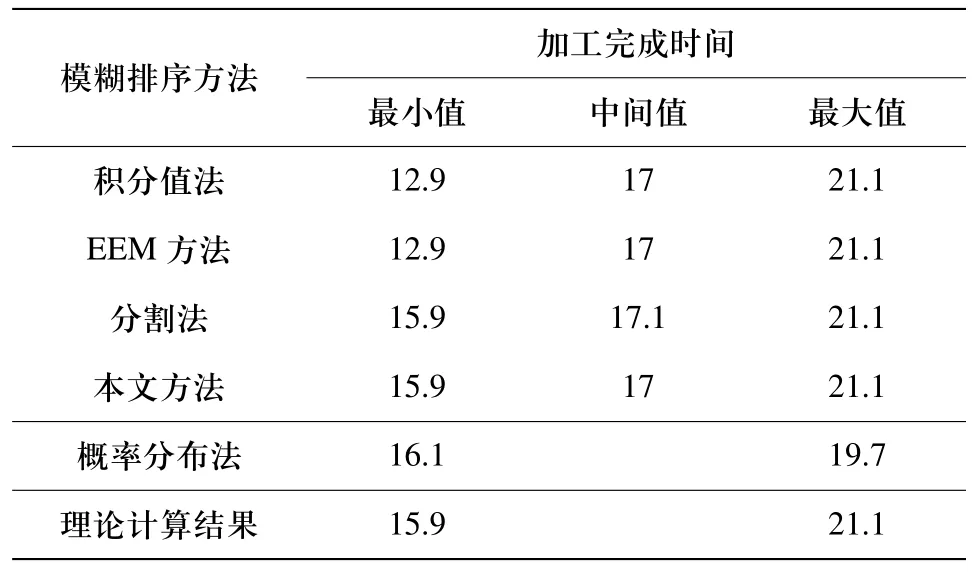
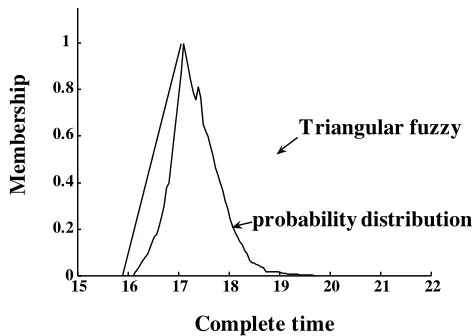
在排序过程中,并非所有的后续事件都要参与排序。因此需要从事件列表E中选取用于排序的模糊数集Fcomp。设事件E1,E2…Ei对应的模糊集为F1,F2…Fi,由模糊集的定义知,若sup(Fi) 图2 选取可比模糊数集合 令当前事件Ek对应的模糊集为Fk,t=sup(Fk),从事件列表中选取Fi={Fj│EEMFj(t)<1},令c=min(sup(Fi)), 则当inf(Fi)<c 时有Fi∈Fcomp,其中Fcomp为将要进行排序的模糊数集合。如图2中,由于inf(F5)>sup(F1),因此F5Fcomp,Fcomp=(F1,F2, F3, F4)。 当前事件结束时,需要从模糊数集Fcomp中选择下一个将要发生的事件。本文采用两个独立的参数来确定下一个要发生的事件,第一个为前一个事件的结束时刻Tnow,Tnow为一模糊数,其确定下一个事件将要发生的时间范围。设F1, F2, …Fk∈Fcomp,ai=inf(Fi),ci=sup(Fi),由上节中对Fcomp的选取可知,Tnow<min(sup(Fi)),因此对下一个事件的选取取决于当前时刻Tnow所处的位置。在Fcomp中,有inf(F1)< inf(F2)<…< inf(Fk),令Ii=[inf(Fi),inf(Fi+1)](1 ≤ i< k),Ik=[inf(Fk),sup(F1)], 如图3所示,Ii(1≤i≤k)将[inf(F1),min(sup(Fi))]之间分隔成k个区间。出于方便,设Ii=[ai,ci],mamum=min(sup(Fi)),则: 1)当Tnow<inf(F1)时,令S0=0 2)当Tnow∈Ii时,令 S0=0 设当前时刻为Tnow,有Tnow<inf(F1)或Tnow∈Ii,任取第二个参数λ∈[0,1],在区域Ii若λ∈[Sj-1, Sj],则取Ei作为下一个发生的事件。如图3中,Tnow∈I3,F3为选取的模糊数,其对应的事件E3将为第一个要发生的事件。 图3 模糊数排序示例 仿真开始时由用户指定好参数λ的值,该值在仿真过程中保持不变,由此再现系统的一个演化过程。排序过程中,一旦确定了下一个要仿真的事件,则需要对模糊数集Fcomp中各个模糊数的支集进行调整。如图4 ,若指定λ排序后有F1<F2,则仿真时钟将更新到F1,由于仿真时钟是一维的递增变量,因此模糊集F1的上界应该小于模糊集F2的上界。 设F1,F2,…Fk∈Fcomp,相应的隶属度函数分别为 μ1(x), μ2(x),…μk(x),Fp=min(F1, F2, …Fk)则 Fp为经排序后选定的下一个将要发生事件对应的模糊数。设 α=inf(x │ μp(x)>0),β=min(supSj│ j=1,2,…,k),则模糊集Fi按如下公式调整其隶属度函数: 其中 通过对仿真事件发生时间相应隶属度函数的调整,避免系统在仿真演化的过程中陷入一些不可能再现的状态中。 图4 模糊区间更新 下面将本文所述方法应用于一个生产加工系统[8],并将其结果与基于概率分布的方法和其他文献中基于模糊仿真的方法所获结果进行比较分析。设有生产系统S,系统中只有一台机器且只加工一类零件,加工时间及工件进入系统的时间为非确定的值,选取工件加工完成时间作为衡量系统性能的指标。测试数据如表1所示。 表1 工件到达时间与加工时间 仿真过程中,基于概率分布的方法采用与三角形模糊数相对应的三角形分布来处理不确定性。其中,第i+1个工件加工完成时间的概率分布等于前一个工件加工完成时间的概率分布与加工时间概率分布的卷积,因此利用卷积理论,可以由第一个工件逐步推导出最后一个工件加工完成时间的概率分布。以加工完成时间为衡量指标,各种方法下加工4个工件的仿真结果如表2所示。 由表2可知,理论上第4个工件的加工完成时间处于区间[15.9, 21.1]中,基于积分值和EEM的模糊排序方法工件加工完成时间均为三角形模糊数[12.9, 17, 21.1],由于这两种方法最小值小于15.9,因此仿真的结果有可能处于理论上不可达的状态中。这违反了前文所讲的模糊仿真应该满足的第二个属性。虽然分割法和本文提出的方法仿真结果符合理论值,对于分割法,当参数γ确定后,则对应的下一个要发生的事件是唯一的,如图5所示,当γ=γ0时,取F2。实际上,对于任意 的 γ, 使t=EEM-1M(γ)∈ [a2, c1], 有 F1<F2或F1>F2。因此基于分割法的模糊仿真在某些情形下不能演化系统中的所有可能出现的状态,而本文的方法可以再现系统中的所有状态。 表2 仿真结果 图5 分割法示例 基于模糊排序的仿真方法描述系统事件的演化时,系统输出参数是非确定性的模糊数。而对于基于概率分布的仿真方法来说,输出结果表示成以一定概率表示的统计分布。为了分析和比较这两种方法的输出结果,对概率分布进行正规化处理,将每一个输出结果的概率分布值除以最大的输出概率值。经过正规化处理后的概率分布与其模糊仿真结果如图6所示。 图6 工件加工完成时间 考虑到每次仿真结果的随机性,采用概率方法时需要对系统进行多次的仿真,仿真的次数将会影响输出参数结果,而且对于该方法来说,采用不同的分布函数和参数表达系统的不确定性,其输出结果也会存在一定的差别。由图6可知,基于概率分布仿真方法的输出结果包含于基于模糊数描述的输出结果中。因此,基于模糊数的仿真方法比基于概率分布的方法能够更好的表达系统演化过程的不确定性。 具有模糊参数的仿真可以表达系统的不确定性。针对离散事件系统中事件发生时间的不确定性,本文提出了一种新的模糊离散事件仿真方法, 该方法根据前一个事件结束时的当前时刻与其另一个待定参数确定下一个将要发生的事件。实验结果表明,与过去文献所提的方法相比,该方法能够满足离散事件仿真中的两个属性,同时,相对于基于概率分布的仿真方法,基于模糊的仿真方法能够更好的表达系统的不确定性。后续的工作主要研究不同的模糊数表示下仿真结果的关系与其分析不同分布函数和参数下基于概率分布的仿真方法和采用不同的参数下基于模糊集的仿真方法之间的定量关系。 [1] FISHMAN G S. Principles of Discrete Event Simulation[M].New York, John Wiley & Sons, 1978. [2] RIYADHR M, ABDULAZIZ A, HAKIM K. New fuzzy ranking algorithm for discrete event simulation[C]. // 12th IEEE International Conference on Electronics, Circuits and Systems, Gammarth, Tunisia, ICECS 2005. [3] LIOU T, WANG MAO JIUN. Ranking fuzzy numbers with integral value[J]. Fuzzy Sets and Systems, 1992,50(3): 247-252. [4] NGUYEN Q, LE T. A Fuzzy Discrete-Event Simulation Model[C].// Australia-Pacific Forum on Intelligent Processing and Manufacturing of Materials, Golds Coast, Queenland,Australia, July. 1997: 125-134. [5] ANGLANI A, GRIECO A, NUCCI F, et al. Representation and use of uncertainty in discrete event simulation models[C].[S.1.]: [S.n.], 1998: 717-731. [6] ZHANG Hong, TAM C.M, LI Heng. Modeling uncertain activity duration by fuzzy number and discrete-event simulation[J]. European Journal of Operational Research,2005, 164(4): 715-729. [7] 魏世豪. 具有模糊参数的离散事件系统仿真与输出分析研究[D]. 北京: 清华大学, 2008. [8] GRIECO A, NUCCI F, ANGLANI A. Representation of fuzzy time variable in discrete event simulation[J]. Integrated Computer-aided Engineering, 2003, 10(4): 305-318.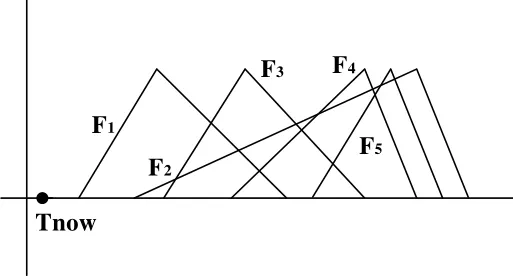
2.2 模糊事件选取
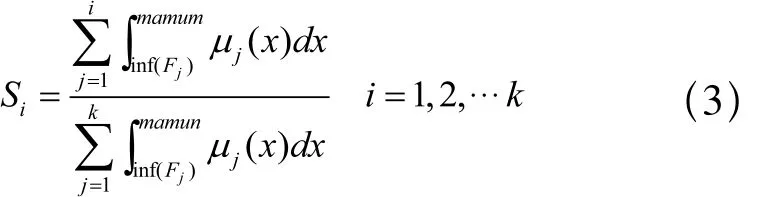
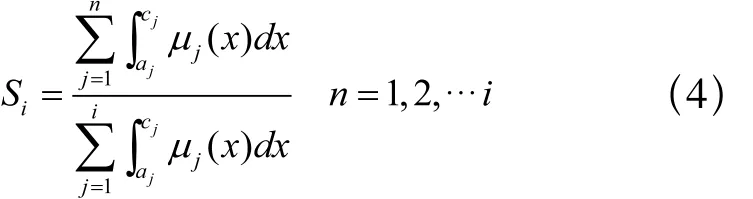
2.3 隶属度函数更新
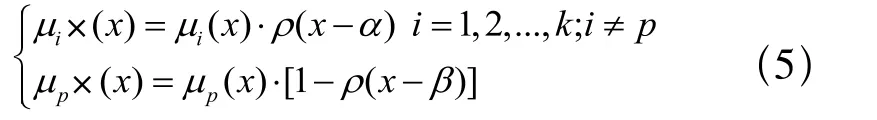
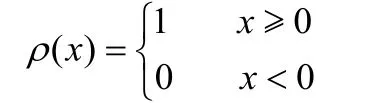

3 实验及结果分析
4 结论

