准晶材料中螺型位错与圆形夹杂的干涉效应

胡亚群，李建华

（湖南工程学院 机械工程学院，湘潭411101）

0 引 言

准晶材料的发现引起了晶体材料科学和数学上的巨大变革.大量的理论及实验表明具有复合结构和独特材料常数的准晶材料是有广阔前景的新型材料[1－3].准晶材料的力学性能显著的受到各种缺陷（如位错、裂纹、孔洞和夹杂等）的影响.近年来准晶材料中的缺陷问题吸引了大量学者关注的目光.Wang[4]研究了一维准晶的点阵及弹性行为.Peng和Fan[5]研究了一维准晶中的裂纹问题.Edagawa[6]回顾了准晶中线位错的典型特征.Li和 Fan[7]利用保角变换方法得到了一维六方准晶中位错与两条共线半无限裂纹的干涉解答.Liu和Guo[8]研究了一维六方准晶的平面弹性问题.

众所周知，材料生产和加工过程中有意加入或无意产生的夹杂都会显著的影响材料的性能.在复合材料力学性能的研究中位错与夹杂的干涉效应扮演着极为重要的角色.Dundurs和Mura[9]研究了刃型位错与圆形夹杂的干涉效应.Smith[10]considered考虑了位错与圆形夹杂的干涉问题并扩展了他的理论来处理纵向剪切下位错与椭圆孔或刚性椭圆夹杂的干涉问题.Luo和Chen[11]研究了刃型位错和圆形涂层夹杂的干涉效应.Xiao和Chen[12]研究了存在界面层时位错与圆形夹杂的干涉效应.但是，以上文献涉及的材料均为晶体材料，而准晶材料中位错与夹杂的干涉尚未有文献报道.

本文研究了一维六方准晶材料中螺型位错与圆形夹杂的干涉效应.利用复变函数方法，得到了由复势函数表示的边界条件以及应力场和位错力的解析表达式.并详细讨论了位错位置和材料差异对位错力及平衡位置的影响.

1 问题描述与一般处理

假设一维准晶原子沿z轴准周期排列而在xy平面内周期排列.如果位错线平行于一维准晶材料的准周期轴，那么材料的几何属性将不随准周期方向变化.令准晶材料的准周期轴为z轴，可得[3]

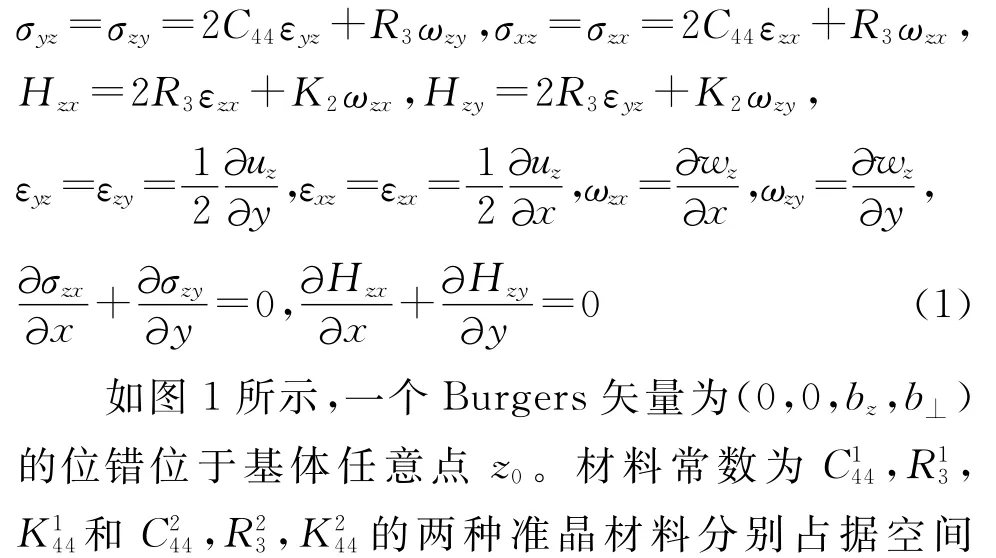
S＋和S－。两种材料界面为理想界面，下标‘1’和‘2’分别表示S＋和S－中的量.

图1 一维准晶材料中一个螺型位错位于圆形夹杂附近

此问题的控制方程为

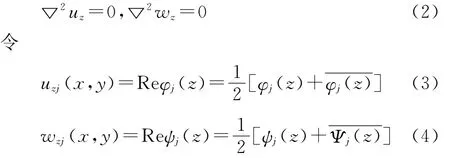
应力σxzj，σyzj，Hxzj，Hyzj及面力Tj，Mj可由解析函数φj（z），ψj（z）表示如下

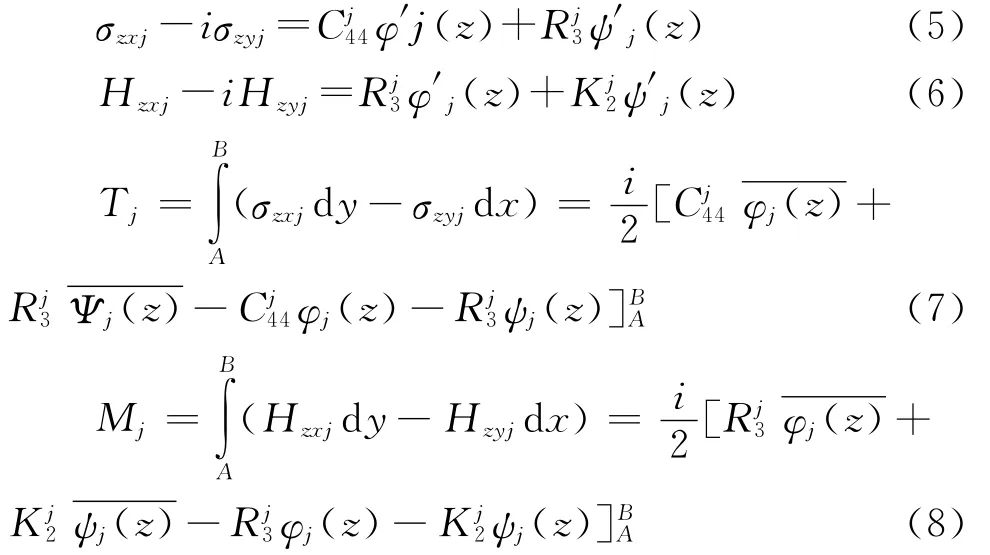
理想界面假设意味着界面上应力和位移保持连续，因此边界条件可表示为

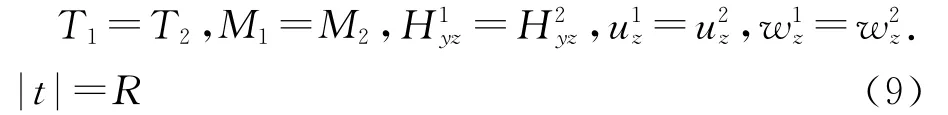
将式（5）～（8）代入式（9），边界条件可重新表示为

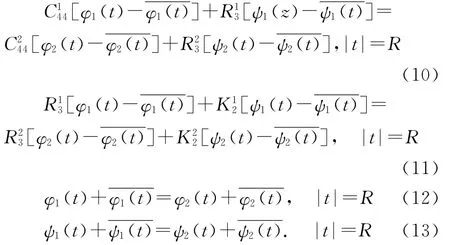
2 问题解答

根据文献[8]，均匀一维准晶材料中位于坐标原点的螺型位错产生的应力场为

将式（14）和（15）代入式（5）和（6）可得

如果一个burgers矢量为（0，0，bz，b⊥）的位错位于基体中任意点z0，则S－中的复势函数可表示为

其中φ20（z），ψ20（z），在S－中全纯．

为方便分析，根据Schwarz对称原理引入以下解析函数

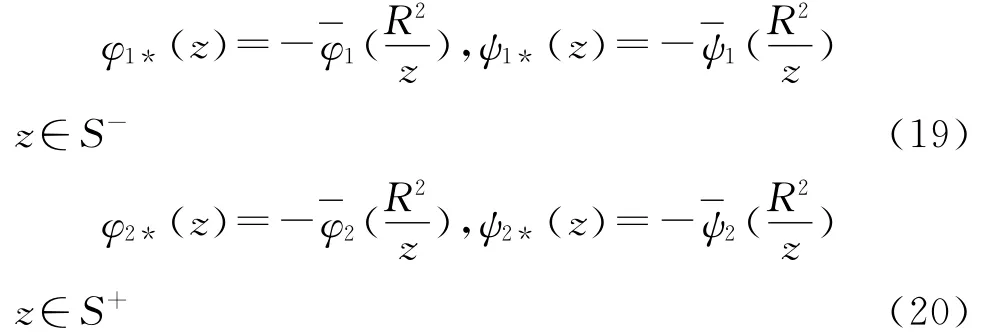
将式（19）和（20）代入式（10）～（13），边界条件可表示为

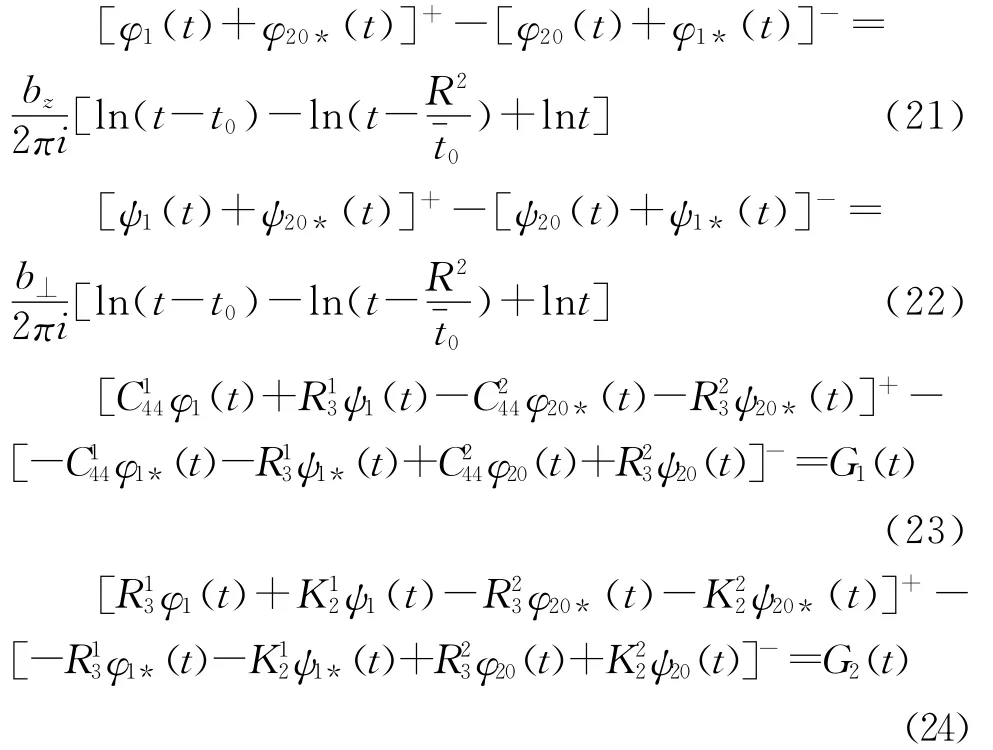
其中φ1（t）和φ1＊（t）全纯

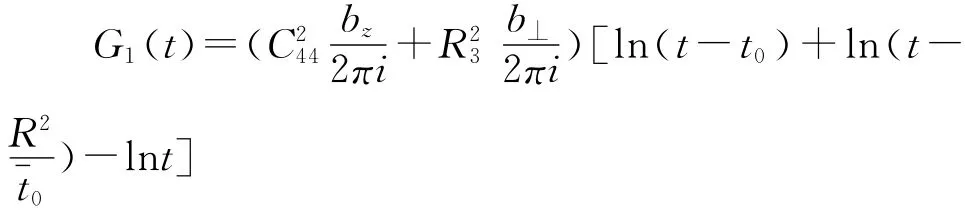
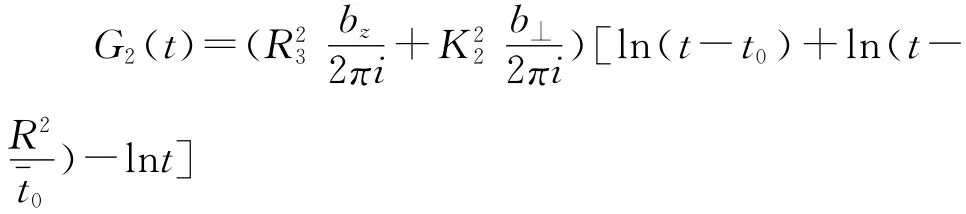
求解由式（21）～（24）表示的边值问题，并忽略表示刚体位移的常数，可得

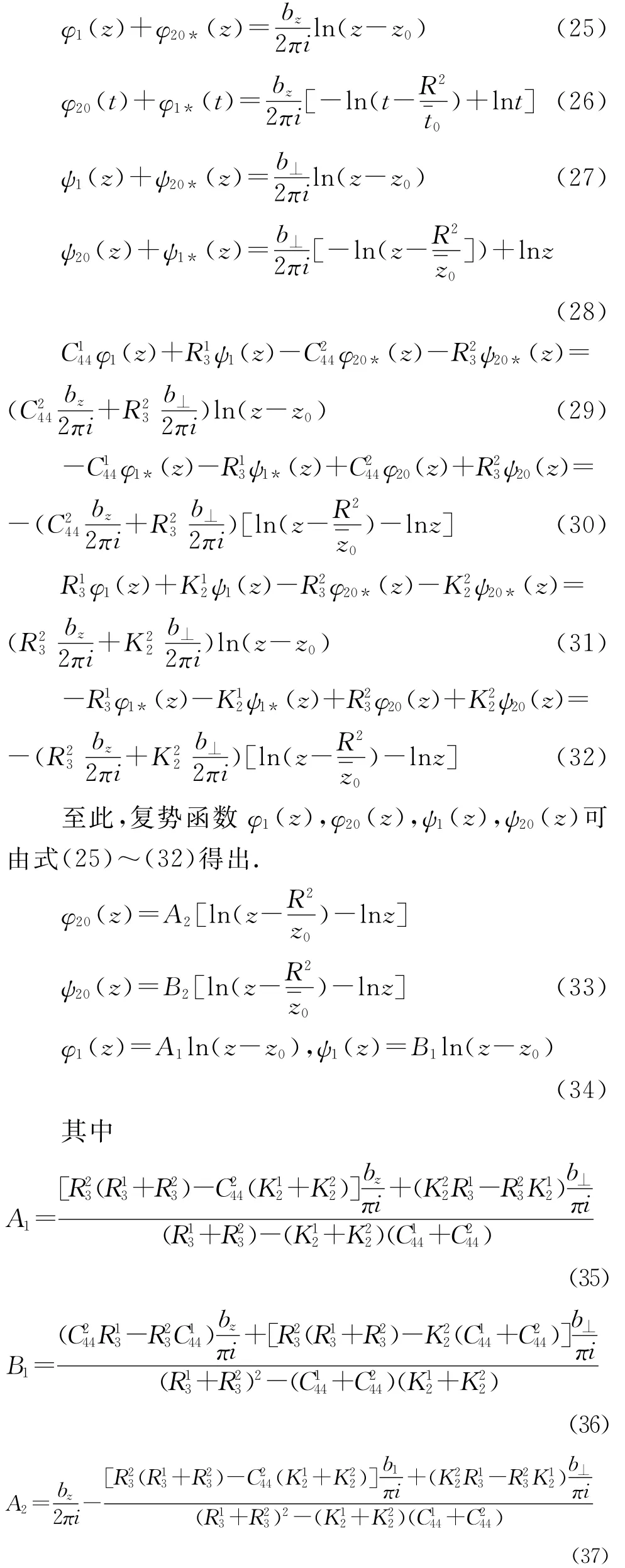
3 位错力

研究位错和夹杂相互作用时，描述相互作用机理的物理量为作用于螺型位错的像力，即位错力.位错力是理解位错和夹杂相互作用机制的重要物理量.对于一维准晶材料中的位错，根据推广的Peach－Keohler公式，位错力可表示为

4 讨 论

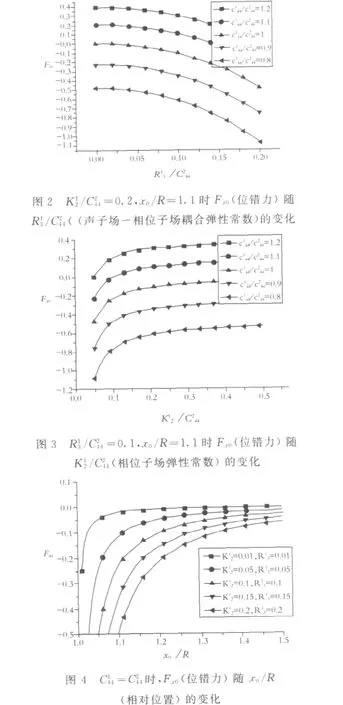
式（41）可退化为各种特殊实例，在此仅讨论最常见的情况，即晶体材料中镶嵌一个圆柱形准晶夹杂.这种情况（41）退化为

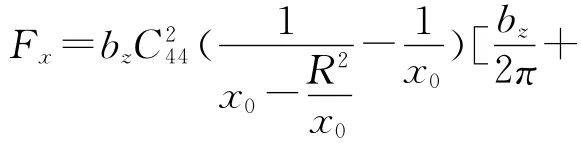
5 结 论

利用复变函数方法解决了一维准晶材料中位错与圆形夹杂的干涉问题.得出了由复势函数表示的边界条件，并得到了复势函数和位错力的解析表达式.算例表明特定材料参数下准晶夹杂附近存在位错的平衡位置，相位子场弹性常数和声子场－相位子场耦合弹性常数均存在可以改变位错力方向的临界值.

[1]Ronchetti M，Quasicrystals－an Introduction Overview[J].Philos.Mag，1987（56）：237－249.

[2]Hu C.Z.，Yang W.G.，Wang R.H.，et al.Quasicrystal Symmetry and Physical Properties[J].Prog.Phys.，1997（17）：345－375.

[3]范天佑.The Mathematical Theory of Elaiticity of Quasicrystals and Its Applications[J].北京工业大学学报，1999.

[4]Wang R.H.，Yang W.G.，Hu C.Z.，et al，Point and Space Groups and Elastic Behavious of One Dimensional Quasicrystals[J].J.Phys：Condensed Matter.1997，（9）：2411－2422.

[5]Peng Y.Z.Fan T.Y..Crack and Indentation Problems for One Dimensional Hexagonal Quasicrystal[J].Euro Phys Jour B，2001（21）：39－44.

[6]Edagawa K..Dislocations in Quasicrystals[J].Mater.Sci.Eng.，A 2001，309－310：528－538.

[7]Lian H.L.Fan T.Y..Exact Solutions of Two Semiinfinite Collinear Cracks in a Strip of One Dimensional Hexagonal Quasicrystal[J].Applied Mathematics and Comutation，2007.

[8]Liu G.T.，Gou R.P.，Fan T.Y..Plane Elasticity and Dislocation of One－dimensional Hexagonal Quasicrystal with Point Group[J].Journal of Beijing Institute of Technology，2005（14）：87－91.

[9]Dundurs J.and Mura T.，Interaction Between an Edge Dislocation and a Circular Inclusion[J].J.Mech.Phys.，Solids.1964，（12）：177－189.

[10]Smith E.，The Interaction Between Dislocations and Inhomogeneities－I[J].Int.J.Eng.Sci.，1968（6）：129－143.

[11]Luo H.A and Chen Y.，An Edge Dislocation in a Three－phase Composite Cylinder[J].Appl Mech.1991（58）：75－86.

[12]Xiao Z.M.，Chen B.J.，A Screw Dislocation Interacting with a Coated Fiber Mech[J].Mater.，2000（32）：485－494.