无速度传感器矢量控制系统转速辨识方法研究

林国汉，李晓秀

（湖南工程学院 电气信息学院，湘潭411101）

0 引 言

高性能交流传动系统要求对电动机进行速度闭环控制，必须实时获取电机速度反馈信号，这样就必须安装光电编码器或者测速发电机等高精度的速度和位置传感器，但传感器的存在会带来如维护困难、系统的机械鲁棒性和可靠性降低、系统成本增加、在恶劣环境下传感器的精度容易受到干扰的影响，以致无法工作等问题.因此，众多学者转为研究无速度传感器的交流传动系统，提出了许多无速度传感器矢量控制系统的速度辨识方法，主要有两类：基于理想电动机模型的转速辨识方法和基于非理想电动机模型的转速辨识方法.

1 转速辨识方法

近年来，对电机速度进行在线辨识一直是个热门课题，国内外学者针对无速度传感器技术进行了大量的研究工作，提出了许多算法，这些算法可以分成两类：第一类方法是基于电机理想模型的方法.这类方法利用电机的数学模型和检测到的定子电流、电压信号来估算电机的速度，如直接计算法（又可分为基于电压模型的转速辨识、基于电流模型的转速辨识、基于反电动势法的速度辨识）[1]、模型参考自适应法（MRAS）[2－3]、扩展卡尔曼滤波法（EKF）[4]、滑模观测器法（SMO）[5]、速度动态估算法（SDE）[6]、最小二乘法[7]、利用电机磁化电流无功功率实现转速辨识[8]、全阶闭环状态观测器法、PI自适应调节器法等.这类方法对电机模型进行了理想化的假设，依赖于电机的理想数学模型.第二类方法是基于非理想电机模型的方法.这类方法通过提取定子电流、电压谐波中包含的有关电机转子位置和速度信息来辨识电机的速度，如转子齿谐波法、高频信号注入法[9]、基于人工神经网络估计法[10]、基于模糊神经网络的速度辨识法[11]，基于鱼群算法的速度辨识[12]、基于遗传算法的速度辨识方法等[13－14]

无速度传感器技术已获得了广泛的应用，现将几种比较典型的转速辨识方法介绍如下：

1.1 基于理想电动机模型的转速辨识方法

1.1.1 速度动态估计器法

电机在对称运行的条件下，定子和转子的磁场为圆形旋转磁场并以同步角速度w1进行旋转，转子以w旋转，以转差ws切割旋转磁场，产生电磁转矩.通过磁通观测器，可以观测到转子磁通，由转子磁通可以得到同步转速，而由定子dq轴电流又可以得到转差速度，从而得到转子的旋转速度，即：

根据转子磁通ψra、ψrβ的变化就可以得到转子磁通旋转角：

在磁场定向的矢量控制系统中，将转子磁场定向于以同步速度旋转的dq轴的d轴上，即ψrd＝ψ2，ψrq＝0，转差角速度可由下式求得：

这种方法的优点是直观性强，理论上讲速度的计算没有延时.但是有如下缺点：由于缺少误差校正环节，难以保证系统的抗干扰性能，甚至可能出现不稳定的情况；需要知道磁通，因而受磁通观测与控制精度的影响；电机参数发生变化时，转速辨识精度会受到影响[1][4].

1.1.2 模型参考自适应法

模型参考自适应（MARS）法是一种常用的估算转子位置和速度的方法.其主要思想是将不含未知参数的方程作为参考模型，而将含有待辨识参数的方程作为可调模型，两个模型具有相同物理意义的输出量，利用两个模型输出量的误差构成合适的自适应律来实时调节可调模型的参数，以达到控制对象的输出跟踪参考模型的目的.这方面较有影响的是Shcuader提出的方法.

（3）提倡女性参加政治。秋瑾有较强的政治意识，提出妇女应当关心时政，拥有爱国思想。因为如果国亡，权利亦亡。保国，就是保权利。应把权利与义务联系起来，把女子尽义务，参与革命，作为争取女性权益的条件之一。岸田俊子首次以国家观念为媒介而开始参与政治活动，在这种国家观念中，最为显著的就是强烈的“爱国之情”。不仅如此，岸田还将矛头指向男性民权家，期待将女性解放伸张纳入到男性民权家的话语中去，以图谋求女权。

通过异步电动机在两相静止坐标系下的电压电流方程，可以得到转子磁链观测器的两种不同模型.

电压模型：

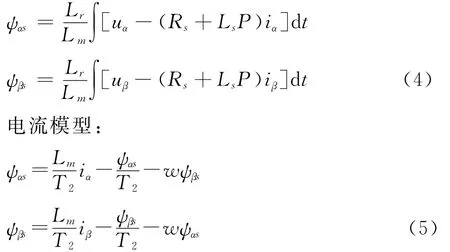
从式（4）、式（5）可知，电压模型不含待辨识转速w，作为参考模型，而含有待辨识转速 的磁链方程（电流模型）作为可调模型，利用电压模型的输出作为转子磁链的期望值，电流模型的输出作为转子磁链的推算值，以转子磁链 和 作为比较输出量，采用PI自适应律估计转速＾w ，自适应机构的采用波波夫的超稳定性理论来进行设计，以保证状态收敛[8].其原理框图如图1所示.

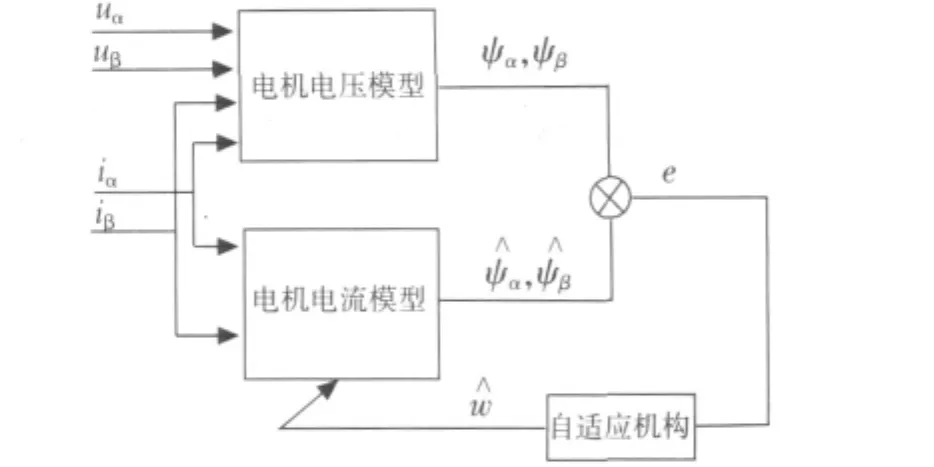
图1 模型参考自适应速度辨识框图

MRAS在异步电机及永磁同步电机的无速度传感器控制中已有很多应用.但是这种方法基于电机的基波模型，当电机参数发生变化时，转速的估计精度将下降，尤其在电机低速运行时更为严重.由于MRAS的速度观测是以参考模型的准确为基础的，参考模型里包含的电机参数准确程度将影响到速度辨识和控制效果，所以需要考虑对多个参数同时进行辨识，并保证参数和系统状态同时收敛到真值[14－15].

1.1.3 滑模观测器法

滑模控制的基本想法是定义一个切换面S（也叫滑动参数），保证在这个切换面上系统是稳定或至少是近似稳定的，然后用控制信号把系统调整到这个切换面上.即用一种控制的方法，使s和系统误差e在有限时间内收敛到零.为确保电流观测器的收敛性，就产生了等效控制（找一种等效控制，强迫系统运行在滑模面上，即在这种控制下系统的运动正好就是滑模面上滑动模态的运动）.对于滑模面上的运动，应满足s（X）＝0，sg（X），然后将等效控制用于磁通观测来产生 轴和 轴磁通，继而使用观测到的磁通来估算电机转速.根据在转子磁场定向的两相静止α－β坐标系下，以定子电流和转子磁通为状态变量的异步电动机模型，设计以下的观测器[5]：

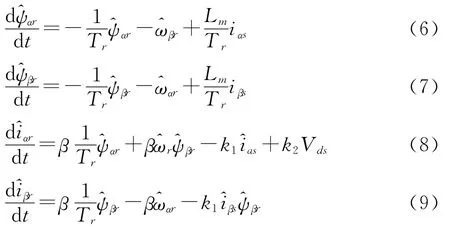
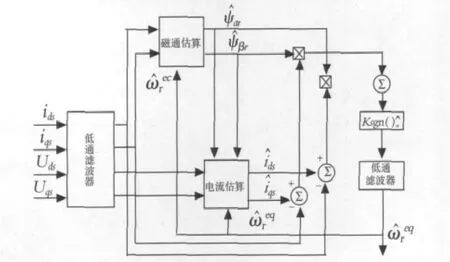
图2 滑模观测器速度辨识框图

1.1.4 扩展卡尔曼滤波器法

卡尔曼滤波是上世纪发展起来的一种滤波方法，它的突出特点是可有效削弱随机干扰和测量噪声的影响.当噪声是正态分布时，卡尔曼滤波给出状态的最小方差估计，当不是正态分布的噪声时，则给出状态的线性最小方差估计.一般情况下，卡尔曼滤波用于线性系统的状态估计，如果用于估计象异步电动机这样的非线性系统的状态时，则必须考虑使用扩展卡尔曼滤波.扩展卡尔曼滤波器（EKF）是线性卡尔曼滤波器在非线性系统中的推广应用.它将电机转速看作状态变量，并把电机模型增广为五阶非线性模型，在每一步估计时将时域下的电动机模型在运行点进行线性化，再沿用线性卡尔曼滤波器的递推公式进行估计，这种方法可有效地抑制噪声，提高转速估计的精确度.但EKF的计算量大，即使采用降阶的卡尔曼滤波器也是如此，而且在滤波前误差和测量噪声的统计特性必须已知.同时，在对参数的鲁棒性上仍显得无能为力，尤其是低速时很难取得较满意的结果.为满足实时控制的要求，需要用高速、高精度的数字信号处理器来完成计算，这使得无速度传感器变频调速系统的硬件成本提高.

1.2 基于非理想电机特性的转速辨识方法

1.2.1 转子齿谐波法

基于理想电动机模型的转速辨识方法都依赖于电动机模型，因此不可避免地受到电动机参数变化的影响.为克服速度辨识中对电机参数的依赖性，研究者提出了利用基于转子齿谐波信号中与转速相关的频率成分来提取转速的思想.转子齿谐波的转速估计不是从转速与电动机状态的关联中间接地获取转速，而是从转子齿谐波的物理信号中直接提取转速信息.由于电机定子表面和铁芯上的齿槽会在气隙磁场中产生齿谐波，在谐波作用下，电机的电压和电流信号会产生相应的谐波，这种谐波的频率与转速是相关的，因此，可以从齿谐波信号中提取相关频率，根据频率与速度的关系来推算转速.而且电流谐波是由转子机械和电磁的不对称引起的，因此辨识不依赖于电机参数，即使在频率很低时也能可靠工作[1].

1.2.2 高频信号注入法

转子齿谐波法中所检测的谐波是在基波信号激励下形成的，由于在低速时该信号强度较弱，容易受到噪声干扰.美国的Lorenz等学者另辟蹊径，提出了高频信号注入法.其基本思想是在电机的定子侧注入高频电压或者电流信号，利用产生的高频效应来检测相关量，进而提取其中所包含的电机转速信息，达到辨识转速的目的.目前比较常用的高频信号注入法主要有转子凸极性法和dq轴阻抗差异法[9].

设高频信号电压为u1i，频率为wi，则在定子静止坐标系下的电压方程为：

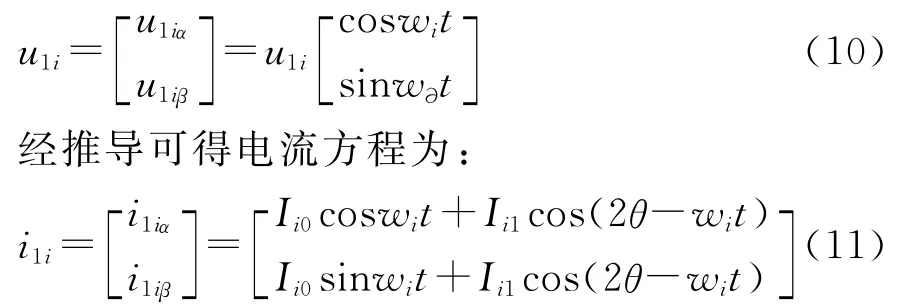
1.2.3 基于神经网络、仿生智能的速度辨识法

基于人工神经网络（ANN）的速度辨识是通过学习系统的输入输出量逐渐提高控制器的性能，达到所需的性能指标.因为该速度辨识方法不依赖于电动机参数，所以对电机参数变化和噪声具有鲁棒性.使用ANN辨识常见的方法是多层前馈ANN和基于MRAS的两层ANN网络.但前馈神经网络采用的是沿梯度下降算法，存在训练时间长，局部极小点等问题.近年来，人们一直在利用来自生物系统的灵感来解决实际问题，并构造和设计出许多仿生优化算法，如遗传算法、蚁群算法、微粒群算法、人工鱼群算法等，他们都属于模拟自然界生物系统行为或过程的最优化仿生智能算法，众多学者将神经网络与仿生智能算法相结合，并应用于无速度传感器矢量控制系统的速度辨识，取得了较好的辨识效果.提出的算法主要有：基于遗传算法的小波神经网络速度辨识、人工鱼群神经网络速度辨识、蚁群算法优化神经网络的速度辨识方法、基于粒子群算法的BP神经网络的速度辨识方法.

上式中高频激励产生的高频电流信号中含Ii0一项与转子位置无关，Ii1则与电机转子位置有关.因此可以设法去掉Ii0的干扰，只留下Ii1，然后进过滤波环节和控制，使得转子位置的推算值＾θ趋向于转子位置实际值θ，通过下式则可求得转子角速度：

2 仿真模型设计与试验

本文在采用矢量控制基础上，利用MATLAB／SIMULINK，建立了无速度传感器矢量控制系统仿真模型，对几种常用的转速辨识方法进行了仿真研究，其中所使用的异步电机参数为：额定功率PN＝2.5kW，频率f＝50Hz，额定转速nN＝1440r／min，定子电阻Rs＝1.85Ω，转子电阻Rr＝2.658Ω，定子电感Ls＝0.294H，转子电感Lr＝0.2898H，互感Lm＝0.2838H，极对数np＝2，转动惯量J＝0.01kg·m2.

仿真实验一：电机空载启动实验.电机给定转速为额定转速1440r／min，仿真结果如图3～图6所示.

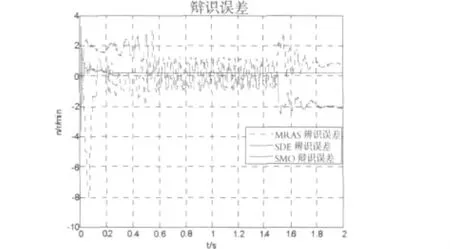
图6 空载时速度辨识误差曲线

仿真实验二：电机带变化负载启动实验.电机给定转速为额定转速1440r／min，在t＝0.8s时负载为10N·m，时间t＝1.3s时撤去负载.仿真曲线如图7～图10所示.

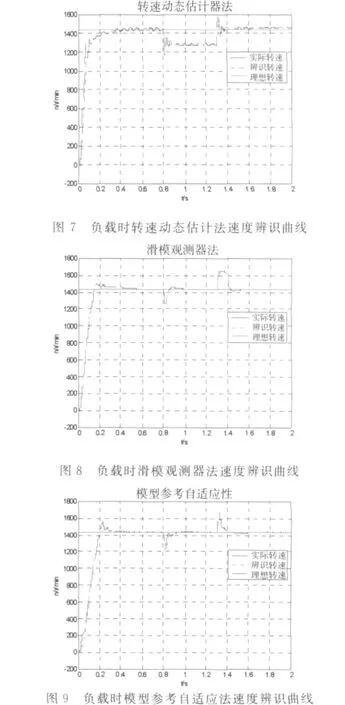
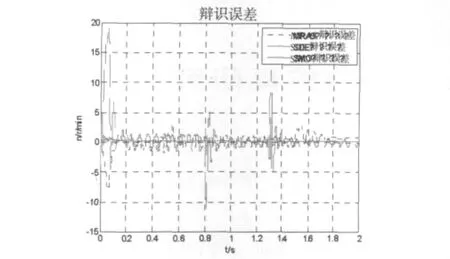
图1 0 负载时速度辨识误差曲线

从仿真实验波形中可以看出，不管是空载启动还是变负载启动，对于三种速度辨识方法，转速都能能迅速跟随给定变化，转速在转矩变化时会出现波动，动态速度估计器法的波动较大，经过一段时间波动后能跟随速度变化，表明电机有一定的负载能力.相对于其它两种方法，参滑模观测器法的辨识误差较小，但在负载变化瞬间，滑模观测器的辨识误差较其它两种方法大.

3 结束语

本文对无速度传感器速度辨识方法进行了仿真研究.各国学者在无速度传感器异步电机矢量控制系统方面已做了很深入的研究，未来一段时间内，主要研究热点包括：零频率问题及低频问题的处理、铁耗的影响、异步电机磁通的直接检测、电阻和转速的同时辨识等.

[1]冯垛生，曾南岳.无速度传感器矢量控制原理与实践[M].北京：机械工业出版社，2006.

[2]徐中领.基于D S P的交流异步电动机无传感器矢量控制系统的研究[D].南京：南京航空航天大学，2007.

[3]祝龙记，王 宾.基于 MRAS速度辨识矢量控制系统的仿真研究[J].电工技术学报，2005，20（1）：60－65.

[4]李剑飞，尹 泉，万淑芸.基于扩展卡尔曼滤波器的异步电机转速辨识[J].电工技术学报，2002，17（5）：40－44.

[5]李春菊，刘国荣，蔡斌军.基于滑模磁通和速度观测器的异步电动机间接磁场定向控制[J].湖南工程学院学报（自然科学版），2009，（4）：48－50.

[6]贾 涛，王耀南，黄守道，李新田.基于转速动态估计器的无速度传感器感应电机矢量控制系统研究[J].电气传动自动化，2004，26（4）：1－4.

[7]周俊勇，金 阳，南余荣，钟德刚.异步电动机速度辨识方法的研究[J].电气传动自动化，2004，26（2）：1－3.

[8]朱鹏程，陈 坚，康 勇.利用电机磁化电流无功功率实现转速的在线辨识[J].电气传动，2003，（5）：12－14.

[9]Schauder C.Adaptive Speed Identification for Vector Control of Induction Motors Drive[J].Proceedings of the IEEE，2002，90（8）：1359－1394.

[10]杨会东，李 岚.自适应神经网络在异步电动机转速辨识中的应用[J].微特电机，2007，（4）：43－45.

[11]彭望成.基于模糊神经网络的异步电机转速估计方法[J].电机与控制应用，2008，35（7）：5－9.

[12]曹承志，毛春雷.人工鱼群神经网络速度辨识器及应用[J].计算机仿真，2008，25（10）：291－294.

[13]张寅孩，严利平，张仲超.基于遗传算法辨识噪声模型的异步电机闭环卡尔曼速度估计[J].电机与控制学报，2005，2（9）：151－165.

[14]张敬恩.无速度传感器变频调速系统转速辨识方法研究[J].电工电气，2010，（2）：18－22.

[15]佘致廷，袁俊波，郑 勇等.交互式模型参考自适应PMSM 速度辨识[J].电气传动，2011，41（3）：3－7.