基于数值仿真和灰色关联分析法的高强钢弯曲回弹影响因素分析

谢延敏，王 智，胡 静，罗征志，彭 炼

(西南交通大学机械工程学院，成都 610031)

随着现代汽车工业的高速发展，为了减轻车重、节能减排、提高碰撞安全性，汽车用钢板向高强度化发展已成为必然趋势。另一方面，在板料成形领域，回弹一直是最为严重的缺陷之一。高强度钢的机械性能与普通低碳钢有很大差异，钢板高强度化易引起塑性下降，成形性变差。因而对于高强钢圆形冲压件，回弹是最主要也是最难控制的质量特性。要预防和减少高强钢成形的回弹，就必须对影响高强钢成形回弹的因素进行分析。影响成形件回弹量的因素很多，为了减少回弹，获得最佳工艺参数，需要对影响回弹量的因素进行深入研究［1－2］。

本文对NUMISHEET 2002中的高强钢圆形件进行无约束自由弯曲回弹仿真，证明利用 Dynaform软件能够准确地预测回弹。建立了高强钢圆形弯曲件的有限元仿真模型，并通过灰色关联度法分析了冲压速度、板料厚度、板料宽度、模具闭合高度、凹模圆角半径、凸模摩擦因数以及凹模摩擦系数这些工艺参数对高强钢圆形件回弹的影响程度，分析出了影响高强钢圆形件弯曲回弹的主要因素。

1 圆形件自由弯曲变形过程

研究对象采用的是圆形件自由弯曲的冲压加工，毛坯材料是高强度钢板，受力如图1所示［3］。

图1 圆形件自由弯曲过程

开始弯曲时，工件的支承点在A－A。随着凸模进入凹模深度的增大，凹模与板料的接触位置发生变化，支承点沿凹模不断内移，两支承点间距离由开始的2ω逐渐缩短，变形区弧长s=(ρ+t/2)θ也随之变化。分析可知，变形区范围s随弯曲变形而逐渐向中间缩小，非变形区就逐渐向中间扩大，但扩大的部分已不是未经变形的平直状态，而是已经发生过弯曲变形的状态，其曲率半径由中间的r向外逐渐增大，类似渐开线。

2 有限元软件模拟

2.1 有限元建模及验证

Dynaform软件是用于板料成形数值模拟的专用软件，可以预测成形过程中板料的裂纹、起皱、减薄、划痕、回弹、成形刚度、表面质量，评估板料的成形性能，从而为板成形工艺及模具设计提供帮助。

2.1.1 有限元仿真模型的建立

首先在UG中建立凸模、凹模和坯料的面模型。凸模和凹模的尺寸如图2所示，径向长度为50 mm。板料的长度为120 mm，宽度为30 mm，厚度为1 mm。然后将面模型导入Dynaform软件，对模型进行网格划分，得到仿真模型。单元类型选Full Integrated(全积分单元)，设置壳单元在板材厚度上的积分点为7，仿真模型见图3。

图2 凸模、凹模尺寸

图3 仿真模型

2.1.2 参数设置

高强钢的物性参数见表1。设置高强钢仿真实验的冲压速度为 2 000 mm/s，摩擦因数为0.148 17。

2.1.3 回弹角的定义

NUMISHEET 2002圆形件无约束自由弯曲回弹角的定义如图4所示。将弯曲件边缘AB和CD的夹角回弹前后的差值定义为回弹角。

图4 回弹角的定义

表1 高强钢的的物性参数

2.1.4 仿真结果与实验结果对比

高强钢模拟仿真的结果与实验结果对比见表2。

表2 仿真结果与实验结果对比

经过验证可知，用Dynaform软件模拟得出的回弹结果与实验值误差仅为2.91%。所以，利用Dynaform软件对高强钢成形过程进行模拟，得出的回弹值在误差范围之内，证明有限元模型是正确的。

2.2 圆形件自由弯曲回弹因素正交水平设计

在冲压工艺中，影响成形回弹的因素主要有板料厚度、板料宽度、冲压速度、模具闭合高度、凹模圆角半径、凸模摩擦因数以及凹模摩擦因数等。利用建立的有限元仿真模型，采用正交设计方法分析各影响因子对回弹的影响，获得减少回弹量的可控因子水平组合［4－5］。对于各影响因子水平选择所建立的正交表如表3所示。表中:A为板料厚度(mm);B为板料宽度(mm);C为冲压速度(mm/s);D为凹模圆角半径(mm);E为凸模摩擦因数;F为凹模摩擦因数;G为冲压行程(mm)。高强钢材料为DP500。

3 灰色关联度分析

灰色关联度分析的目的在于对信息不完全与“少数据不确定”的系统做因子间的量化、序化，明确在众多因素中，哪些是主要因素、哪些是次要因素，哪些对系统发展起推动作用、哪些对系统发展起抑制作用等。运用灰色关联度进行因素分析是非常有效的，而且特别适用于各个影响因素和回弹量之间不存在严格数学关系的情况。因此，采用灰色关联分析，可有效地计算出各因素对高强钢圆形件弯曲回弹的影响程度，筛选出影响高强钢圆形件弯曲回弹的主要因素［10－13］。

灰色关联度分析的核心是计算关联度。一般说来，关联度的计算首先要对原始数据进行处理，然后计算关联系数，由此就可计算出关联度［10］。

表3 各影响因子正交设计实验结果

3.1 原始数据的处理

由于各因素有不同的计量单位，因而原始数据存在量纲和数量级上的差异，不同的量纲和数量级不便于比较，或者比较时难以得出正确结论，因此，在计算关联度之前，通常要对原始数据进行无量纲化处理，方法包括初值化、均值化等。

本文采用均值化对原始数据进行处理。初值化处理，即用同一数列的第1个数据去除后面的所有数据，得到一个各个数据相对于第1个数据的倍数数列，即初值化数列。

3.2 计算关联系数

设经过数据处理后的参考数列(回弹量)为

与参考数列作关联程度比较的P个数列(常称为比较数列，即为各个影响因子)为

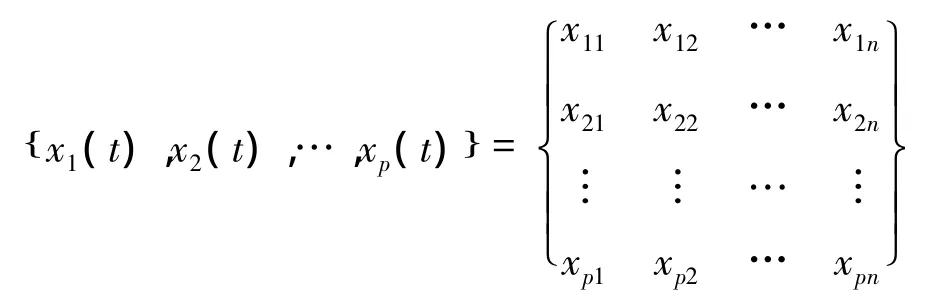
式中n为数列的数据长度，即数据的个数。从几何角度看，关联程度实质上是参考数列(回弹量)与比较数列(影响因子)曲线形状的相似程度。凡比较数列与参考数列的曲线形状接近，则两者间的关联度较大;反之，如果曲线形状相差较大，则两者间的关联度较小。因此，可用曲线间的差值大小作为关联度的衡量标准。

将第k个比较数列(k=1，2，…，p)各期的数值与参考数列对应期的差值的绝对值记为

对于第k个比较数列，分别记n个Δ0k(t)中的最小数和最大数为 Δ0k( m in )和Δ0k( m ax)。对P个比较数列，又记P个Δ0k( m in)中的最小者为Δ( m in)，P个 Δ0k( m ax)中的最大者为 Δ( m ax)。这样Δ( m in)和Δ( m ax)分别是所有P个比较数列在各期的绝对差值中的最小者和最大者。于是，第k个比较数列与参考数列在t时期的关联程度(常称为关联系数)可通过下式计算:

式中ρ为分辩系数，用来削弱Δ( m ax)过大而使关联系数失真的影响，人为引入这个系数是为了提高关联系数之间的差异显著性，0＜ρ＜1。

3.3 求关联度及排序

由于每个影响因子与回弹量的关联程度是通过n个关联系数来反映的。关联信息分散不便于从整体上进行比较，因此，有必要对关联信息作集中处理。而求平均值便是一种信息集中的方式，即用影响因子与回弹量各个时期的关联系数之平均值来定量反映两者的关联程度，计算公式为

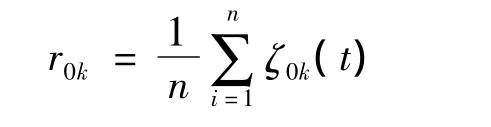
式中r0k为第k个影响因子与回弹量的关联度。

运用灰色关联分析，将上一步正交实验得到的数据结果带入，计算可得:r0k=({0.762 7 0.788 7 0.669 6 0.815 4 0.635 7 0.628 8 0.784 6}T，(k=1，2，…，7)。

各因素按照关联度大小进行排序r04＞r07＞r02＞r01＞r03＞r05＞r06，表明在高强钢圆形件自由弯曲回弹中，凹模圆角半径、冲压行程、板料宽度以及板料厚度是主要的影响因素，其中凹模圆角半径影响更大，而冲压速度、凸模摩擦因数以及凹模摩擦因数为间接影响因素，对回弹的影响较小。

4 结束语

1)本研究使用的板料成形仿真软件Dynaform建立的有限元模型可有效预测高强钢圆形件自由弯曲回弹。

2)由灰色关联分析可知:凹模圆角半径、冲压行程、板料宽度以及板料厚度为影响高强钢圆形件自由弯曲回弹的主要因素;而冲压速度、凸模摩擦因数以及凹模摩擦因数为影响较小的间接影响因素。

3)本文所采用的有限元数值模拟方法和灰色关联分析可以推广到同类型加工问题的仿真建模以及因素分析中。

［1］谷诤巍，徐勇，程万军.高强度钢板冷冲压成形数值模拟研究［J］.汽车工艺与材料，2010(1):68－70.

［2］谷瑞杰，杨合，詹梅，等.弯曲成形回弹研究进展［J］.机械科学与技术，2005，24(6):653 －658.

［3］Durairaj VASUDEVAN，Rajumani SRINIVASAN，Palani PADMANABHAN.Effect of process parameters on springback behaviour during Vasudevan et al［J］.Zhejiang Univ-Sci A(Appl Phys ＆ Eng)，2011，12(3):183－189.

［4］Li G Y，Tan M J，Liew K M.Prediction of springback by using explicit finite element method in conjunction with orthogonal regression analysis［J］.International Journal of Solids and Structures，1999，36(2):4653 －4668.

［5］潘尔顺，徐小芸.基于有限元法与田口法的V形件冲压仿真参数稳健设计［J］.上海交通大学学报，2005，39(7):1077－1081.

［6］Saurav Datta，Asish Bandyopadhyay，Pradip Kumar Pal.Grey-based taguchi method for optimization［J］.Int J Adv Manuf Technol，2008，39:1136 －1143.

［7］Tsao C C.Grey-Taguchi method to optimize the milling parameters［J］.Int J Adv Manuf Technol，2009，40:41–48.

［8］孙芳芳.浅议灰色关联度分析方法及其应用［J］.科技信息，2010(17):880－882.

［9］罗佑新，张龙庭，李敏.灰色系统理论及其在机械工程中的应用［M］.长沙:国防科技大学出版社，2001.

［10］谢延敏，于沪平，陈军，等.基于灰色系统理论的方盒件拉深稳健设计［J］.机械工程学报，2007，43(3):54－59.

［11］王军延，张远新，王宝和.基于灰色模型的某型装备可靠性相关参数预估［J］.四川兵工学报，2011(2):8－11.

［12］曾小红，毕海普，甘元庆.灰色理论在我国化工园区事故预测中的应用［J］.重庆工商大学学报:自然科学版，2011(2):186－190.

［13］邹程林，苏维词，唐为亮，等.重庆工业专门化部门与经济增长的灰色关联分［J］.重庆师范大学学报:自然科学版，2009(4):62 －66.