应用电容层析成像对气固颗粒浓度分布的研究
王泽璞,刘 乾,曹丽平,刘 言,刘 石
(华北电力大学能源与动力工程学院,北京 102206)
高密度循环流化床(HDCFB)具有高效传热传质,可输送气固两相流,因而被广泛应用于各个工业领域,比如燃烧检测、催化裂解和合成等。气固两相流的流动充满不确定性、复杂性,伴随有流动的集群和非均匀流动等特性[1-2]。气固两相流中的固相介质分布特征对床内传热传质、高效环保工作具有重要作用。目前,测量HDCFB中气固两相流固相介质分布的方法有电容法、差压法、静电方法、光学法、χ射线法、γ射线法、超声波法、核磁共振法和电磁共振法等。由于被测对象的封闭性和复杂性,上述方法都不能精确测量HDCFB内固相介质的分布特性。
近年来,逐渐被关注的过程层析成像技术(PT)是一项具有非侵入性特性的在线检测技术。可通过PT技术直接检测流动设备内的流动特性,以优化设备系统的设计及提高设备的运行效率。PT技术能成功应用的关键因素是有特定的传感器系统和合适的图像重建算法。其中,电容层析成像技术(ECT)由于其成本低,采集速度快,在多相流流动检测和多孔介质火焰可视化方面得到成功应用。本文选用ECT技术在线检测高密度循环流化床(HDCFB)内流动的固相介质截面分布及流动模型识别。ECT技术在线检测流型识别的关键在于选取合适的图像重建算法。已开发的ECT图像重建算法大致分为2类:静态图像重建算法和动态图像重建算法。已被成功应用的ECT静态图像重建算法有线性反投影法(LBP)[3]、Tikhonov正则化方法[4]、Landweber迭代算法[5-7]、离线迭代和在线重建(OIOR)算法[8]、截断奇异值分解(TSVD)算法[9]、遗传算法[10]、采样广义矢量模式匹配法[11]、广义 Tikhonov 正则化方法[12-14]、模拟退火算法[15]、神经网络算法[16-17]、水平集方法[18-19]、代数重建技术(ART)和同时迭代重建技术(SIRT)算法[9]。这些静态图像重建算法在ECT发展过程中发挥着非常重要的作用。然而这些算法在重构过程中只考虑ECT测量信息,重建图像质量欠佳。为了增加ECT图像重建过程的信息量,显著提高图像的重建质量,本文提出了同时考虑流动管道内被测对象的空间约束、时间约束和流动物理演化信息的广义动态图像重建算法。
1 动态图像重建算法
基于被测电容值,ECT技术凭借相应的重建算法重构被测对象的截面介电常数分布。一般ECT图像重建过程包括正问题和反问题2个方面。ECT正问题是指已知流动管道截面上各相介质的介电常数分布,求解ECT传感器各电极对间的电容值。而ECT反问题是指依据被测电容数值反演流动管道内各相介质的分布特性。ECT技术在工业上的检测应用问题属于ECT反问题。
实际应用中,ECT图像重建模型可简化为

式中:C是一个m×1维向量,表示归一化电容值;G是一个n×1维向量,表示归一化介电常数分布值,代表重建图像的灰度值分布;S是一个m×n矩阵;r是一个m×1维向量,表示测量噪音信息。
方程(1)是静态图像重建算法的本质,其重构过程只运用ECT的采集测量信息,忽略了循环流化床内两相流介质的流动特性。因此,本文提出一种集合ECT测量信息和管道内介质流动特性的广义动态图像重建算法,其动态图像重建模型可表示为:
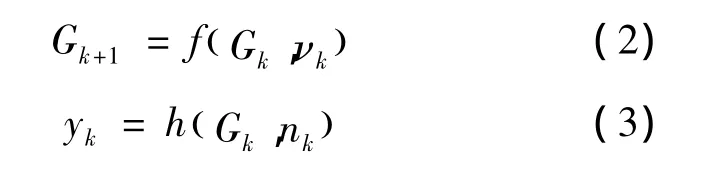
式中:Gk是k时刻的未知量;f(·)描述管道内介质的流动特性,可用一组多相流测量的偏微分方程组表示;h(·)是测量方程;yk表示k时刻测量的电容数据;νk代表介质流动过程的不确定性,这是由于理论模型的简化突显其在实际应用中的重要性,并且很难获取实际过程的初始条件和边界条件;nk用来描述实际测量过程中的不确定性。在ECT实际应用中,可把方程(2)和(3)线性简化为

式中:Fk表示k时刻的演化算子;Hk表示测量算子,在ECT图像重建过程被称为敏感场矩阵。假设Fk=I,I是单位矩阵,则方程(5)可看作纯随机性演变模型,此模型经常被应用于无法确定更好的时空模型的情况。理想情况下,非线性动态模型可被融合到静态转换算子Fk中。
2 实验装置
实验的高密度循环流化床(HDCFB)系统包括有鼓风机系统、通风系统、物料循环系统和空气压缩系统。ECT安装在提升管道部分,管道直径0.23 m、高9.8 m。实验循环输送砂土,其密度为2 432 kg/m3,平 均 粒 度 为 268 μm,堆 积 密 度为1 860 kg/m3。
3 实验结果分析
在实际工业应用中,获取HDCFB中横截面各相介质的分布信息非常重要。基于ECT在线检测技术信息,验证提出的广义动态重建算法的精确性,并且与小波多尺度分析方法计算得到的横截面各相介质浓度分布作比较。
1)空气流速11 m/s。在实际操作中,HDCFB中横截面固相介质的分布很大程度上受空气流动率的影响。本实验ECT检测过程中实际的空气流速为11 m/s。图1显示了ECT在线检测的HDCFB中横截面各相介质的分布。图2展现了某一检测周期内管道横截面的固相介质的体积分布。先用“Daubechies4”小波分析法多尺度分析固相介质的体积分数变化波动趋势,其最大解析度为3。
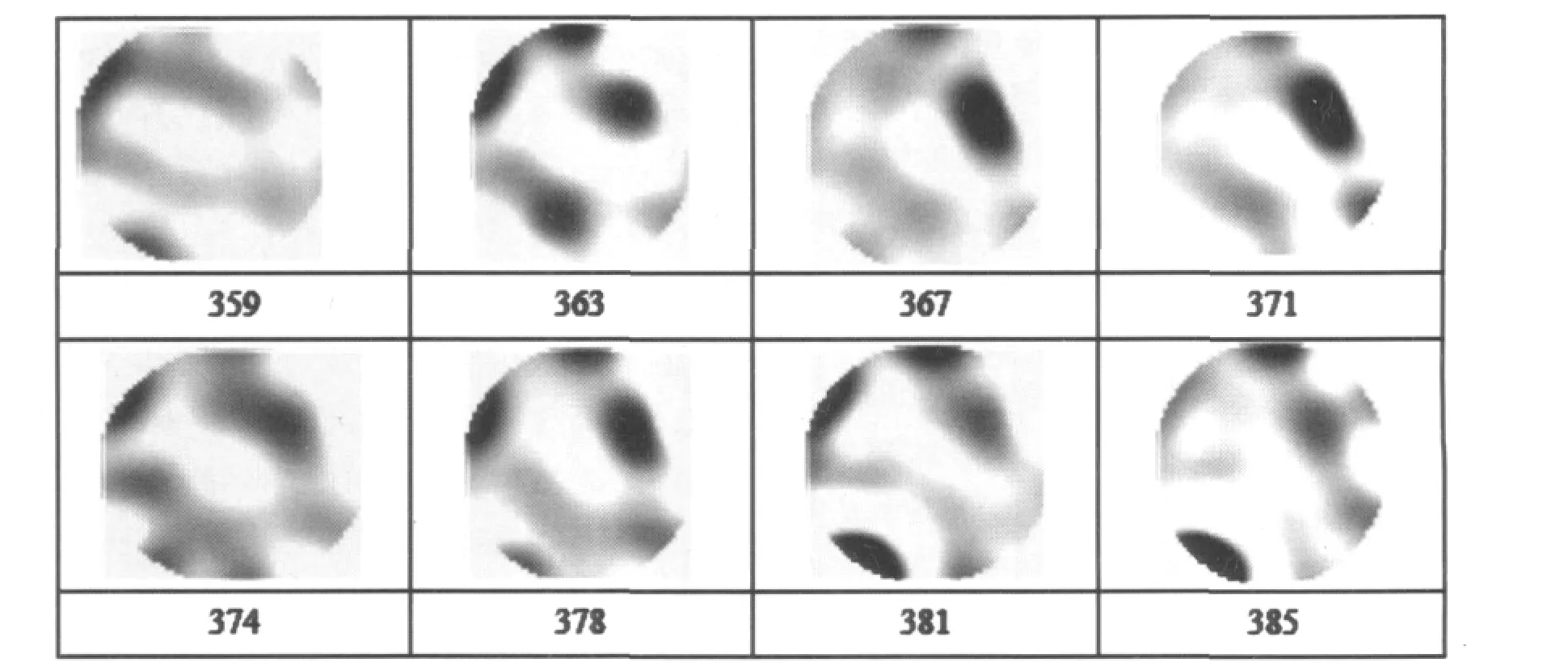
图1 固态分布
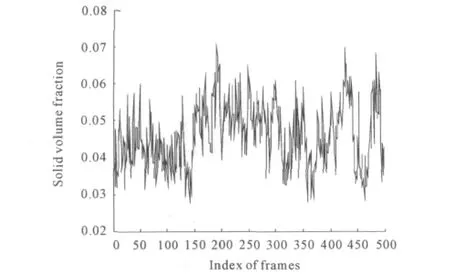
图2 某一检测周期内固相介质的体积分布
图1展现了由动态图像重建算法重构的横截面各相介质的分布特性。众所周知,ECT图像重建是典型的病态问题,因而需要提高重建图像的质量来确保稳定的检测结果。实验结果验证了动态图像重建算法的可行性,在标准Tikhonov正则化法的基础上得到ECT检测的稳定收敛解。此外,本实验也验证了ECT技术的快速在线采集检测特性,迅速捕捉到不同时刻横截面上介质的变化特性。图1中不同时刻对应的分布说明了这一点,并且在整个流动检测过程中,横截面上各相介质的分布具有实时变化性。当空气流动率为11 m/s时,横截面的固相介质分布相对分散,并且主要分布在提升管的中心或壁面。
另外,从图1中观察到,在本实验的运行条件下,横截面上固相介质的体积分数变动范围为3%~7%。得到流动管道横截面上固相介质的体积分数对实际HDCFB在提高系统效率、减少污染物排放方面具有非常重要的指导意义。图2中的横截面固相介质的体积分数波动复杂,因此选用去噪效果较好的小波多尺度分析法来分析实际的体积分数变动特性。图3~5显示了解析度为1~3对应的近似分析组分。从图3~5中可看出,随着解析度的增加,测量周期内固相介质的体积分数变动趋势及突变点逐渐明确地显现出来。特别地,图5中固相介质的体积分数变动趋势明显比图4清晰。此外,能够简单清楚地观察到固相介质的体积分数突变点。这充分表明,小波多尺度分析法能成功重现HDCFB中横截面固相介质的体积分数变动特性。
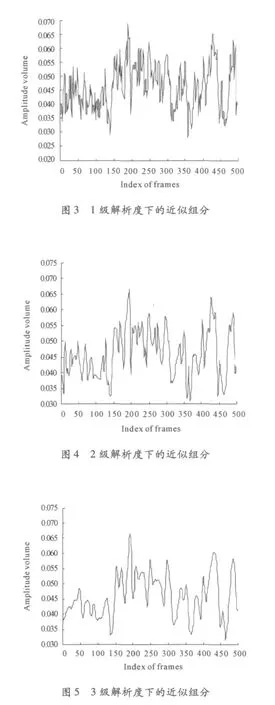
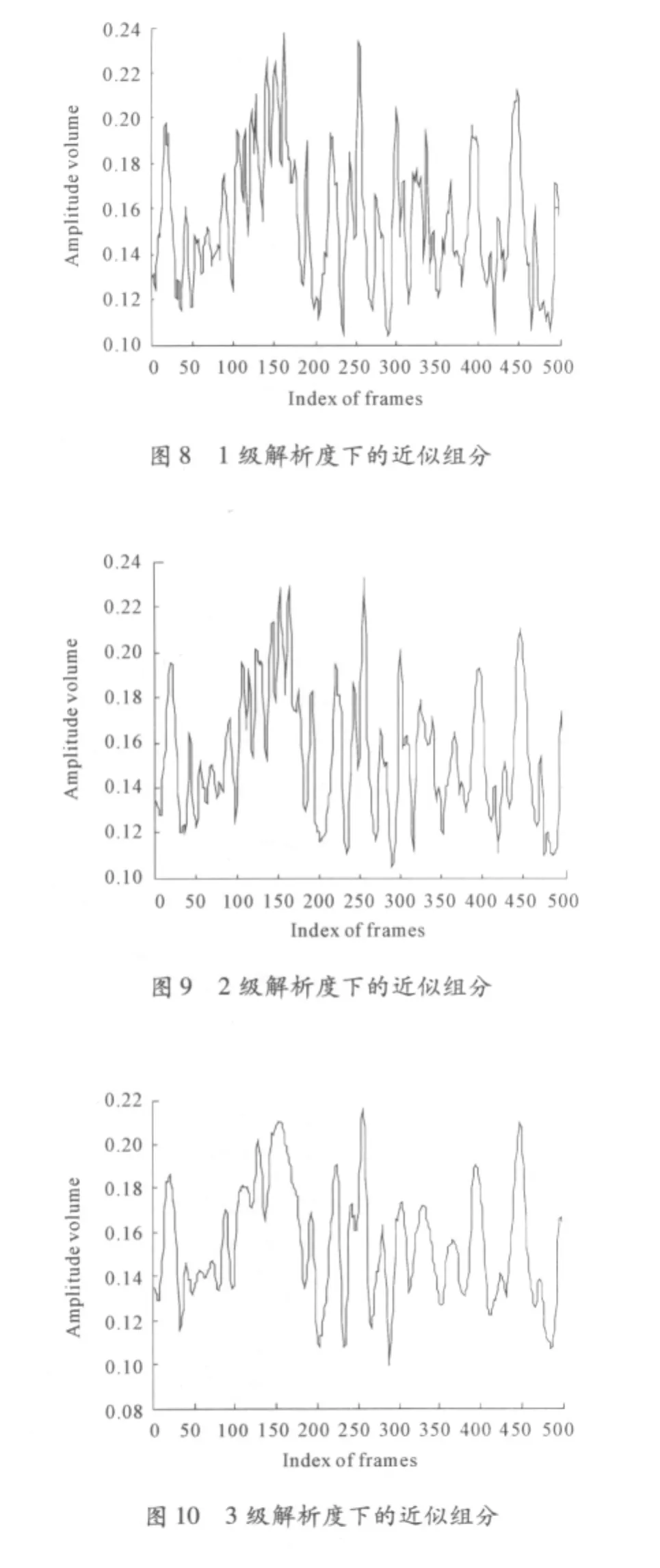
2)空气流速15 m/s。图6显示了当空气流速为15 m/s时通过广义动态图像重建算法得到的重建图像。图7展现了某一测量周期内对应的横截面上的固相介质体积分数变化趋势。依然用“Daubechies4”小波分析法多尺度分析横截面上固相介质体积分数变化波动趋势,其最大解析度为3。图8~10分别展示了解析度为1、2、3对应的近似组分。

图6 固态分布
图6的结果再次验证了广义动态图像重建算法在ECT重构横截面上各相介质分布的可行性。从图中可清晰地看到典型的中心环结构。由于低空气流速和固相介质的聚集特性,壁面区域的浓度相对较高,管道中心的浓度较低。研究表明,形成介质聚集的因素非常复杂,涉及到了气相和固相介质之间的可变应力、固相介质颗粒之间的可变应力,以及气固混合物与管壁之间的作用力。对于这个问题,有些研究者认为是固相介质颗粒间的非线性拖曳力导致了聚集现象的形成,有些研究者则认为是壁面对气固混合物移动的阻挡作用促使固相介质颗粒聚集现象的形成及中心环结构的出现,此外,还有研究者认为这种现象来源于固相介质颗粒间的无弹性碰撞。
图6还表明:由于复杂的物理机制,在HDCFB中,中心环结构会随时间变化而变化,是一个时变性过程,并且实验结果证明了ECT能够成功地检测气固两相流的流动结构及流型识别。
图7显示了当空气流速为15 m/s时某一测量周期内管道横截面上固相介质的体积分布波动情况。对应的固相介质体积分数的变动范围为11% ~24%。显然,固相介质体积分数的波动大部分由气固两相流系统内复杂的物理机制形成。
图8~10分别展现了分解度为1、2、3对应的近似组分,更加清晰地展现了固相介质体积分数的变化特性。随着解析度的增加,测量周期内体积分数的波动趋势和突变点逐渐清晰。图10明显比图9的结果清晰,更加容易确定突变点。

图7 不同帧下固态体积分布
4 结束语
高密度循环流化床已被广泛应用在燃烧、催化、合成等领域。高密度循环流化床内横截面固相介质的分布特性在提高系统效率和减少污染物排放方面发挥着至关重要的作用,因此需要实时地了解高密度循环流化床流动过程中横截面上固相介质的分布情况。本文在搭建实验平台的基础上,运用ECT技术可视化监测高密度循环流化床中的流动情况。对实验结果的处理选用新研究的广义动态图像重构算法,其集合了ECT测量信息和被测对象的空间约束、时间约束及流动变化的物理演化信息。动态实验研究表明,该算法成功解决了ECT的逆问题,并能给出一个确定的数值解。此外,实验结果表明,ECT在成功获得高密度循环流化床横截面固体介质的分布特性方面的可行性,并能成功获得截面固相介质流动的典型流动——核心结构分布方式。
由于ECT图像重建问题的病态性,对于一种算法完成不同的任务时可能会出现不同的数值解。对特定图像重建任务,相应的算法获取的信息主要来源于ECT测量系统和先前预定的信息。此外,ECT的成功使用对实验装置有明显依赖性,如设计的传感器、数据校准、数据阐释等,并在很大程度上依赖于特定的介质属性及几何性质。总之,ECT技术若要在实际工业应用中被广泛应用,需对其硬件和软件方面开展更多的研究。
[1]Harris A T,Davidson J F,Thorpe R B.The prediction of particle cluster properties in the near wall region of a vertical riser[J].Powder Technology,2002,127:128-143.
[2]Yerushalmi J,Turner D H,Squires A M.The fast fluidized bed[J].Industrial and Engineering Chemistry Process Design and Development,1976(15):47-53.
[3]Xie C G,Huang S M,Hoyle B S,et al.Electrical capacitance for flow imaging:system model for development of image reconstruction algorithms and design of primary sensors[J].IEE Proceedings-G,1992,139:89-98.
[4]Tikhonov A N,Arsenin V Y.Solution of Ill-Posed Problems[M].New York:V H Winston & Sons,1977.
[5]Landweber L.An iteration formula for fredholm integral equations of the first kind[J].American Journal of Mathematics,1951,73:615-624.
[6]Yang W Q,Spink D M,York T A,et al.An image recon-struction algorithm based on Landweber’s iteration method for electrical capacitance tomography[J].Measurement Science and Technology,1999(10):1065-1069.
[7]Jang J D,Lee S H,Kim K Y,et al.Modified iterative Landweber method in electrical capacitance tomography[J].Measurement Science and Technology,2006(17):1909-1917.
[8]Liu S,Fu L,Yang W Q,et al.Prior-online iteration for image reconstruction with electrical capacitance tomography[J].IEE Proceedings-Science,Measurement and Technology,2004,151:195-200.
[9]Yang W Q,Peng L H.Image reconstruction algorithms for electrical capacitance tomography[J].Measurement Science and Technology,2003(14):1-13.
[10]Mou C H,Peng L H,Yao D Y,et al.Image reconstruction using a genetic algorithm for electrical capacitance tomography[J].Tsinghua Science and Technology,2005(10):587-592.
[11]Takei M.GVSPM image reconstruction for capacitance CT images of particles in a vertical pipe and comparison with the conventional method[J].Measurement Science and Technology,2006(17):2104-2112.
[12]Soleimani M,Lionheart W R B.Nonlinear image reconstruction for electrical capacitance tomography using experimental data[J].Measurement Science and Technology,2005(16):1987-1996.
[13]Wang H X,Tang L,Cao Z.An image reconstruction algorithm based on total variation with adaptive mesh refinement for ECT[J].Flow Measurement and Instrumentation,2007(18):262-267.
[14]Lei J,Liu S,Guo H H,et al.An image reconstruction algorithm based on the regularized the semiparametric model for electrical capacitance tomography[J].Computers and MathematicswithApplications,2011,61:2843-2853.
[15]Ortiz-Aleman C,Martin R,Gamio J C.Reconstruction of permittivity images from capacitance tomography data by using very fast simulated annealing[J].Measurement Science and Technology,2004(15):1382-1390.
[16]Marashdeh Q,Warsito W,Fan L S,et al.Non-linear image reconstruction technique for ECT using a combined neural network approach[J].Measurement Science and Technology,2006(17):2097-2103.
[17]Warsito W,Fan L S.Neural network based multi-criterion optimization image reconstruction technique for imaging two-and three-phase flow systems using electrical capacitance tomography[J].Measurement Science and Technology,2001(12):2198-2210.
[18]Banasiak R,Soleimani M.Shape based reconstruction of experimental data in 3D electrical capacitance tomography[J].NDT&E International,2010,43:241-249.
[19]Kortschak B,Wegleiter H,Brandstatter B.Formulation of cost functionals for different measurement principles in nonlinear capacitance tomography[J].Measurement Science and Technology,2007(18):71-78.
[20]杨立峰,王亚非,周鹰.激光扫描声学显微镜层析成像技术研究[J].压电与声光,2007(5):612-614.
[21]马祥,丁杰雄,宋怡.微量样本中悬浮颗粒浓度的光纤检测装置研究[J].压电与声光,2011(2):188-191.
[22]姜发纲,张平,傅哲强.眼检光学相干层析成像系统及实验研究[J].激光杂志,2004(3):38-39.

