5A06铝合金中厚板反拉深变形行为
,,2,,2
(1 哈尔滨工业大学 金属精密热加工国家级重点实验室,哈尔滨150001;2 哈尔滨工业大学 材料科学与工程学院,哈尔滨150001)
5A06铝合金中厚板反拉深变形行为
张志超1,徐永超1,2,苑世剑1,2
(1哈尔滨工业大学金属精密热加工国家级重点实验室,哈尔滨150001;2哈尔滨工业大学材料科学与工程学院,哈尔滨150001)
中厚板变形过程中的弯曲和反弯曲效应影响其拉深变形能力。本工作以航空航天常用的5A06铝合金筒形件为研究对象,采用厚度为4.5mm的中厚板进行反拉深数值模拟和实验研究,分析了变形过程中应力、应变分布特点,讨论了3种凹模截面结构形式下的变形方式,以及应变路径随着凹模圆角变化规律。结果表明:凹模内圆角与直壁区过渡区在壁厚方向上存在应力和应变梯度,并在该处外侧产生最大径向拉应力,导致了拉深破裂的发生。采用半圆形凹模截面结构时,极限拉深深度达到203mm,相对于平面凹模结构增加了40%。半圆形凹模结构能减小弯曲效应,有效降低过渡区的应力梯度和最大应力数值,有利于提高5A06铝合金中厚板拉深变形能力。
铝合金;中厚板;拉深;破裂
铝合金材料比强度高、抗腐蚀性能优异,被广泛应用于航空、航天工业。随着节能减排的要求不断提高,铝合金深腔零件的整体成形得到越来越多的关注。这类零件高径比较大,拉深时悬空区受压应力易于起皱,凸模圆角处易于应力集中发生破裂,从而限制其成形。通常,采用充液拉深方法,利用高压流体介质,改善悬空区的受力状态,提高板料与凸模的摩擦保持效果,从而避免起皱和破裂的发生。然而,对于厚度超过3mm的深腔零件,通常采用分块成形拼装焊接的方法成形,获得的零件尺寸精度低、服役性能差[1,2]。为了提高拉深比,避免局部过度减薄破裂,可以采用二次拉深方法,实现大高径比深腔零件的成形。
二次拉深成形方法提高拉深比的原理是通过增加拉深道次,减小单道变形量,从而避免单道次成形时由于局部减薄严重而破裂[3]。通常,根据冲头与板料接触面是否发生变化,可以分为正二次拉深和反拉深[4]。反拉深相对于正二次拉深具有模具结构紧凑、模具定位简单、弯曲变形次数少等优点[5]。同时,由于反拉深板料与模具的包角为180°,板料与模具的摩擦阻力和弯曲抗力较大,法兰区抗皱能力提高,从而可以省略压边[6]。针对反拉深成形提出的理论模型,将径向应变近似分解为4个变量,分别为径向拉应变、弯曲应变、反弯曲应变和摩擦引起的剪切应变,在平衡方程的基础上考虑了应变强化和壁厚变化。采用该理论模型对反拉深过程的壁厚分布的预测结果表明,反拉深成形能明显提高板料拉深比、提高壁厚均匀性[7-10]。运用数值模拟的方法,考虑材料各向异性、材料应变强化以及应变路径变化对板料流动行为的影响,对反拉深变形过程中制耳现象以及壁厚分布进行了很好地预测,为优化反拉深变形工序提供了依据[11,12]。为了避免反拉深变形过程中发生破裂现象,辅助径向推力的充液反拉深成形方法被提出并进行了实验和数值模拟研究,结果表明,辅助径向推力能明显提高反拉深变形程度[13,14]。
上述研究主要针对薄板的反拉深变形行为的研究,忽略了板料弯曲效应。然而,对于中厚板变形,特别是反拉深变形,凹模圆角受到零件几何尺寸的限制,使得板料弯曲和反弯曲变形更加明显,弯曲效应不能忽略。本工作以筒形件为研究对象,对航空、航天常用的4.5mm厚5A06铝合金中厚板进行反拉深实验和数值模拟研究,采用3种不同的凹模结构形式,分析反拉深过程中应力、应变的分布特点,讨论凹模结构形式对板料应变路径的影响规律,揭示反拉深变形破裂机制。
1 试件及研究方案
本工作所用的退火态5A06铝合金板料,厚度为4.5mm。通过单向拉伸实验测得材料力学性能如表1所示。图1为板料真应力-应变曲线。由于受到零件几何尺寸限制,反拉深凹模内外侧圆角大小存在上限。根据凹模截面结构的不同,本工作采用3种凹模结构形式,分别为平面凹模结构、非对称曲面凹模结构和半圆形凹模结构,如图2所示。反拉深拉深比为1.5,冲头直径为300mm,冲头圆角半径为60mm,凸凹模间隙为1.42倍壁厚(6.4mm),为了便于讨论,板料分为筒底部、底部圆角区、直壁区、凹模内圆角区和凹模外圆角区5个部分,板料与凹模接触的表面为外表面,与凸模接触的表面为内表面,如图3所示。针对3种凹模结构形式,分别进行实验和数值模拟研究。数值模拟采用Abaqus/Explicit分析模块,材料模型服从Mises各向同性屈服准则,材料真实应力-应变关系如图1所示。板料选用轴对称实体单元,模具选用轴对称刚性壳单元。模具与板料之间为面接触,接触应力模型为各向同性库仑摩擦,摩擦因数为0.12。板料厚度方向上分布着9层网格,网格大小均匀,均为0.5mm。拉深行程为420mm,采用定压边间隙,压边间隙为1.2倍壁厚(5.4mm)。

表1 5A06铝合金板料力学性能Table 1 Mechanical properties of 5A06 aluminum alloy plate

图1 5A06铝合金中厚板真应力-应变曲线Fig.1 True stress-strain curve of 5A06 aluminum alloy plate
2 反拉深变形应力-应变分析
反拉深过程中,法兰区板料发生径向拉伸和切向压缩变形,流经凹模外圆角时伴随发生弯曲和反弯曲变形,流经凹模内圆角时伴随发生二次弯曲和反弯曲变形且弯曲方向与凹模外圆角处相同。当凹模外圆角区外侧的板料首次流经凹模内圆角成形得到直壁区之后,板料各区的应力、应变分布不再发生变化,反拉深过程达到稳定状态。采用数值模拟研究反拉深稳定状态下的应力、应变分布,对比不同凹模截面结构形式下最大应力、应变,提取典型点在整个拉深变形过程中的应变路径,分析凹模截面结构对应变路径的影响。

图2 凹模圆角截面结构形式 (a)平面凹模结构;(b)非对称曲面凹模结构;(c)半圆形凹模结构Fig.2 Die radius section structure types (a)plane die structure;(b)asymmetrical die structure;(c)semi-circle die structure

图3 模具几何尺寸示意图Fig.3 Schematic diagram of geometric parameters of dies
图4为平面凹模结构下反拉深后期板料应力分布,由图可知板料径向应力在厚度方向存在应力梯度。底部圆角区板料内外侧均为拉应力,且板料外侧大于内侧,应力梯度为110MPa。在凹模内圆角区近法兰一侧,板料外侧为压应力,内侧为拉应力,在厚度方向的应力梯度为831MPa。在凹模内圆角与直壁段过渡处,板料内侧为压应力,外侧为拉应力,应力梯度为1292MPa。同样,在凹模外圆角区,板料厚度方向存在应力梯度,与凹模内圆角区相比较小。凹模内、外圆角区板料发生弯曲和反弯曲从而导致该区径向应力梯度在厚度方向较大。凹模内圆角与直壁区过渡处板料的外侧,存在最大的径向拉应力,其值为666MPa。由于变形区材料硬化导致变形抗力增大,同时,该处发生反弯曲在板料外侧产生附加拉应力,从而导致该处板料外侧存在最大的径向拉应力。如图4所示,切向应力在筒底部均匀分布,在已成形的直壁区和凹模内、外侧圆角区沿厚度方向存在应力梯度。在凹模内圆角与直壁区过渡处,板料外侧拉应力为315MPa,内侧压应力为463MPa,厚度方向应力梯度最大为778MPa。该处板料发生反弯曲变形,使得外侧产生拉应力,内侧产生压应力,从而在厚度方向上产生最大切向应力梯度。由上述结果可知,由于反弯曲变形,在凹模内圆角与直壁区过渡处外侧存在最大的径向拉应力和切向拉应力,并且在厚度方向存在应力梯度。凹模内圆角与直壁区过渡处外侧的最大径向拉应力易于导致该处板料发生破裂。
图5为平面凹模结构下反拉深后期板料应变分布。由该图可知,筒底部径向应变均匀分布,径向应变为0.04。底部圆角处由于弯曲效应在厚度方向存在径向应变梯度,板料外侧拉应变大于内侧,应变梯度为0.05。直壁区在厚度方向上存在梯度,板料外侧应变大于内侧,应变梯度最大为0.15。在凹模内、外圆角处由于弯曲效应同样存在径向应变梯度,且径向应变梯度相等为0.13。板料切向应变分布相对较均匀,仅在底部圆角和凹模圆角处存在较小应变梯度。由上述结果可知,反拉深过程中弯曲作用明显,导致了厚度方向存在应变梯度,应变梯度最大值位于凹模内圆角与直壁区过渡处,该处板料外侧径向应变大于内侧,表明拉深过程中易于在该处发生破裂。
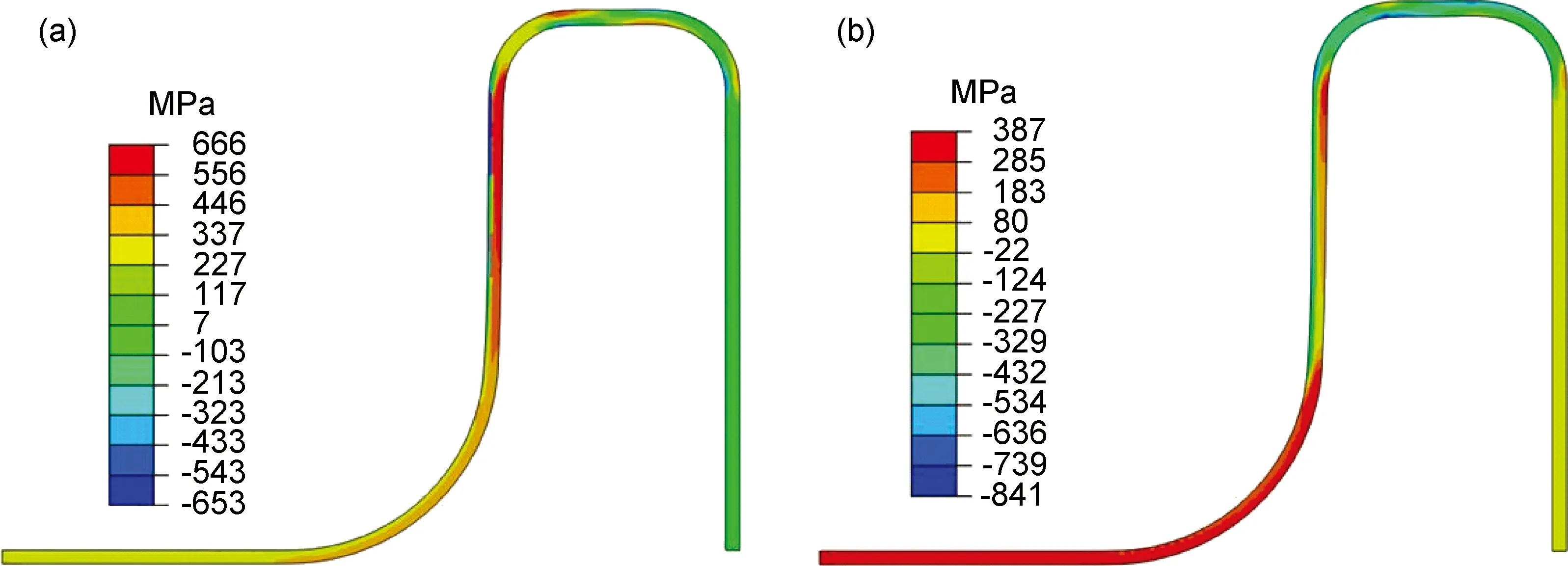
图4 反拉深后期应力分布 (a)径向应力;(b)切向应力Fig.4 Stress distributions at the end stage of reverse deep drawing process (a)radial stress;(b)tangential stress
图6为拉深变形过程中板料典型位置的应变路径。图中εr为径向应变,εt为切向应变。由该图可知,筒底部A处中性层点按双向等拉线性应变路径变化。拉深过程中,该点变形量较小。凹模内圆角区B处中性层点在拉深开始之后,经由凹模内圆角流入凹模,径向发生拉伸变形,切向发生压缩变形。拉深过程中,该点偏离线性应变路径。凹模外圆角区内侧C处中性层点在拉深过程中发生径向拉伸切向压缩变形,加载路径为线性,当流经凹模内圆角时,偏离线性应变路径。凹模外圆角区外侧D处中性层点在拉深过程中,首先流经凹模外侧圆角,受弯曲变形的影响偏离线性应变路径。当流经凹模内圆角时,偏离更加明显,径向拉应变显著增大,而切向应变增大较小。

图5 反拉深后期应变分布 (a)径向应变;(b)切向应变Fig.5 Strain distributions at the end stage of reverse deep drawing process (a)radial strain;(b)tangential strain

图6 反拉深过程典型点应变路径Fig.6 Strain paths of typical points during reverse deep drawing process
由前述应力分布可知,反拉深稳定状态时,在凹模内圆角与直壁区过渡处板料外侧存在最大径向和切向应力,导致该处易于发生破裂。图7为不同凹模结构形式下反拉深稳定状态下的最大径向应力和切向应力。由该图可知,采用平面凹模结构时,最大径向拉应力为666MPa,最大切向拉应力为319MPa。采用非对称曲面凹模结构时,最大径向拉应力为576MPa,最大切向拉应力为236MPa,相对于平面凹模结构分别下降13.5%和26.0%。采用半圆形凹模圆角时,最大径向拉应力为514MPa,最大切向拉应力为152MPa,相对于平面凹模圆角分别下降22.8%和52.3%。由上述可知,改变凹模圆角结构形式能显著减小反拉深稳定状态下的最大径向拉应力和切向拉应力,采用半圆形凹模圆角时,径向拉应力和切向拉应力最小,从而减缓破裂的发生,利于极限拉深变形能力的提高。

图7 不同凹模截面结构形式下最大径向和切向应力Fig.7 Maximum radial and tangential stress under different die structures
图8所示为不同凹模截面结构形式下凹模外圆角区D处板料内外侧点及中性层点的应变路径。由该图可知,板料中性层点,近似为线性应变路径,外侧点和内侧点应变路径则偏离线性路径,随着拉深的进行,不断发生变化。应变路径发生变化时,铝合金板料均匀变形能力下降,从而导致变形过程中破裂现象提前发生[15-17]。采用平面凹模结构时,板料内、外侧点偏离线性应变路径,往复变化,从而严重降低了板料的均匀变形能力。采用不对称凹模结构相对于平面凹模结构有明显改善,当变形量达到一定值之后,厚度方向各点应变路径基本一致,并保持线性变化。采用半圆形凹模结构时,板料内、外侧点基本保持线性路径,变形过程中,厚度方向各点的变形基本同步。由上述结果可知,采用半圆形凹模结构能提高板料的均匀变形能力,从而利于板料的拉深变形。
3 5A06铝合金反拉深实验
图9为不同凹模结构的反拉深试件,图10为相应的极限拉深深度。由图9可知,不同凹模结构形式下,反拉深均发生破裂,破裂位置都位于凹模内圆角区与直壁区过渡处。由图10可知,当选用平面凹模结构时,极限拉深深度为145mm;采用非对称曲面凹模结构时,极限拉深深度为168mm;采用半圆形凹模结构时,极限拉深深度为203mm,相对于平面凹模结构,增长了40%。根据前述模拟结果可知,由于反弯曲作用,在凹模内圆角区与直壁区过渡处板料外侧存在最大径向拉应力,该拉应力引起拉深破裂的发生。同时,板料在流经凹模内、外圆角时,偏离线性应变路径,导致均匀塑性变形能力的降低,使得内圆角区与直壁区过渡处板料易于发生破裂。反弯曲作用受到凹模内圆角大小的影响,凹模内圆角越大,反弯曲作用越不明显。然而,由于受零件几何尺寸的限制,凹模内圆角不能无限增大,通过改变内外圆角大小的组合可以减小反弯曲造成的最大径向拉应力,改善内外圆角对应变路径的影响。当采用半圆形凹模结构时,最大径向拉应力最小,板料内外侧的应变路径基本上为线性路径,利于塑性变形能力的提高,反拉深极限拉深深度最大。
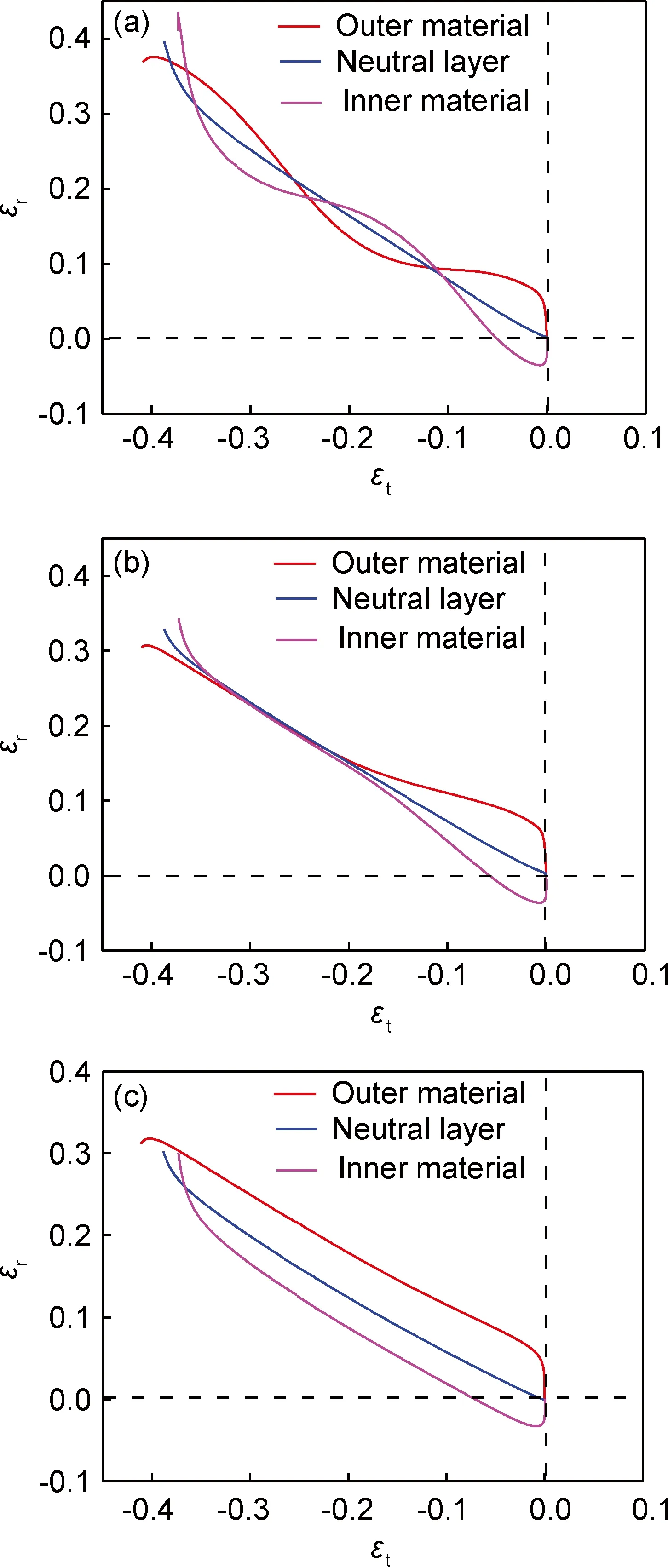
图8 不同凹模截面结构下应变路径 (a)平面凹模结构;(b)非对称曲面凹模结构;(c)半圆形凹模结构Fig.8 Strain paths of the typical points under different die structures (a)plane die structure;(b)non-symmetrical die structure;(c)semi-circle die structure

图9 不同凹模截面结构形式下破裂试件 (a)平面凹模结构;(b)非对称曲面凹模结构;(c)半圆形凹模结构Fig.9 Experiment results of different die radius (a)plane die structure;(b)non-symmetrical die structure;(c)semi-circle die structure

图10 不同凹模截面结构形式下极限拉深深度Fig.10 Limited punch stroke under different die structures
4 结论
(1)由于弯曲效应,在厚度方向存在应力梯度,应力梯度最大值位于凹模内圆角与直壁区过渡处,该处板料内侧存在径向和切向压应力,外侧存在径向和切向的拉应力。同时,在厚度方向上也存在应变梯度,板料外侧的径向应变大于板料内侧。应变梯度最大值位置同样位于凹模内圆角与直壁区过渡处。
(2)板料不同位置点的应变路径不同,筒底部应变类型为双向等拉,变形过程中保持线性应变路径。法兰处材料应变类型为一拉一压,经由凹模外圆角和内圆角变形时,偏离线性应变路径。其中,凹模内圆角对应变路径影响显著。采用平面凹模结构时,板料内外侧点偏离线性应变路径最为明显。采用半圆形凹模圆角时,板料各点延线性应变路径变化,利于板料塑性变形。
(3)采用半圆形凹模结构时,极限成形深度与平面凹模结构和非对称曲面凹模结构相比最小,分别减小了22.8%和13.5%。采用半圆形凹模结构时,极限拉深深度为203mm,相对于平面凹模结构和非对称曲面凹模结构分别增长了40%和16%。改变凹模截面结构形式,能显著减小最大拉应力,提高极限拉深变形能力。
[1] 董鹏, 孙大千, 李洪梅, 等. 6005A-T6 铝合金搅拌摩擦焊接头组织与力学性能特征[J]. 材料工程, 2012(4): 27-31.
DONG P, SUN D Q, LI H M, et al. Microstructural and mechanical characteristics of friction stir welded 6005A-T6 aluminium alloy[J]. Journal of Materials Engineering, 2012(4): 27-31.
[2] 刘杰, 杨景宏, 韩凤武, 等. 厚板铝合金搅拌摩擦焊匙孔补焊接头组织与性能[J]. 材料工程, 2012(7): 29-33.
LIU J, YANG J H, HAN F W, et al. Microstructures and properties of thickness aluminium alloy eleocellarium repairing welding joint by friction stir welding[J]. Journal of Materials Engineering, 2012(7): 29-33.
[3] ESCHE S K, AHMETOGLU M A, KINZEL G L, et al. Numerical and experimental investigation of redrawing of sheet metals[J]. Journal of Materials Processing Technology, 2000, 98(1): 17-24.
[4] ESCHE S K, KHAMITKAR S, KINZEL G L, et al. Process and die design for multi-step forming of round parts from sheet metal[J]. Journal of Materials Processing Technology, 1996, 59(1): 24-33.
[5] PARSA M H, YAMAGUCHI K, TAKAKURA N, et al. Consideration of the re-drawing of sheet metals based on finite element simulation[J]. Journal of Materials Processing Technology, 1994, 47(1/2):87-101.
[6] 江学强, 吉卫, 曹海桥, 等. 厚壁筒形件热拉深成形数值模拟及工艺研究[J]. 热加工工艺, 2014, 43(11): 148-150.
JIANG X Q, JI W, CAO H Q, et al. Numerical simulation and technical study of hot drawing forming thick-wall cylinder[J]. Hot Working Technology, 2014, 43(11): 148-150.
[7] CHUNG S Y. Stress analysis of reverse redrawing of cylindrical shells[J]. Sheet Metal Industries, 1951(28):453-458.
[8] ZHARKOV V A. Theory of the drawing of cylindrical parts from sheet materials[J]. J Mater Process Technol, 1992,(31):379-392.
[9] CHANG D F, WANG J E. Wall thickness distribution analysis of a drawn-redrawn can[J]. Transactions of the North American Manufacturing Research Institution of SME, 1996, 24:125-130.
[10] MAJLESSI S A, LEE D. Development of multistage sheet metal forming analysis method[J]. Journal of Materials Shaping Technology, 1988, 6(1): 41-54.
[11] PAUNOIU V, RAMOS M G, MANGAS V L. Experimental and numerical analysis of multistage deep drawing[J]. The Annals of "Dunărea de Jos" University of Galati: Fascicle V, 2012, 1: 79-84.
[12] THUILLIER S, MANACH P Y, MENEZES L F, et al. Experimental and numerical study of reverse re-drawing of anisotropic sheet metals[J]. Journal of Materials Processing Technology, 2002, 125: 764-771.
[13] ZHAO S D, ZHANG Z Y, ZHANG Y, et al. The study on forming principle in the process of hydro-mechanical reverse deep drawing with axial pushing force for cylindrical cups[J]. Journal of Materials Processing Technology, 2007, 187: 300-303.
[14] WANG H, GAO L, CHEN M. Hydrodynamic deep drawing process assisted by radial pressure with inward flowing liquid[J]. International Journal of Mechanical Sciences, 2011, 53(9): 793-799.
[15] GRAF A, HOSFORD W. The influence of strain-path changes on forming limit diagrams of A1 6111 T4[J]. International Journal of Mechanical Sciences, 1994, 36(10): 897-910.
[16] STOUGHTON T B, ZHU X. Review of theoretical models of the strain-based FLD and their relevance to the stress-based FLD[J]. International Journal of Plasticity, 2004, 20(8): 1463-1486.
[17] KURODA M, TVERGAARD V. Effect of strain path change on limits to ductility of anisotropic metal sheets[J]. International Journal of Mechanical Sciences, 2000, 42(5): 867-887.
(本文责编:齐书涵)
DeformationBehaviorofReverseDeepDrawingof5A06AluminumAlloyPlate
ZHANGZhi-chao1,XUYong-chao1,2,YUANShi-jian1,2
(1NationalKeyLaboratoryofPrecisionHotProcessingofMetals,HarbinInstituteofTechnology,Harbin150001,China;2SchoolofMaterialsScienceandEngineering,HarbinInstituteofTechnology,Harbin150001,China)
The limit drawing ratio is influenced by the bending and unbending effect during reverse deep drawing of plate. The 5A06 aluminum alloy plate widely applied in aerospace industry was used, and the reverse deep drawing of the 4.5mm thick plate was investigated experimentally and numerically. The stress and strain distributions of plate were analyzed, the deformation behaviour was discussed for three types of cross section of die during the reverse deep drawing process; moreover, the changing rule of strain paths with the die profile was also discussed. Results show that a maximum radial stress is induced by the bending effect at the transient region between the inside die radius and straight wall, where a radial stress and strain gradient along the thickness direction appears and the fracture is easy to occur. For the semi-circle profiled die structure, the limited punch stroke is 203mm which is increased by 40% than that for the die with a planar profile section. The semi-circle profiled die structure can reduce the bending effect, effectively reduce the stress gradient and the maximum stress value in the transient region, and is helpful to improve the limit drawing ratio of the 5A06 aluminum alloy plate.
aluminum alloy;plate;deep drawing;fracture
10.11868/j.issn.1001-4381.2015.000822
TG386.3
: A
: 1001-4381(2017)09-0101-07
国家自然科学基金资助项目(51375114);长江学者和创新团队发展计划资助项目(IRT1229)
2015-07-01;
:2017-06-12
徐永超(1974-),男,教授,博导,主要从事板材流体高压成形工艺与装备、航空航天轻质难变形合金热成形工艺与装备研究,联系地址:哈尔滨市南岗区西大直街92号哈尔滨工业大学材料学院420室(150001),E-mail: yongchaoxu@hit.edu.cn

