Banach空间中一类无穷时滞分数阶微分方程

徐小平，毋绪道，王杰瑛，董琪翔＊

（1．扬州大学 数学科学学院，江苏 扬州225002；2．南通职业大学 基础部，江苏 南通226007；3．焦作师范高等专科学校 数学系，河南 焦作454001）

分数阶微积分是经典整数阶微积分的推广．由于分数阶微积分非常适用于刻画具有记忆和遗传性质的材料和过程，因此分数阶微分方程越来越多地被用来描述光学、热学系统，流变学、材料和力学系统，信号处理和系统辨识，控制和机器人及其他应用领域中的问题［1－3］．有关时滞型微分方程的研究始于20世纪70年代，由于这类方程能更真实地反映客观变化过程，故近年来受到诸多学者的关注，而且有了较丰富的研究成果［4－8］．

设X 为一个Banach空间，考虑分数阶无穷时滞微分方程

其中Dα为Riemann－Liouville 导数，0＜α＜1，f：［0，T］×B→X 为已知函数，B 为相空间，yt：（－∞，0］→X 定义为yt（θ）＝y（t＋θ），θ∈（－∞，0］．BENCHOHRA 等［9］在实数域R 中讨论了方程（1）～（2），研究了当f 连续且满足次线性增长等条件时方程解的存在性．在本文中，笔者拟在Banach空间X 中利用非紧测度理论、Darbo不动点定理等讨论方程（1）～（2）解的存在性，以改进和推广已有的相关结论．

1 预备知识

设X 为一个Banach空间，并赋予其通常意义下的范数‖·‖，C（［a，b］；X）表示定义在区间［a，b］，取值于X 的连续函数全体按范数‖x‖＝sup｛｜x（s）｜：s∈［a，b］｝构成的Banach空间．

定义1［10］由（－∞，0］到X 的一些函数构成的集合B 赋予半范数‖·‖B，称为一个相空间，并满足下列公理：

A1：若y：（－∞，T］→X，T＞0，使得y0∈B，y｜［0，T］连续，则∀t∈［0，T］，有（i）yt∈B；（ii）‖yt‖B≤K（t）sup｛｜y（s）｜：0≤s≤t｝＋M（t）‖y0‖B；（iii）｜y（t）｜≤H‖yt‖B，其中H≥0为常数，K，M：［0，＋∞）→［0，＋∞），K 连续，M 局部有界，H，K，M 均独立于y（·）；

A2：对A1中的函数y（·），映射t∈［0，T］→yt连续；

A3：空间B完备．

定义2［3］13设定义算子为称为函数h的α阶（分数阶）积分，也称Iαa为分数阶积分算子，其中Γ（·）为gamma函数，即

关于分数阶导数的定义有多种形式，采用较多的是下面的Caputo定义和Riemann－Liouville定义．

定义3［3］27，501）（Caputo分数阶导数）设h：［a，b］→R，α＞0，n＝［α］＋1，n－1＜α＜n，定义称上式为h在t点的α阶Caputo（分数阶）导数，也称CDαa＋h（t）为Caputo分数阶微分算子．

2）（Riemann－Liouville分数阶导数）设h：［a，b］→R，α＞0，n＝［α］＋1，n－1＜α＜n，定义称上式为h在t点的α阶Riemann－Liouville（分数阶）导数，也称RDαa＋h（t）为Riemann－Liouville分数阶微分算子．

当α为正整数时，CDαa＋h（t）和RDαa＋h（t）即为整数阶导数h（α）（t），显然Riemann－Liouville微分算子对常数的分数阶导数不一定为0，而Caputo 微分算子对常数的导数都为0，但是Riemann－Liouville导数与Caputo导数在起始点a处的情形是不一样的，因此在具体问题中应根据实际情况来选择．为方便起见，以下用Dα表示Riemann－Liouville微分算子RDα0．

定义4［11］6设Y 是实Banach空间，B 是Y 中的有界子集，令χY（B）＝inf｛ε＞0；B 在Y 中被有限个半径不小于ε的球所覆盖｝，称χY（B）为B 在Y 中的Hausdorff非紧性测度．

定义5［11］15设Y 是一实Banach空间，映射Q：W ⊂Y →Y 连续有界．若存在正常数k＜1，使得对任意有界集C ⊆W，都满足χY（QC）≤kχY（C），则称Q 是W 上的严格集压缩映射．

引理1［11］9－14设Y，Z 是Banach空间，B，C 是Y 中的有界集，λ是一实数，则

1）χY（B）＝0⇔B 是相对紧集；

2）χY（B）＝χY（¯B）＝χY（conv B），¯B 和conv B 分别为B 的闭包和凸包；

3）B ⊆C⇒χY（B）≤χY（C）；

4）χY（B＋C）≤χY（B）＋χY（C），其中B＋C ＝｛x＋y：x ∈B，y ∈C｝；

5）χY（B∪C）≤max｛χY（B），χY（C）｝；

6）χY（λB）＝｜λ｜χY（B），其中λ∈R，λB ＝｛x ＝λz：z∈B｝；

7）若映射Q：D（Q）⊂Y →Z 是Lipschitz连续的，且Lipschitz常数为k，则对任意有界集B ⊂D（Q），有χZ（QB）≤kχY（B）．

引理2［11］60，69若W ⊆C（［a，b］；X）有界，则对任意的t∈［a，b］，有χ（W（t））≤χC（W），其中W（t）＝｛y（t）：y ∈W｝⊆X；进一步地，若W 还等度连续，则χ（W（t））在［a，b］上连续，χC（W）＝sup｛χ（W（t））：t∈［a，b］｝，且

定理1［11］17（Darbo不动点定理） 设Y 为Banach空间，映射Γ：Y →Y 连续．若Γ是严格集压缩映射，且存在有界闭凸集W ⊆Y，使得ΓW ⊂W，则Γ 在W 上有不动点．

2 主要结果

定义6 设函数u：（－∞，T］→X，如果u｜（－∞，0］＝φ，u｜［0，T］连续，且对t∈［0，T］，u（·）满足积分方程则称u为方程（1）～（2）的一个mild解．

以下设1＜p＜1／（1－α），1／p＋1／q＝1，记KT＝sup｛K（t）：t∈［0，T］｝，MT＝sup｛M（t）：t∈［0，T］｝，a＝［（α－1）p＋1］／p，b＝［（α－1）p＋1］1／p，并假设以下条件成立．

H1：f：［0，T］×B→X 满足Caratheodory条件，即对任意的y∈B，f（·，y）：［0，T］→X 可测且f（·，y）∈Lq（［0，T］；X），对几乎所有的t∈［0，T］，f（t，·）：B→X 连续；

H2：存在函数h∈Lq（［0，T］；R＋），连续非减函数Ω：［0，＋∞）→［0，＋∞），使得‖f（t，v）‖ ≤h（t）Ω（‖v‖B），t∈［0，T］，v∈B；H3：存 在 函 数η ∈Lq（［0，T］；R＋），使 得 对 任 何 有 界 集D ⊂B，χ（f（t，D））≤η（t）·sup－∞＜θ≤0χ（D（θ）），其中D（θ）＝｛u（θ）：u∈D｝；

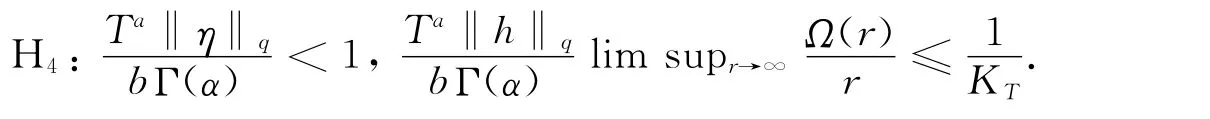
定理2若条件H1～H4满足，则对任意φ∈B，φ（0）＝0，方程（1）～（2）至少有一个mild解．

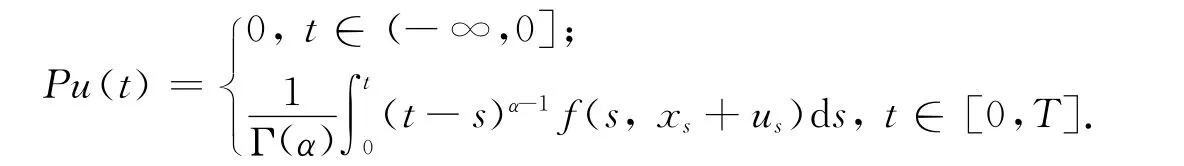
容易证明若P 有不动点u，令y（t）＝x（t）＋u（t），t∈（－∞，T］，则y即为方程（1）～（2）的一个适度解．下面分4步进行证明．

第1步：证明P 在C0上是连续的．设｛un｝⊂C0，u∈C0，使得在C0中un→u（n→∞），则对任意t∈［0，T］，有

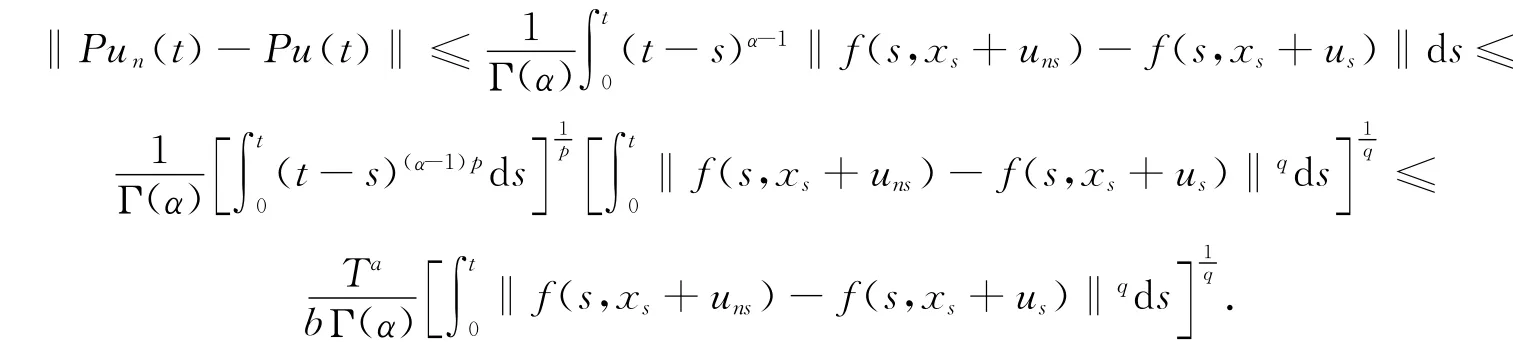
由公理A1可知，对任意s∈［0，t］⊂［0，T］，有

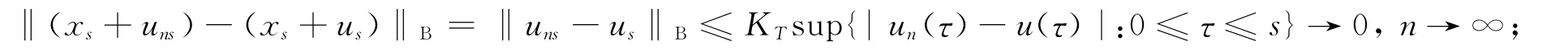
因此，由条件H1知，对a．e．s∈［0，T］，有‖f（s，xs＋uns）－f（s，xs＋us）‖ →0，n→∞；从而由控制收敛定理知，∀t∈［0，T］，有再对t取上确界，即得Pun→Pu（n→∞）；因此，P 在C0上是连续的．

第2步：证明∃r＞0，使得PBr⊂Br．由条件H4知因此存在r＞0，使得作则对任意u∈Br，s∈［0，T］，有

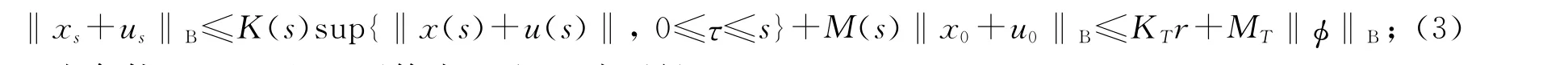
所以，由条件H2，Hölder不等式以及（3）式可得

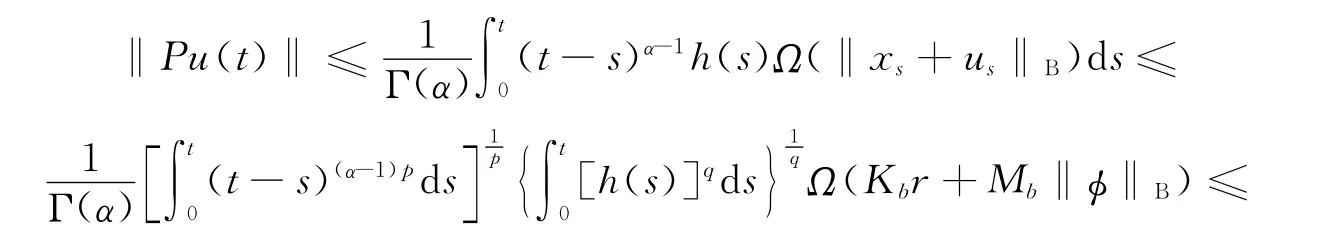
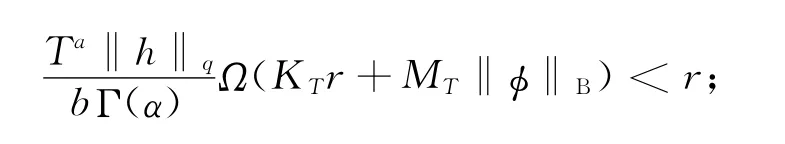
再对t∈［0，T］取上确界，即得Pu ∈Br，因此PBr⊂Br．

第3步：证明对有界集B ⊂C0，PB 为等度连续集．由于B 有界，故存在r＞0，使得∀u∈B，‖u‖C0≤r．任取t1，t2∈［0，T］，可设t1＜t2，由H2，Hölder不等式及（3）式可得

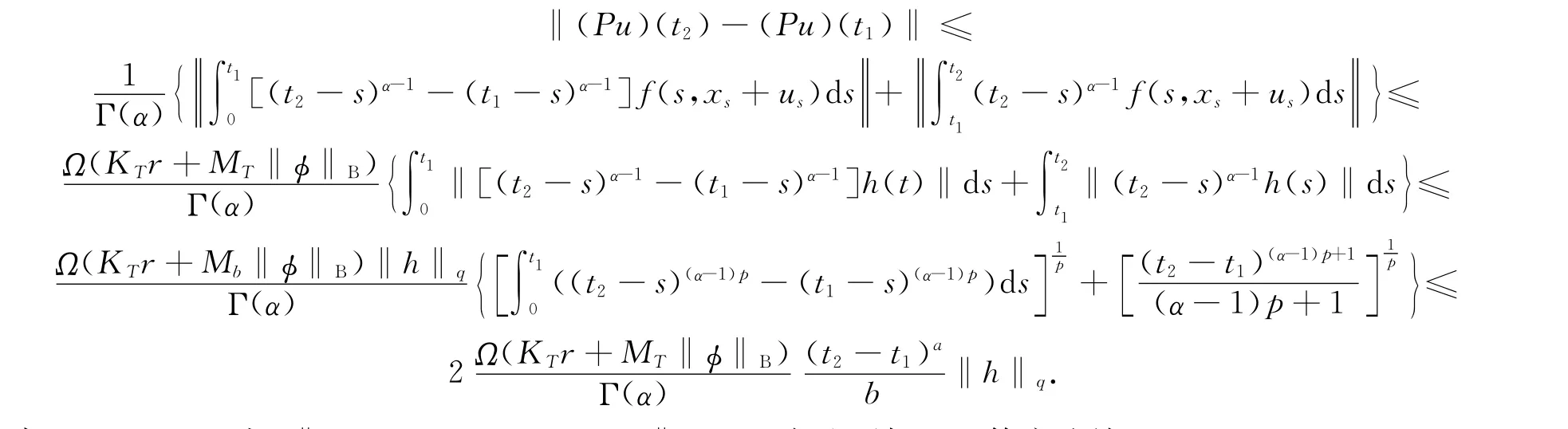
当t2－t1→0时，‖（Pu）（t2）－（Pu）（t1）‖ →0．由此可知PB 等度连续．

第4步：证明P 在PBr上严格集压缩．∀B ⊂PBr，B 等度连续，由H3可得

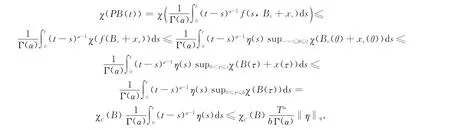
由此可知，据Darbo不动点定理（定理1），P 在C0上有不动点，记此不动点为u，则y＝x＋u即为方程（1）～（2）的适度解．由H4知

［1］ MILLER K S，ROSS B．An introduction to the fractional calculus and fractional differential equation［M］．New York：John Wiley ＆Sons，1993：1－37．

［2］ BAJLEKOVA E G．Fractional evolution equations in Banach spaces［M］．Eindhoven：University Press Facilities，Eindhoven University of Technology，2001：1－18．

［3］ DIETHELM K．The analysis of fractional differential equations：an application－oriented exposition using differential operators of Caputo type［M］．Berlin：Springer，2010：13－132．

［4］ DONG Qixiang，LI Gang．Existence of solutions for semilinear differential equations with nonlocal conditions in Banach spaces［J］．Electron J Qual Theory Differ Equ，2009（47）：1－13．

［5］ DONG Qixiang，FAN Zhenbin，LI Gang．Existence of solutions to nonlocal neutral functional differential and integrodifferdntial equations［J］．Int J Nonlinear Sci，2008，5（2）：140－151．

［6］ 毋光先，董琪翔，李刚．Banach 空间中双扰动无穷时滞微分方程［J］．南京大学学报：数学半年刊，2010，27（1）：124－133．

［7］ 张进，练婷婷，李刚．Banach空间中具有非局部条件的积分微分方程［J］．扬州大学学报：自然科学版，2007，10（4）：21－25．

［8］ 练婷婷，张进，李刚．Banach空间中时滞型多值积分微分包含［J］．扬州大学学报：自然科学版，2008，11（1）：5－9．

［9］ BENCHOHRA M，HENDERSON J，NTOUYAS S K，et al．Existence results for fractional order functional differential equations with infinite delay［J］．J Math Anal Appl，2008，338（2）：1340－1350．

［10］ HINO N，MURAKAMI S，NAITO T．Functional differential equations with infinite delay［M］／／Lecture Notes in Mathematics，Vol．1473．Berlin：Springer，1991：4－5．

［11］ BANAS J，GOEBEL K．Measure of noncompactness in Banach space［M］／／BANAS J．Lecture Notes in Pure and Applied Mathematics，60．New York：Dekker，1980：4－138．