与一类积分算子相关的sandwich－type定理

杨 清

（扬州大学 数学科学学院，江苏 扬州225002）

在复分析中，有关解析函数的性质和微分从属的研究已经取得了许多重要结果．例如：刘金林［1］，施冬芳［2］等分别对含有某些积分算子和Noor积分算子的解析函数进行了深刻阐述；ALI［3］，MILLER［4］等得到了微分从属的一些性质和定理．近年来，越来越多的学者致力于研究微分从属的对偶问题，由此得出某些特定的解析函数具有保持微分从属和微分超属的性质，从而得到sandwich－type定理．例如：BULBOACǍ［5－6］给出了微分超属的若干结论；ALI［7］，AOUF［8］等分别论证了含有乘数变换的解析函数和含有某些高阶线性算子的p 叶函数具有保持微分从属和微分超属的性质；SHANMUGAM 等［9］提出了含有Dziok－Srivastava算子的解析函数也具有此性质，从而得到Dziok－Srivastava算子的sandwich－type定理．本文在前人工作的基础上，笔者拟重新定义一类积分算子，记为I，通过研究I具有保持某一类解析函数从属和超属的性质，得到I的sandwich－type定理．

1 预备知识和相关引理

本文中H 表示定义在单位圆U＝｛z∈C：｜z｜＜1｝内的全体解析函数．对于任意a∈C，H［a，n］为H 的子类，为H［a，p］的子类，Ap＝｛f∈H：f（z）＝zp＋ap＋1zp＋1＋…｝．对于任意f∈Ap，定义一类积分算子，记为I，

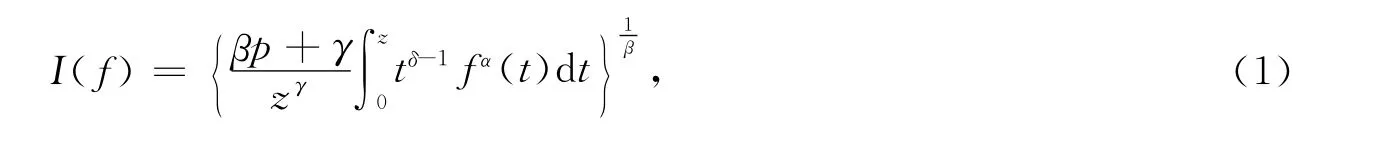
定义1［8］629上单叶解析｝，这里且满足

定义2［10］919设φ：C2→C 和h 是单叶函数．如果p 是解析函数并且满足微分从属φ（p（z），zp′（z））≺h（z），那么p 称为该微分从属的一个解．

定义3［10］919设φ：C2→C和h是解析函数．如果p 和φ（p（z），zp′（z））是单叶函数并且满足微分超属h（z）≺φ（p（z），zp′（z）），那么p 称为该微分超属的一个解．

定义4L（z，t）是定义在U×［0，∞）上的函数，如果对所有的t∈［0，∞），L（·，t）在U 上单叶解析，对所有的z∈U，L（z，·）在［0，∞）上连续可微且L（z，s）≺L（z，t）（0≤s＜t），那么L（z，t）称为定义在U×［0，∞）上的从属链．

引理1［11］431假设函数h：C2→C满足条件Re｛h（i s，t）｝≤0，其中s∈R，t≤－n（1＋s2）／2，n是正整数．若函数p（z）＝1＋pnzn＋…在U 内解析，并且满足Re｛h（p（z），zp′（z））｝＞0（z∈U），则有Re｛p（z）｝＞0．

引理2［11］431设β，γ∈C且β≠0；h∈H，h（0）＝c．若Re｛βh（z）＋γ｝＞0（z∈U），则q（z）＋zq′（z）／［βq（z）＋γ］＝h（z）的解q（q（0）＝c）解析并且满足Re｛βq（z）＋γ｝＞0（z∈U）．

引理3［11］432L（z，t）＝a1（t）z＋…，a1（t）≠0（limt→∞｜a1（t）｜＝∞）是 从 属 链 当 且 仅 当

引理4［11］432q∈H［a，1］，设φ：C2→C，且有φ（q（z），zq′（z））＝h（z）．若L（z，t）＝φ（q（z），tzq′（z））是一个从属链且p∈H［a，1］∩Q，则h（z）≺φ（p（z），zp′（z））表明q（z）≺p（z）．

在试验示范的跟踪过程中，云天化产品示范田的桃长势旺盛，中期表现出挂果多，果实品相好，桃树枝干健壮；采收期桃色泽好，果形均匀，畸形果少，口感佳。示范田施用肥料总量75kg、对照田肥料总量115kg。示范田少用40kg肥料投入的成本按照市场价格结算，示范田500元、对照田600元，化肥投入成本同比下降100元。,示范田亩增产 240kg，亩增收415.6元，给农户带来的一定的经济效益。通过试验示范，云天化四全水溶系列、镁立硼系列肥料得到了种植户的认可。

引理5［10］921设p∈Q，p（0）＝a，q（z）＝a＋anzn＋…在U 内解析并且q（z）≠a，n≥1．若q不从属于p，则存在这里使得

2 主要结论

定理1设f，g∈Ap．假设

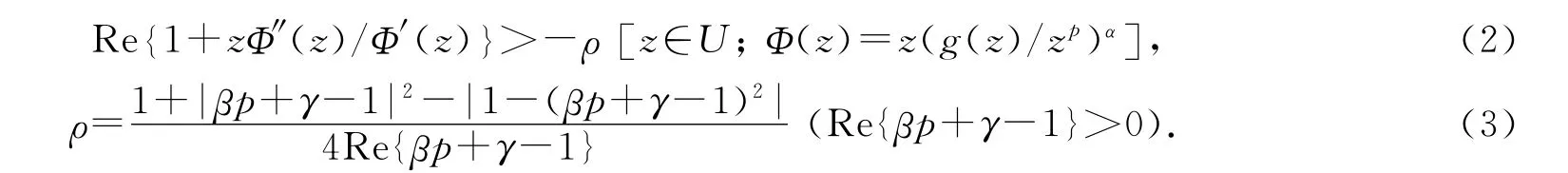
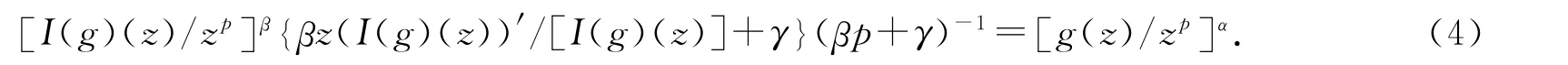
对G（z）取对数后求导，得

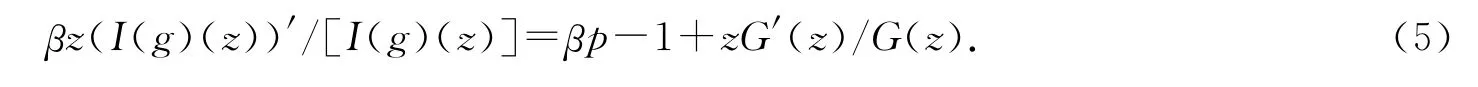
由（4），（5）式得

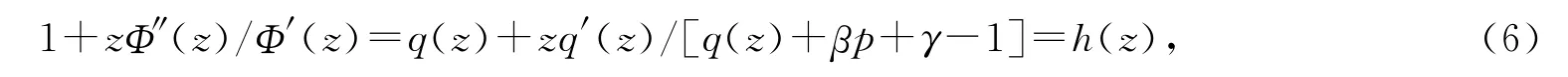
由（2）式可得Re｛h（z）＋βp＋γ－1｝＞0（z∈U）．利用引理2，可知微分方程（6）有一个解q∈H，q（0）＝h（0）＝1．设

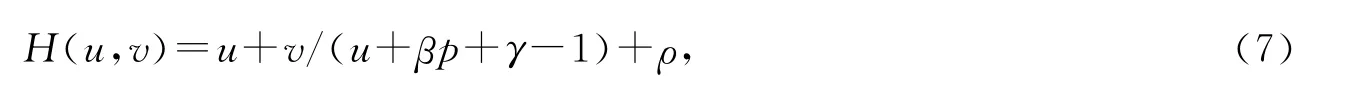
然后证明Re｛H（i s，t）｝≤0，s∈R，t≤－（1＋s2）／2．由（7）式有

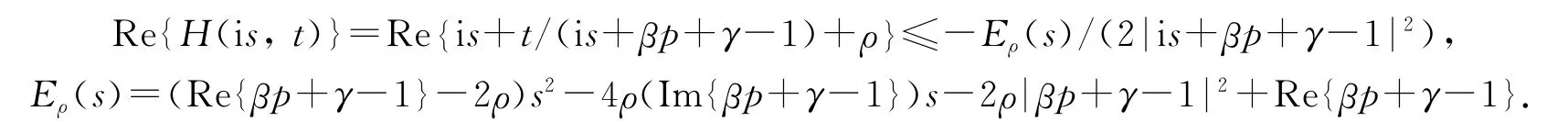
因为Eρ（s）中s2的系数大于等于0，而且可以验证Eρ（s）是关于s的完全平方，因此Re｛H（i s，t）｝≤0利用引理1，有Re｛q（z）｝＞0，即G（z）是凸单叶的．

最后证明F（z）≺G（z）．不失一般性，可以假设G 在¯U 上是单叶解析函数，并且

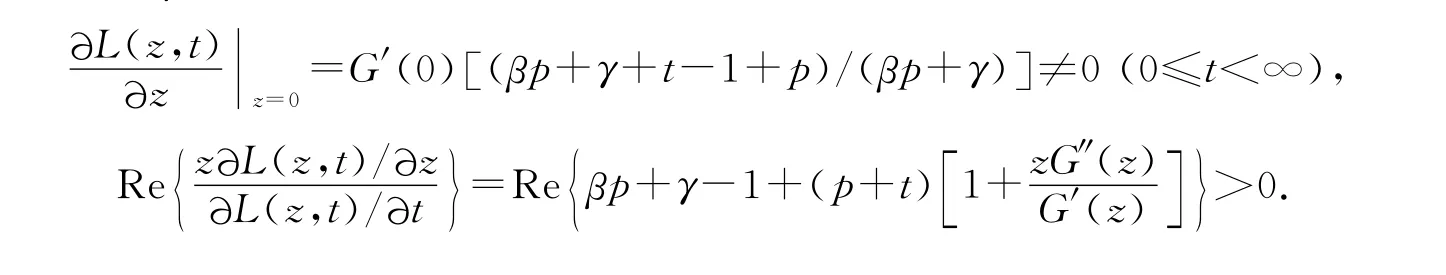
利用引理5，可知L（z，t）是从属链．由从属链的定义可知现假设F 不从属于G，利用引理5，存在点满足因此，此结论与矛盾．定理1得证．

定理2设f，g∈Ap．假设

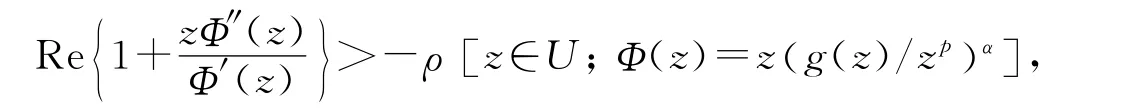
结合定理1和定理2可以得到以下sandwich－type定理．

定理3设f，gk∈Ap（k＝1，2）．假设满足

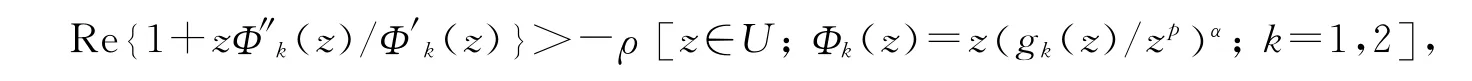
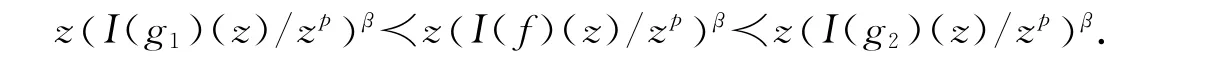
［1］ LIU Jinlin，OWA S．Properties of certain integral operator［J］．Int J Math Math Sci，2004，3（1）：351－359．

［2］ 施冬芳，鲁大前，王敏．由Noor积分算子定义的解析函数的性质［J］．扬州大学学报：自然科学版，2008，11（1）：1－4．

［3］ ALI R M，NAGPAL S，RAVICHANDRAN V．Second－order differential subordination for analytic functions with fixed initial coefficient［J］．Bull Malays Math Sci Soc，2011，34（3）：611－629．

［4］ MILLER S S，MOCANU P T．Differential subordinations and univalent functions［J］．Michigan J Math，1981，28（2）：157－172．

［5］ BULBOACǍT．Classes of first－order differential superordinations［J］．Demonstr Math，2002，35（2）：287－292．

［6］ BULBOACǍ T．A class of superordination－preserving integral operators［J］．Indag Math：New Ser，2002，13（3）：301－311．

［7］ ALI R M，RAVICHANDRAN V，SEENIVASAGAN N．On subordination and superordination of the multiplier transformation for meromorphic functions［J］．Bull Malays Math Sci Soc，2010，33（2）：311－324．

［8］ AOUF M K，SEOUDY T M．Sandwich theorems for higher－order derivatives of p－valent functions defined by certain linear operator［J］．Bull Korean Math Soc，2011，48（3）：627－636．

［9］ SHANMUGAM T N，JEYARAMAN M P．On sandwich theorems for certain subclasses of analytic functions associated with Dziok－Srivastava operator［J］．Taiwan J Math，2009，13（6B）：1949－1961．

［10］ CHO N E，KIM I H，SRIVASTAVA H M．Sandwich－type theorems for multivalent functions associated with the Srivastava－Attiya operator［J］．Appl Math Comput，2010，217（2）：918－928．

［11］ CHO N E，KWON O S．A class of integral operators preserving subordination and superordination［J］．Bull Malays Math Sci Soc，2010，33（3）：429－437．