带分布型时滞的分数阶脉冲控制系统的能控性
胡 宏,朱 彦
(1.徐州工程学院 数理学院,江苏 徐州221008;2.安徽大学 数学科学学院,合肥230039)
近年来,分数阶微积分学理论及其应用发展迅猛[1-4],而分数阶控制系统也吸引了诸多学者的关注[3-10].实际控制系统中普遍存在时滞现象,而时滞往往会导致控制系统性能的完全改变,因此时滞系统的控制一直是研究的热点问题[3-5].BALACHANDRAN[4]曾研究了一类带分布型时滞的分数阶控制系统的能控性;最近,GUO[3]又讨论了脉冲分数阶时变系统的能控性.本文在上述研究的基础上,拟探讨带分布型时滞的分数阶脉冲控制系统的能控性问题.考虑下列带分布型时滞的分数阶脉冲控制系统,其状态方程为
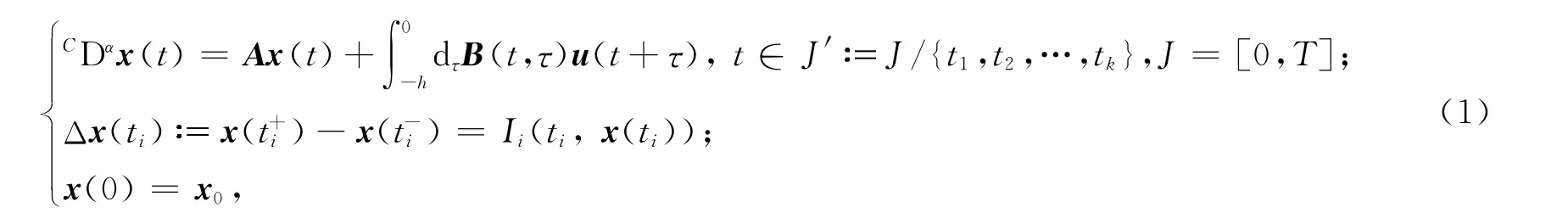
其中0<α<1,CDα是一个标准的Caputo型微分(具体定义将在下文中给出),状态x∈Rn,第2项积分是关于τ的Lebesgue-Stieltjes积分.给定h>0,对于函数u:[-h,T]→Rm及t∈J,用ut表示[-h,0]上的一个函数,且定义为ut(s)=u(t+s),s∈[-h,0).A 为n×n矩阵,B(t,τ)是n×m 维矩阵且满足以下3个条件:①对于固定的τ,其每一项关于t是连续的;②对于每一个t∈J,它在[-h,0]上关于τ是有界变差的;③它在(-h,0)上关于τ是左连续的.
1 预备知识
定义1[1]79函数f:[0,+∞)→R 的γ >0 阶Riemann-Liouville分数阶积分为Iγ0+f(t)=其中Γ(·)为gamma函数,右边是在[0,∞)上逐点定义的.
定义2[1]80函数f:[0,+∞)→R 的γ>0阶Riemann-Liouville分数阶微分为
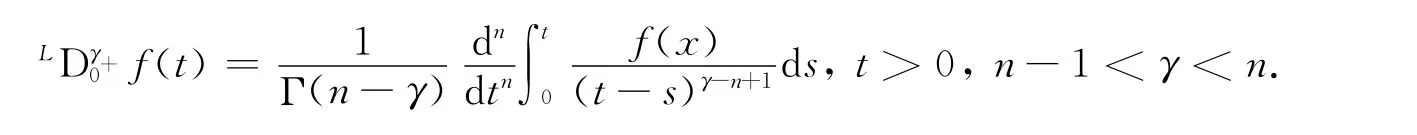
定义3[1]91函数f:[0,+∞)→R 的γ>0阶Caputo分数阶微分为
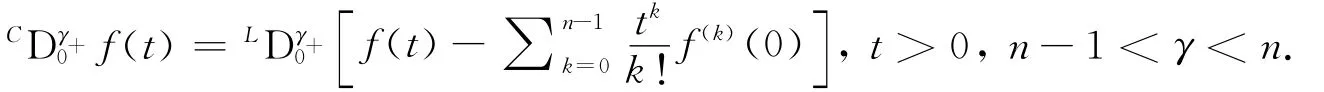
注11)若f(t)∈Cn[0,∞),则C
2)常数的Caputo导数恒为0.
定义4[1]42含两参数的Mittag-Leffler函数定义为其中α>0,β>0,C表示复数域.
注21)当β=1时,
2)当β =1 时,上 述 提 及 的Mittag-Leffler 函 数 的 矩 阵 拓 展 形 式 可 表 示 为Eα(Atα)=
根据文献[2-4],可以得到方程(1)的解为
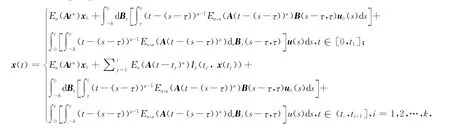
2 主要结论
定义5称系统(1)在[0,tf](tf∈(0,T])上为状态能控,是指给定任意两个状态x0,xtf∈Rn,存在一个控制u(t):[0,tf]→Rm,使得(1)的解满足x(tf)=xtf.
为方便起见,现引入如下记号:
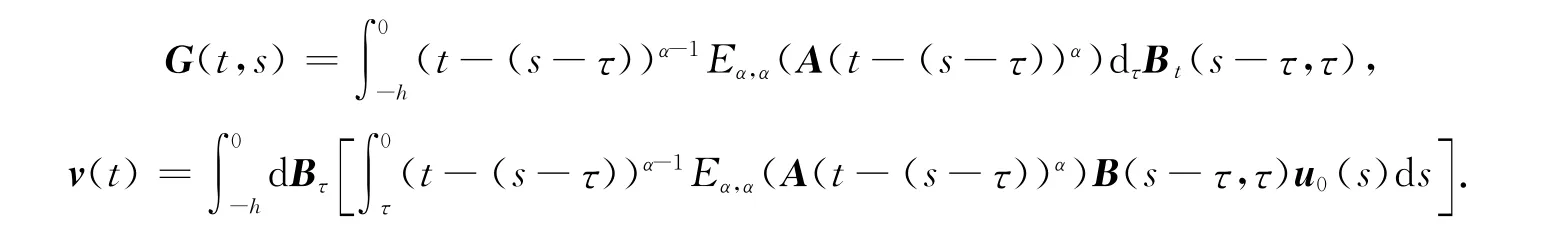
定理1系统(1)在[0,tf]上能控的充分必要条件是:存在时刻tf>0,使如下定义的格拉姆矩阵为非奇异.
证明 先证充分性.已知Wc[0,tf]非奇异,须证系统能控.采用构造性方法,由Wc[0,tf]非奇异,可知存在对状态空间中的任一非零状态x0,可构造相应控制输入为
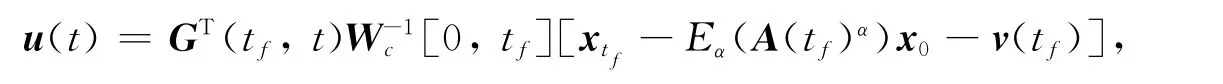
使得u(t)作用下状态x(t)在时刻tf的结果为
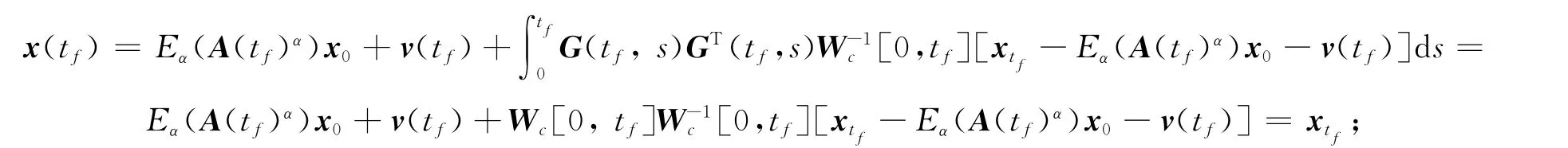
因此,当tf∈[0,t1]时,系统(1)在[0,tf]上能控.
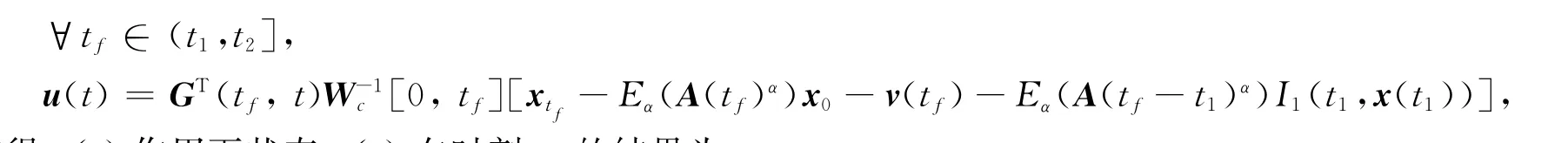
使得u(t)作用下状态x(t)在时刻tf的结果为
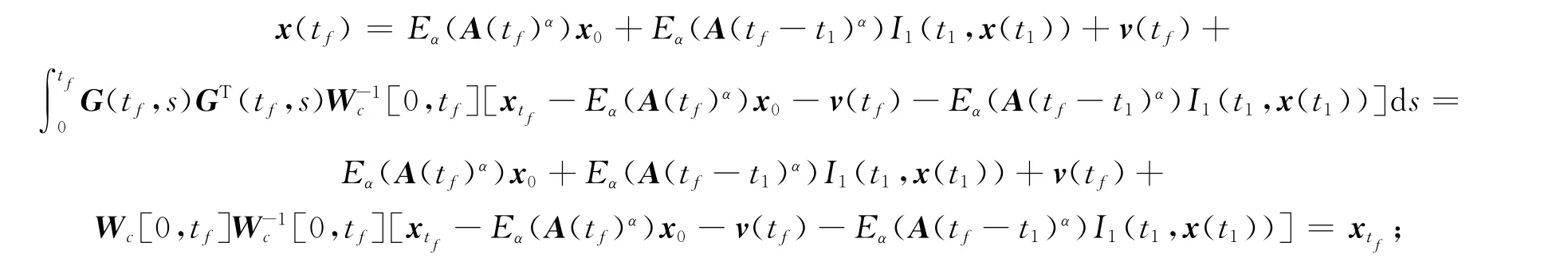
因此,当tf∈(t1,t2]时,系统(1)在[0,tf]上能控.更一般地,使得u(t)作用下状态x(t)在时刻tf的结果为
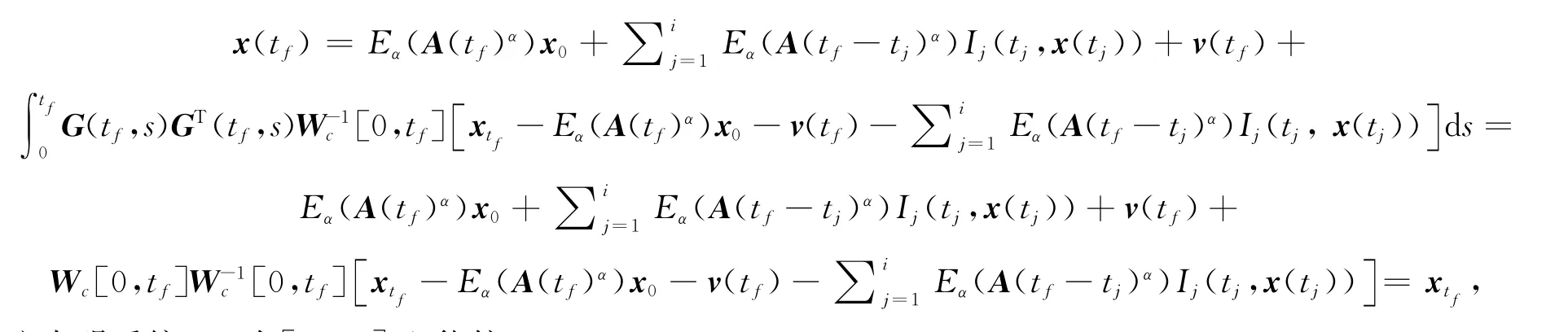
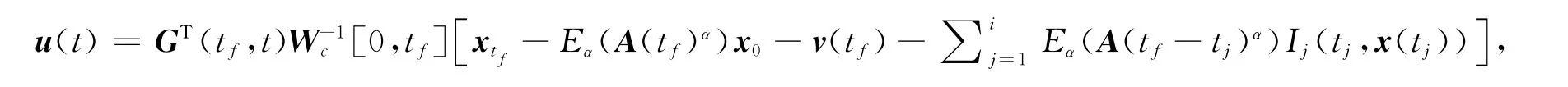
这表明系统(1)在[0,tf]上能控.
再证必要性.已知系统(1)能控,须证Wc[0,tf]非奇异.采用反证法,反设Wc[0,tf]奇异,不失一般性,∀tf∈(ti,ti+1],存在一个非零状态y,使得yTWc[0,tf]y =0,即s)yds=0,于是yTG(tf,s)=0,s∈[0,tf].取
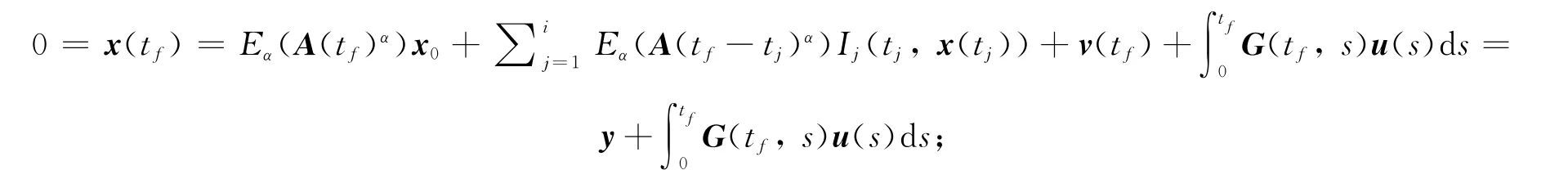
3 举例
考虑下面的分布型时滞的分数阶脉冲线性控制系统:
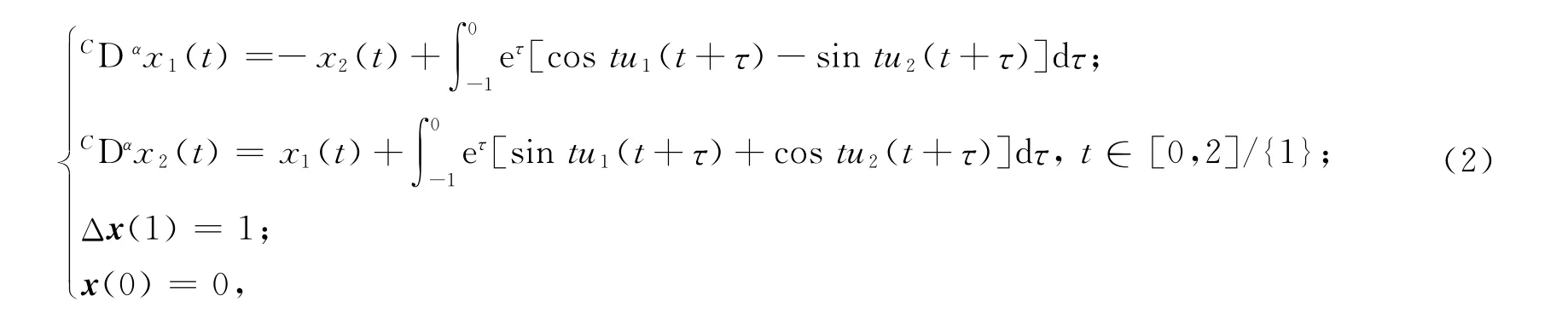
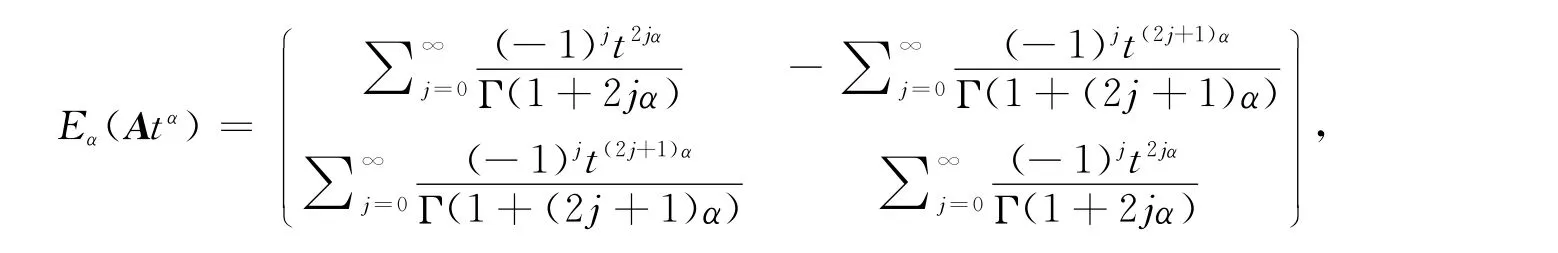
从而有
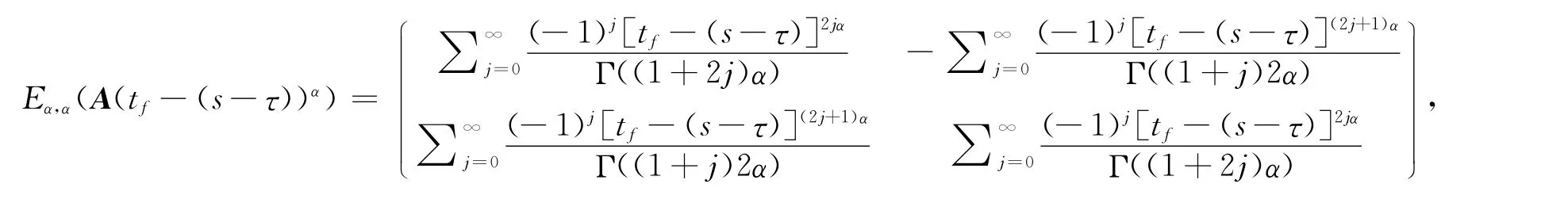
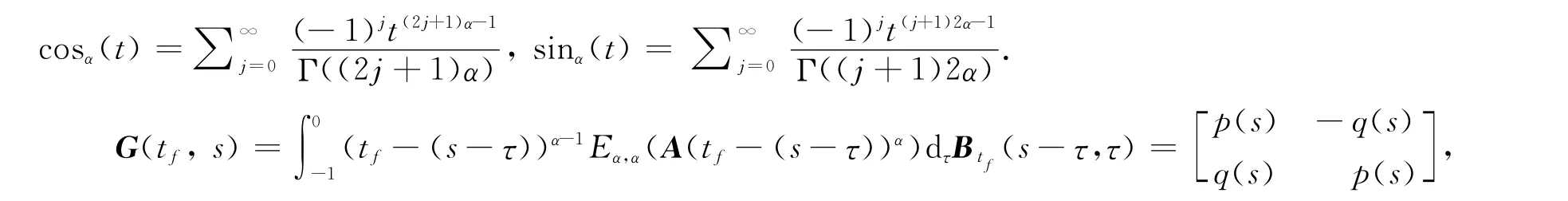
其中
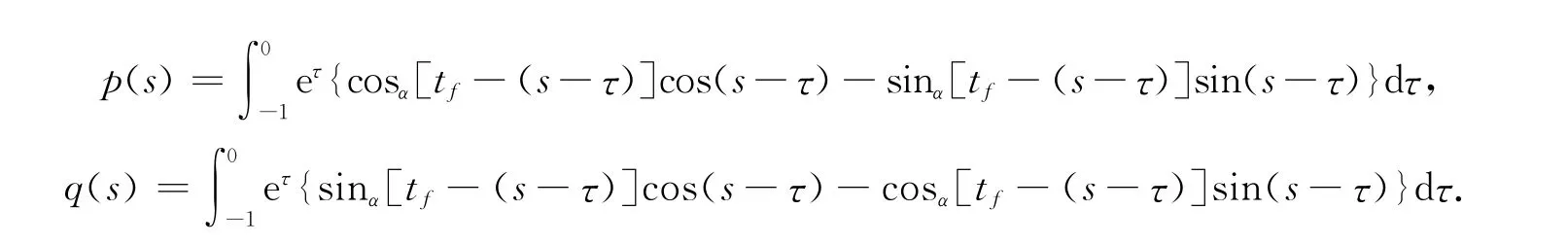
通过简单的矩阵计算,对tf>0,有
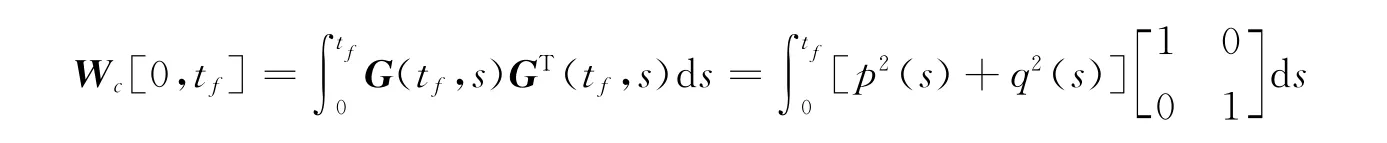
是非奇异的;因此,由定理1知,系统(2)在[0,tf]上可控.
[1] KILBAS A A,SRIVASTAVA H M,TRUJILLO J J.Theory and applications of fractional differential equations[M]//VAN MILL J.North-Holland Mathematics Studies,204.Amsterdam:Elsevier,2006:18-99.
[2] WANG Jinrong,FEKAN M,ZHOU Yong.On the concept new of solutions and existence results for impulsive fractional evolution equations[J].Dynamics of PDE,2011,8(4):345-361.
[3] GUO Tianliang.Controllability and observability of impulsive fractional linear time-invariant system [J].Comput Math Appl,2012,64(10):3171-3182.
[4] BALACHANDRAN K,ZHOU Yong,KOKILA J.Relative controllability of fractional dynamical systems with distributed delays in control[J].Comput Math Appl,2012,64(10):3201-3209.
[5] 朱清,盛朗,吕敏虎,等.一类非线性时滞系统的自适应动态面控制[J].扬州大学学报:自然科学版,2012,15(2):56-59.
[6] BALACHANDRAN K,PARK J Y,TRUJILLO J J.Controllability of nonlinear fractional dynamical systems[J].Nonlinear Anal:Theory,Methods &Appl,2012,75(4):1919-1926.
[7] GUAN Zhihong,QIAN Tonghui,YU Xinghuo.On controllability and observability for a class of impulsive systems[J].Syst Control Lett,2002,47(3):247-257.
[8] XIE Guangming,WANG Long.Controllability and observability of a class of linear impulsive systems[J].J Math Anal Appl,2005,304(1):336-355.
[9] JOURANI A.Controllability and strong controllability of differential inclusions[J].Nonlinear Anal:Theory,Methods &Appl,2012,75(3):1374-1384.
[10] 郑大钟.线性系统理论[M].2版.北京:清华大学出版社,2002:135-208.

