具复杂偏差变元的一类Liénard方程周期解

陈月红

（广东技术师范学院 计算机学院，广州510665）

近年来，有关Duffing型方程和Liénard型方程方面的研究成果［1－4］已有很多，且因为其在经济学、生态学、控制论等方面的广泛应用而逐渐成为热点．相对而言，关于具复杂偏差变元的时滞Liénard型方程的研究尚不多见．2003年，李鹏程［5］研究了含偏差变元的时滞Duffing型微分方程周期解的存在性．2004年，葛渭高［6］研究了含偏差变元的Liénard型微分方程．作为Liénard方程的特殊形式，笔者［7］曾探讨了含复杂偏差变元的时滞非自治Duffing型微分方程周期解的存在性．在上述工作的基础上，本文拟研究带复杂偏差变元的二阶Liénard型微分方程

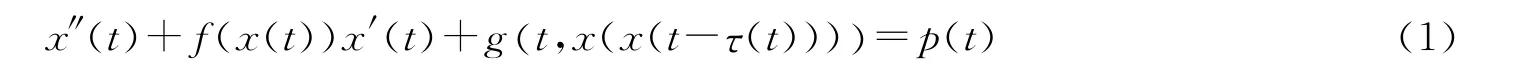
周期解的存在性问题．文中定理1是对文献［5］195定理2的推广，并且由于考虑的是具有复杂偏差变元的函数g（t，x），而非g（x）的情形，故定理1中所得方程（1）的周期解的存在性条件与时滞变量τ（t）的关系不同于文献［6］236中的相应结论．

1 预备知识

设X，Y 均为Banach空间．L：DomL⊂X→Y 是线性映射，N：X→Y 是连续映射．若dim Ker L＝co dim ImL＜＋∞及ImL 在Y 中闭，则L 是指标为0的Fredholm 算子．设L 如前所述，则存在连续的投影算子P：X →X 与Q：Y →Y，使得Im P＝Ker L，Im L＝Ker Q＝Im（I－Q），从而L｜DomL∩KerP：（I－P）X→ImL 有逆映射Kp．若Ω 是X 中开有界集，当QN（¯Ω）有界且紧时，映射N 是¯Ω 上的L－紧集．又因ImQ 与Ker L 同构，故存在同构映射J：ImQ→Ker L．

引理1［1］26（Mawhin连续性定理） 令L 是指标为0的Fredholm 算子，N 是¯Ω 上的L－紧集，设

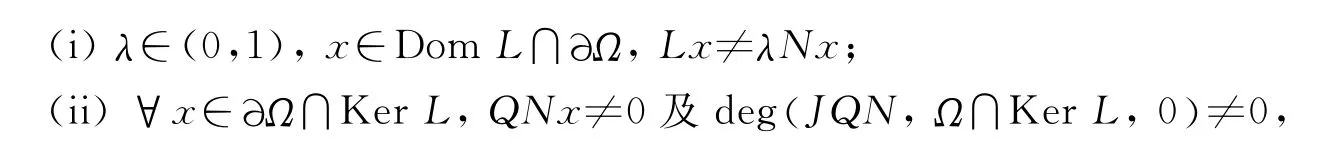
则方程Lx＝Nx 至少存在一个周期解，当∀x∈∂Ω∩DomL 时．

引理2［8］令CT是由实连续的T－周期泛函x＝x（t）构成的集合，则∀x＝x（t）∈C（1）（R，R）∩CT及∀ξ∈［0，T］，有

引理3［9］设x（t）∈CT，τ′（t）＜1，则

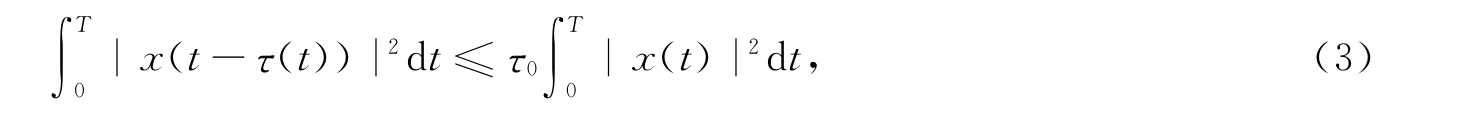
记X＝｛x｜x∈C（1）（R，R），x（t＋T）＝x（t），∀t∈R｝，其范数为‖x‖1＝max｛‖x‖0，‖x′‖0｝，其中‖x‖0＝maxt∈［0，T］｜x（t）｜．类似地，令Y＝｛y｜y∈C（R，R），y（t＋T）＝y（t），∀t∈R｝，范数为‖y‖0＝maxt∈［0，T］｜y（t）｜．易证X，Y 均为Banach空间．定义映射X∩C（2）（R，R）→Y，N：X→Y，并有Lx（t）＝x″（t），t∈R，非线性算子Nx（t）＝－f（x（t））x′（t）－g（t，x（x（t－τ（t））））＋p（t）．显然定义投影算子易验证Ker Q＝Im L＝Im（I－Q），Ker L＝ImP．L｜DomL∩KerP：（I－P）X→ImL 有一个定义在Kp上的逆映射，且映射L 是指标为0的Fredholm 算子［10］99．设Ω 是X 中开有界集，则映射N 是¯Ω 上的L－紧集［10］99－100．

2 主要结论

定理1设k，c，D＞0及以下条件成立：

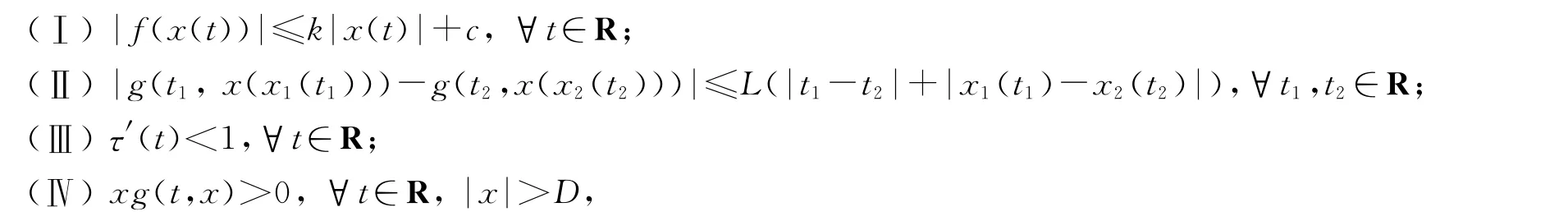
证明 先设方程

再令x（t）∈CT是方程（1）的任意T－周期解．将x（t）代入方程（4）中，并对方程两边从0到T 积分，得到据积分中值定理，∃ξ∈［0，T］，使得g（ξ，x（x（ξ－τ（ξ））））＝0．由条件（Ⅳ），得｜x（x（ξ－τ（ξ）））｜≤D．因｜x（ξ－τ（ξ））｜∈R，故∃t1∈［0，T］，使得｜x（t1）｜＝｜x（x（ξ－τ（ξ）））｜≤D．由（3）式及Hölder不等式，得

由（5）式，对t从0到T 积分，得

再对（5）式两边平方，得

对上式中的t从0到T 积分，得

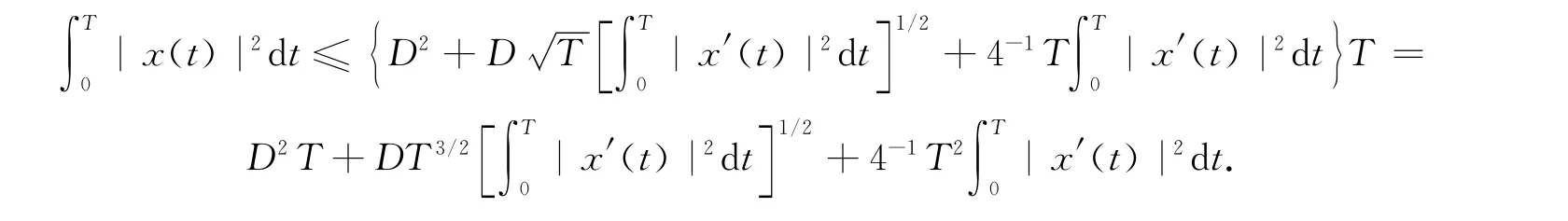
另一方面，

在（4）式两边同时乘以x（t），将方程两边对t从0到T 积分，得由此式和（3），（6）式，并应用Hölder不等式，得

其中｜p｜0＝maxt∈［0，T］｜p（t）｜．另外还可得到

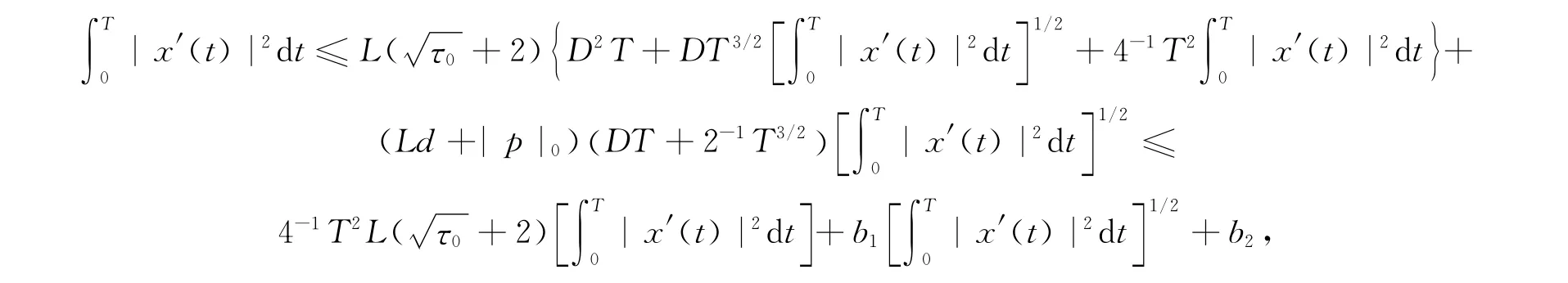
其中b1，b2＞0．因故存在a＞0，使得b2；从而存在与x 无关的常数M0＞0，使得

于是存在M1＞0，使得

以及存在M2＞0，使得

另外，因x（0）＝x（T），故存在t0∈［0，T］，使得x′（t0）＝0．将方程（4）两边从t0到t积分，得所以｜x′（t）｜≤由条件（Ⅰ），（6），（7），（8）式，结合Hölder不等式，对任意t∈［0，T］，有

即存在M3＞0，使得

又由（2），（7）式得

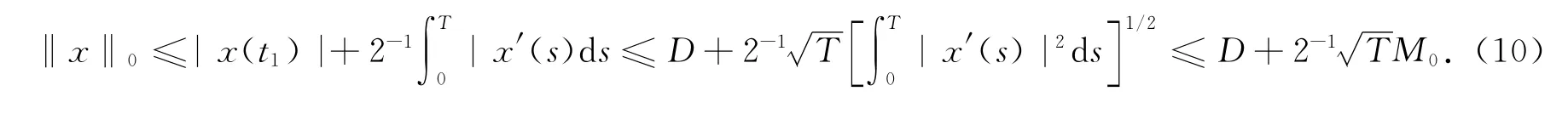
注定理1的条件（Ⅰ）改为（Ⅰ′）：｜f（x（t））｜≤k，∀t∈R，或者将条件（Ⅳ）改为（Ⅳ′）：xg（t，x）＜0，∀t∈R，｜x｜＞D，定理1的结论仍成立．

例1考虑方程其中于是取则易见定理1中条件（Ⅰ）～（Ⅳ）均满足，故由定理1知该方程至少有一个2－1－周期解．

［1］ GAINES R E，MAWHIN J L．Coincidence degree and nonlinear differential equations［M］／／Lecture Notes in Mathematics．Berlin：Springer，1977：26－43．

［2］ 王亚民，刘玉荣．时滞的周期神经网络模型周期解的存在性［J］．扬州大学学报：自然科学版，2005，8（4）：12－15．

［3］ 黄先开，向子贵．具有时滞的Duffing型方程x″＋g（x（t－τ））＝p（t）的2π周期解［J］．科学通报，1994，39（3）：201－203．

［4］ WANG Genqiang，CHENG Suisun．A priori bounds for periodic solutions of a delay Rayleigh equation［J］．Appl Math Lett，1999，12（1）：41－44．

［5］ 李鹏程．一类Duffing型时滞微分方程的周期解［J］．四川大学学报：自然科学版，2003，40（2）：195－198．

［6］ GE Weigao．On the existence of periodic solutions for a kind of Liénard equation with a deviating argument［J］．J Math Anal Appl，2004，289（1）：241－243．

［7］ CHEN Yuehong，WANG Genqiang．Periodic solutions of nonautonomous delay Duffing equations with a complex deviating argument［J］．Far East J Appl Math，2007，26（2）：159－170．

［8］ LI Jingwen，WANG Genqiang．Sharp inequalities for periodic functions［J］．Appl Math E－Notes，2005，5（1）：75－83．

［9］ WANG Zhengxin，QIAN Longxia，LU Shiping，et al．The existence and uniqueness of periodic solutions for a kind of Duffing－type equation with two deviating arguments［J］．Nonlinear Anal：Theory，Methods ＆ Appl，2010，73（9）：3034－3043．

［10］ CHEN Yuehong，LIN Weiwei．Existence of periodic solutions of iterative differential equations with deviating arguments［J］．Far East J Math Sci，2011，50（1）：95－104．