一类随机脉冲神经网络的聚类同步

李 朕，王 晶，徐 玲

（扬州大学 数学科学学院，江苏 扬州225002）

近年来，关于含有脉冲行为的神经网络的研究已引起国内外学者的广泛关注，而各种含有脉冲的神经网络动力学行为如同步性、稳定性等也是人们探讨的热门课题［1－3］．神经网络在信号传输中一般会产生时滞并受到其他随机波动而引起噪声，所以真实的神经网络应该是一个随机的动力系统［4－5］．然而，目前大多数对脉冲神经系统聚类同步的研究都集中于确定性系统，而有关随机脉冲网络的聚类同步研究报道较少［6－8］．在本文中，笔者拟讨论具有分布时滞及扰动的随机脉冲神经网络的指数聚类同步问题．文中Rn表示n 维欧式空间，Rn×m表示所有n×m 实矩阵构成的集合；对于实对称矩阵X 和Y，X≥Y（X＞Y）表示X－Y 是半正定的（正定的）；In是所有n 阶单位矩阵；｜·｜表示Rn中的欧式向量范数；E｛·｝表示数学期望算子；⊗为Kronecker积运算符；若A 是一个矩阵，则其中λmax（ATA）表示矩阵ATA 的谱半径．用‖A‖表示它的算子范数，

1 问题的提出

考虑在脉冲发生情况下同时具有混合时滞的随机神经网络系统：

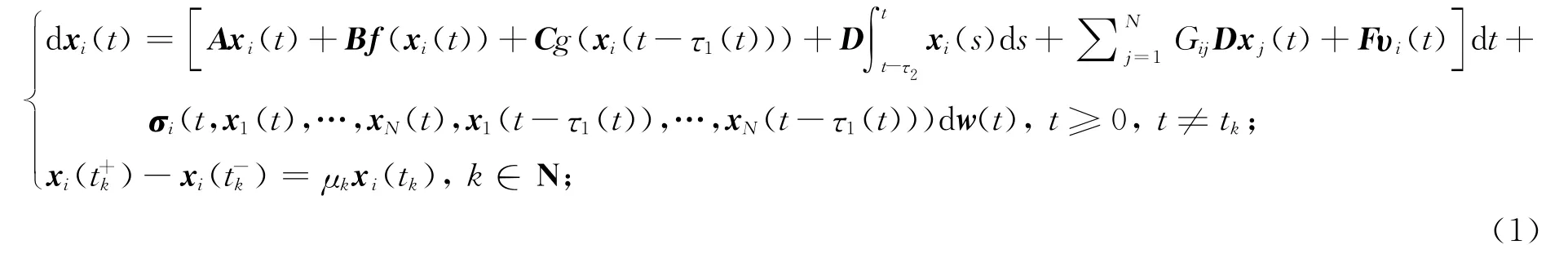
输出：

其中xi＝（xi1（t），xi2（t），…，xin（t））T∈Rn是神经网络的状态向量；A＝－diag｛a1，…，an｝且ai＞0；B，C，D 分别表示连接权矩阵、时滞连接权矩阵、内连接矩阵；G＝（Gij）N×N是网络的耦合矩阵；常数μk表示脉冲扰动强度；τ1（t）为时变的离散时滞，满足0≤τ1（t）≤τ＊1；τ2＞0为分布时滞；υi（t）∈L2［0，＋∞］是输入扰动；w（t）＝［w1（t），…，wn（t）］T是定义在完备概率空间（Ω，F，｛Ft｝t≥0，P）上具有自然滤波｛Ft｝t≥0的n维Brownian运动；f（xi（t））＝［f1（xi1（t）），…，fn（xin（t））］T和g（xi（t））＝［g1（xi1（t）），…，gn（xin（t））］T是单调递增的函数；F 是输入矩阵；U 为输出矩阵．

注1序列｛t1，t2，t3，…｝是一列严格增的离散脉冲时刻，xi（t）是左连续，即x（tk）＝x（t－k）；这样，系统（1）的解是一系列分段的左连续函数，其中不连续点为t＝tk，k∈N．初始函数为xi（s）＝φi（s），s∈［t0－τ1，t0］，i＝1，…，N，其中φi（·）＝［φi1（·），…，φiN（·）］T∈C（［t0－τ1，t0］，Rn）．

为了简化研究，同时又不失一般性，现给出如下假设．

假设1∀a，b∈R（a≠b），∃ls＞0，ks＞0（s＝1，2，…，n），使得函数fs（x（t））和gs（x（t））满足0≤（fs（a）－fs（b））／（a－b）≤ls，0≤（gs（a）－gs（b））／（a－b）≤ks．

假设2耦合矩阵其中Nij的所有行都相同，Nii∈Rmi×mi，Nij∈Rmi×mj，i，j＝1，2，…，k，如Nij＝（u，…，u）T，向量u＝（u1，…，umj）T．

假设3对于函数σ：R＋×Rn×Rn→Rn，存在常数ρ1＞0和ρ2＞0，满足σT（t，x，y）σ（t，x，y）≤ρ1xTx＋ρ2yTy．

2 预备知识

定义1 当υi（t）＝0时，如果存在β＞0，T＞0，M0＞0，将网络中的N 个节点分成k 个聚类，如｛（1，2，…，m1），（m1＋1，m1＋2，…，m1＋m2），…，（m1＋m2＋…＋mk－1＋1，…，m1＋m2＋…＋mk－1＋mk），m1＋m2＋…＋mk＝N｝，使得当t＞T 时都有E‖ξi（t；s）－ξj（t；s）‖≤M0e－βtsup－τ≤s≤0E‖ξi（s）－ξj（s）‖（其中ξi，ξj在同一聚类中），则系统（1）称为全局指数聚类同步，β为系统的衰减率，M0为系统的衰减系数．

定义2当υ（t）＝0时，系统（1）全局指数聚类同步，并在系统（1）的初始函数恒为0时，有

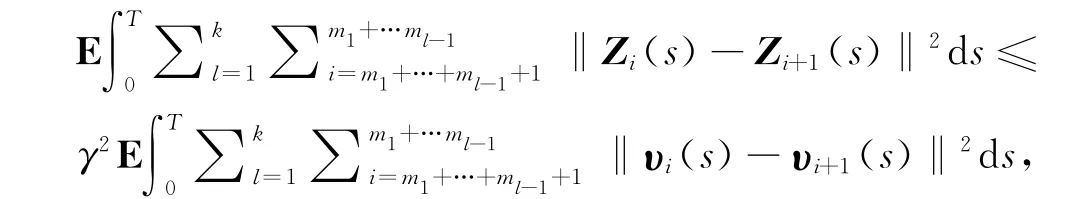
则称系统（1）为带有衰减水平γ的指数聚类同步，其中∀T＞0，υi（t）为非零输入扰动．

注2本文中的定义1与定义2是对文献［7］3中定义3与定义4在随机系统中的推广．

引理1［9］336在假设2成立的前提下，N－k阶方阵~H 满足~MG＝~H~M，其中

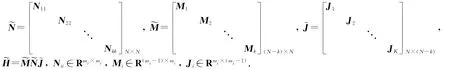
注3矩阵Mi和Ji的含义见文献［9］336和文献［10］．

引理2［11］设向量函数ω：［0，r］→Rm，对于任意的对称矩阵W∈Rm×m和标量r＞0，有

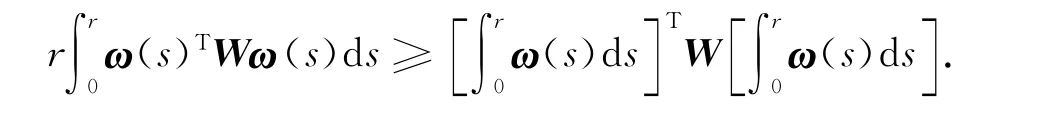
3 主要结论及其证明

利用Kronecker积的性质，定义＾M＝~M⊗In，可以将系统（1）重写为

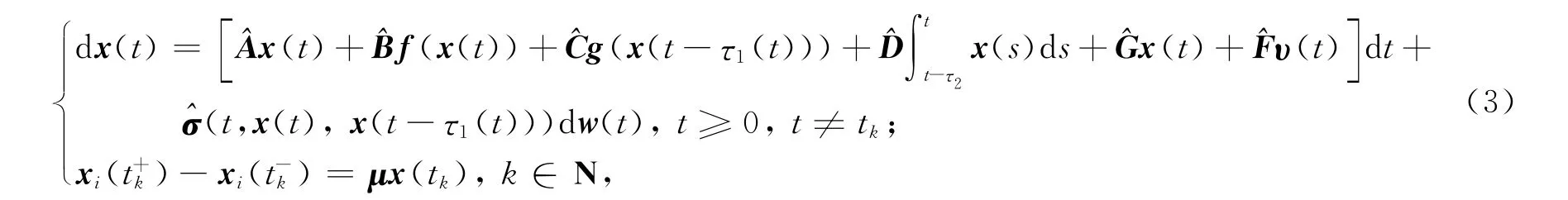
为了证明主要结论，须要定义A1＝IN－k⊗A，B1＝IN－k⊗B，C1＝IN－k⊗C，D1＝IN－k⊗D，F1＝

定理1称满足假设1～3的系统（3）是带有衰减水平γ的指数聚类同步的．如果存在3个正定矩阵，Pi＞0，Pi∈R（N－k）n×（N－k）n（i＝1，2，3），2 个 正 定 对 角 矩 阵Λ ＝diag｛Λ1，…，Λ（N－k）n｝∈R（N－k）n×（N－k）n和Γ＝diag｛Γ1，…，Γ（N－k）n｝∈R（N－k）n×（N－k）n，使得－2≤μk≤0，β＞0，并有下列LMIs成立：

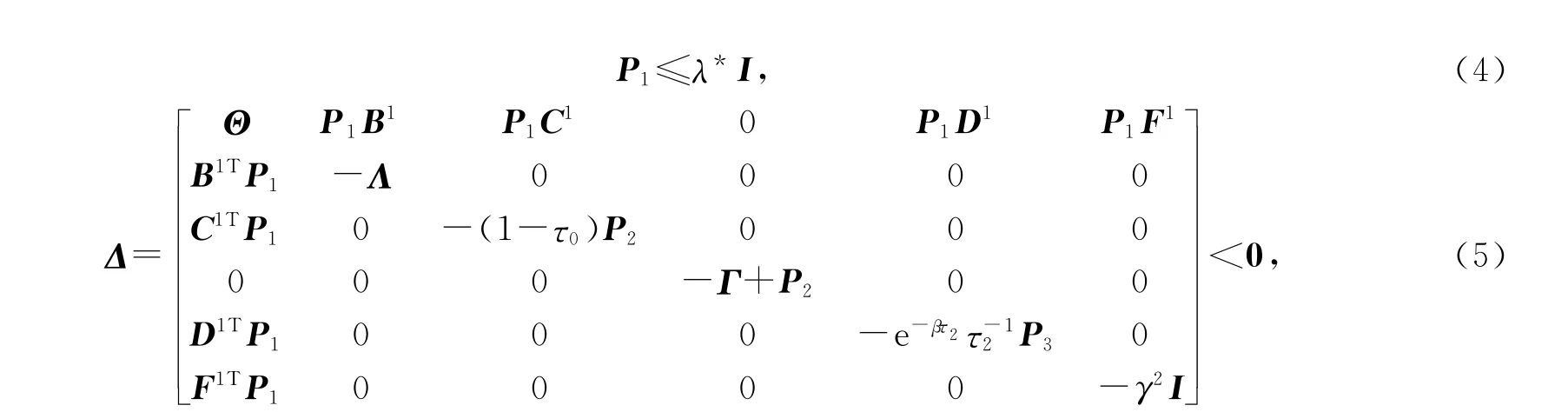
其中Θ＝βP1＋P1A1＋A1TP1＋P1＾H＋＾HTP1＋（1－e－βτ2）β－1P3＋＾LΛ＾L＋＾KΓ＾K＋U1TU1＋［ρ1＋ρ2（1－τ0）－1］λ＊I，λ＊＞λmax（P1），U1＝IN－k⊗U，τ1（t）为满足系统（1）的时变离散时滞，0≤τ1（t）≤τ＊1，由引理1定义．

证明 首先，证明在υ（t）＝0情况下随机的脉冲神经网络系统（3）是指数聚类同步的．由（5）式可知Δ＜0，所以有

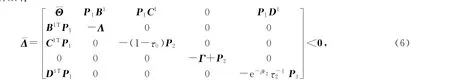
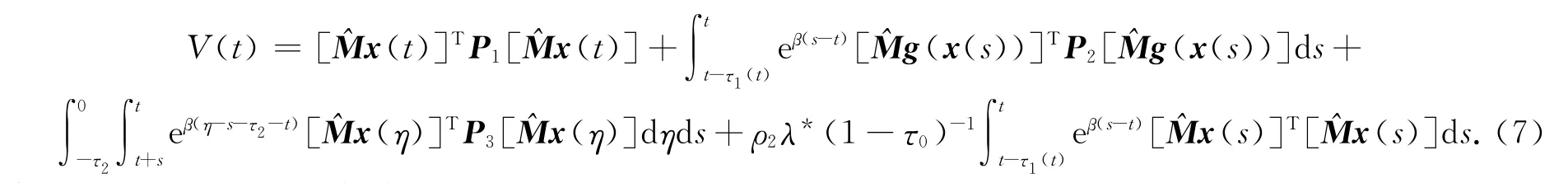
当t≠tk（k∈N）时，根据广义Itô公式可得

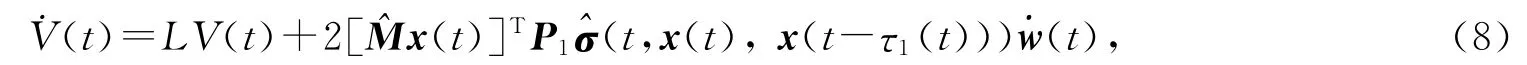
由假设1、假设3和引理3经过简单计算不难得到LV（t）＋βV（t）≤ηT¯Δη，因此

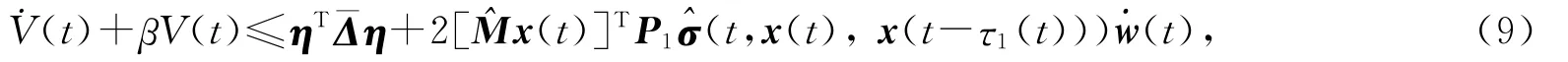
进一步地，当－2≤μk≤0，β＞0时，由不等式方程（9）有

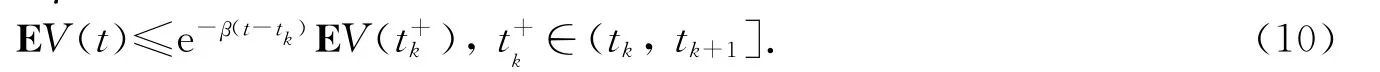
另一方面，由于xi（t＋k）－xi（t－k）＝μkxi（tk），通过计算可得V（t＋k）≤V（t－k），所以

设0＝t0＜t1＜…＜tk＜…（k∈N）表示在区间（0，t）内的脉冲发生时刻，则由不等式方程（10）与（11）式可知

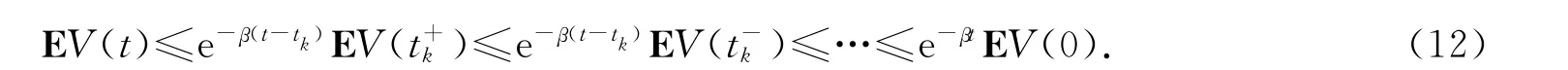
令M0＝εδ－1，由定义1可知，当υ（t）＝0时，系统（3）全局指数聚类同步．

其次，考虑在包含扰动υ 的情况下系统（3）是带有衰减水平的指数聚类同步的．令显然ψ（x）＜0，即Eψ（x）＜0，故，于是可得

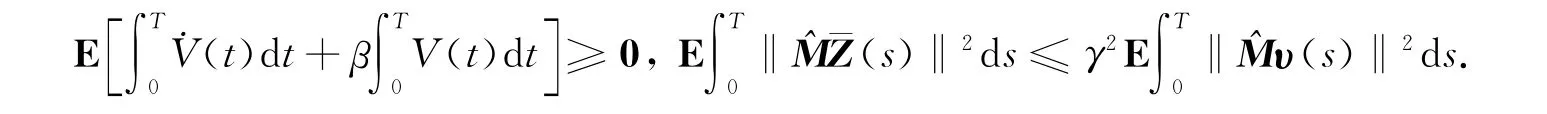
根据定义1和定义2，可以得到系统（3）是带有衰减水平的指数聚类同步的．

4 数值例子

现通过一个简单的例子来说明上述结果．考虑在两个细胞的神经网络（1）中，参数选取如下：

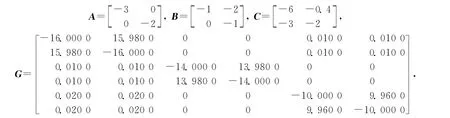
D＝I2，τ0＝τ2＝0．2，ρ1＝0．4，ρ2＝4，γ＝4，β＝0．6，f（x）＝g（x）＝0．1｜sin x｜，显然可得li＝ki＝0．1，故利用Matlab软件中的LMI得到可行解．

［1］ LU Jianquan，HO D W C，CAO Jinde．A unified synchronization criterion for impulsive dynamical networks［J］．Automatica，2010，46（7）：1215－1221．

［2］ WU Sichao，LI Chuandong，LIAO Xiaofeng，et al．Exponential stability of impulsive discrete systems with time delay and applications in stochastic neural networks：a Razumikhin approach［J］．Neurocomputing，2011，82：29－36．

［3］ 蒋国民，刘玉荣．基于线性矩阵不等式神经网络的鲁棒稳定性［J］．扬州大学学报：自然科学版，2006，9（4）：7－11．

［4］ LIU Yurong，WANG Zidong，LIU Xiaohui．Global exponential stability of generalized recurrent neural networks with discrete and distributed delays［J］．Neural Networks，2006，19（5）：667－675．

［5］ LIU Yurong，WANG Zidong，LIU Xiaohui．On global exponential stability of generalized stochastic neural networks with mixed time－delays［J］．Neurocomputing，2006，70（1／3）：314－326．

［6］ LU Jianquan，HO D W C，CAO Jinde，et al．Exponential synchronization of linearly coupled neural networks with impulsive disturbances［J］．IEEE Trans on Neural Networks，2011，22（2）：329－335．

［7］ ZHANG Wenbing，TANG Yang，FANG Jian’an，et al．Exponential cluster synchronization of impulsive delayed genetic oscillators with external disturbances［J］．Chaos，2011，21（4）：043137：1－12．

［8］ SHI Bingxiong，LU Junan，LYU Jinhu，et al．Adaptive and impulsive cluster synchronization of a general complex dynamical network［C］／／Proc ICNSC．Chicago，IL，USA：IEEE，2010：704－709．

［9］ CAO Jinde，LI Lulu．Cluster synchronization in an array of hybrid coupled neural networks with delay［J］．Neural Networks，2009，22（4）：335－342．

［10］ WU C W，CHUA L O．Synchronization in an array of linearly coupled dynamical systems［J］．IEEE Trans on Circuits ＆Systems－I：Fundam Theory ＆Appl，1995，42（8）：430－447．

［11］ GU Keqin，KHARITONOV V L，CHEN Jie．Stability of time－delay systems［M］．Boston：Birkhäuser，2003：277．