室内初始温度较高条件下的瞬态自然通风

杨秀峰，钟 珂，亢燕铭，左 滨

（1．东华大学 环境科学与工程学院，上海201620；2．扬州大学 能源与动力工程学院，江苏 扬州225127）

室内热空气的浮升力驱动的热压自然通风是自然通风的一种基本形式．当室内有热源时，热源周围的空气被加热，形成向上浮升的热羽流，热羽流浮升力产生的烟囱效应使室外空气由下部通风口流入，室内热空气由上部通风口排出，室内逐渐形成竖向的空气密度分层［1－3］．热压自然通风经过一定时间的发展后将到达稳态，但是由于通风发展过程的复杂性，这方面的研究并不多见．KAYE等人［4］研究了室内外初始温度相同且室内地面有局部热源条件下热压自然通风的瞬态发展过程．FITZGERALD等人［5］研究了不同室内初始温度条件下房间底部的均匀分布热源驱动的瞬态热压通风．BOWER 等人［6］研究了当室内点热源强度增加或减小时热压通风由初始稳态向另一稳态过渡的瞬态过程．SANDBACH 等人［7］利用一个变形的filling－box模型描述了室内外初始温度相同条件下的瞬态通风过程．室内初始温度高于室外且室内有热源条件下的自然通风是一种常见的热压通风情形，如室内温度较高且有观众的报告厅的开窗通风，FITZGERALD 等人［8］利用简化的理论模型分析了该情形下瞬态通风过程的4种发展模式，本文针对其中一种典型模式，给出一个改进的理论模型，并结合实验数据分析改进模型的合理性，又利用该模型分析了瞬态热压通风过程中热分层状况和通风量随时间变化的规律．

1 室内初始温度较高条件下瞬态热压通风的典型模式

如果通风发展过程中热羽流的浮升力总是大于室内原有热空气的浮升力，则热羽流能够穿越室内原有热空气层浮升至天花板．同时，如果天花板处热羽流的流量大于房间的瞬时通风量，则部分热羽流由上部通风口排出，其余部分堆积在天花板处，形成温度高于室内原有热空气的热空气层；于是，通风过程中室内空间分为竖向的3个区域，即由下部通风口进入室内的冷空气层、室内原有热空气层及上部新形成的热空气层，如图1所示．图1中3层空气层之间的2个热分层界面的高度分别记为h1和h2，房间高度为H，Ta，T0，T 分别为3层空气层的温度，g′0和g′分别为室内原来热空气层和新形成热空气层的浮升力，q 为瞬时通风量．当通风发展至稳态时，室内原有热空气层消失，2个热分层界面重合，距地面的高度为hss，稳态通风量为qss．

通风过程中室内原有热空气与下部冷空气之间的分层界面向上移动，该分层界面处的热羽流浮升力g′p，h1逐渐减小，并最终趋于稳态值g′p，hss；因此，如果通风过程中热羽流的浮升力g′p，h1总是大于室内原有热空气的浮升力g′0，则必然有g′p，hss＞g′0．

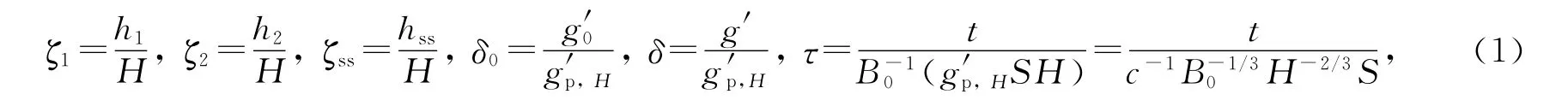
以热羽流首次浮升至天花板的时刻为通风过程的初始时刻，该时刻的房间通风量和天花板处热羽流的流量［3］1628，［8］2780分别为q＝A＊（g′0·H）1／2，qp，H＝cB01／3H5／3，其中A＊为有效通风面积，m2；c＝（6α／5）（18απ2／5）1／3为常数，α＝0．083为卷吸系数［9－10］；B0为热源的浮升力通量，m4·s－3．当初始时刻天花板处热羽流的流量qp，H大于房间通风量q 时，天花板处才会形成新的热空气层；因此，该通风模式的实现条件为g′p，hss＞g′0且qp，H＞q．

定义下列无量纲量：

式中g′p，H＝c－1B2／30H－5／3，为热羽流初次到达天花板时的浮升力，S 为房间面积．

2 瞬态热压通风过程的理论模型

2．1 Fitzgerald－Woods理论模型

Fitzgerald－Woods模型［8］2780（以下简称F－W 模型）将室内初始温度较高条件下热压通风过程的气流型式视为置换通风，假设通风过程中上部热空气层内温度均匀分布，并由此给出了该通风模式下室内不同区域的物理量守恒方程

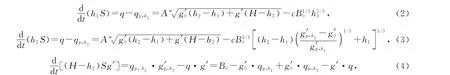
式中qp，h1和qp，h2分别为2个热分层界面处热羽流的流量，g′p，h1和g′p，h2分别为2个热分层界面处热羽流的浮升力．以热羽流首次到达天花板时为初始时刻，则初始条件为h1＝0，h2＝H，g′＝g′0＋g′p，H．

2．2 改进的模型

通风过程中热羽流依次穿过下部冷空气层、室内原有热空气层和上部热空气层后到达天花板并向周围扩散，进而在天花板下方形成一空气薄层，该空气薄层的温度和浮升力分别大于其下方热空气层的温度和浮升力；于是，通风过程中可以将室内空间视为由竖向的4个区域组成，由下向上依次是流入的室外冷空气层、室内原有热空气层、新形成的热空气层以及紧靠天花板的热空气薄层．4层空气层之间存在着3个热分层界面，其距地面的高度分别记为h1，h2，hc．该情形下室内热分层状况的发展过程如图2所示，图中Tc和g′c分别为天花板处热空气薄层的温度和浮升力．

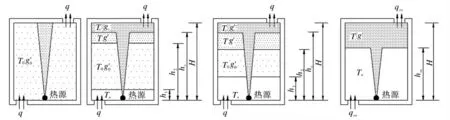
图2 改进模型的空间热分层示意图Fig．2 Schematic diagram of the thermal stratification of the modified model

通风过程的瞬态通风量q为A＊［g′0（h2－h1）＋g′（hc－h2）＋g′c（H－hc）］1／2．参照文献［8］2781中热羽流在多层空气层内浮升的流量表达式，将热羽流穿过冷空气层、室内原有热空气层和新形成热空气层后到达天花板处的流量qp，H，new（区别于热羽流穿过单一空气层到达天花板时的流量qp，H）表示为

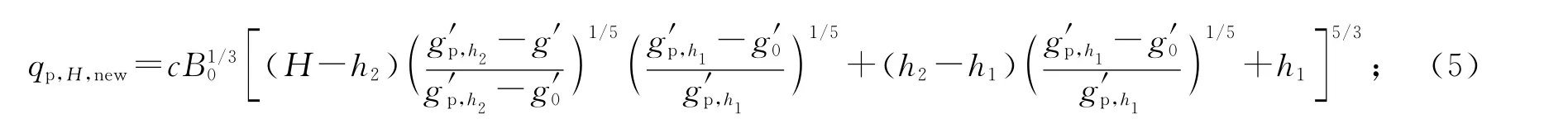
热羽流穿过多层空气层后浮升至天花板处的浮升力g′p，H，new为

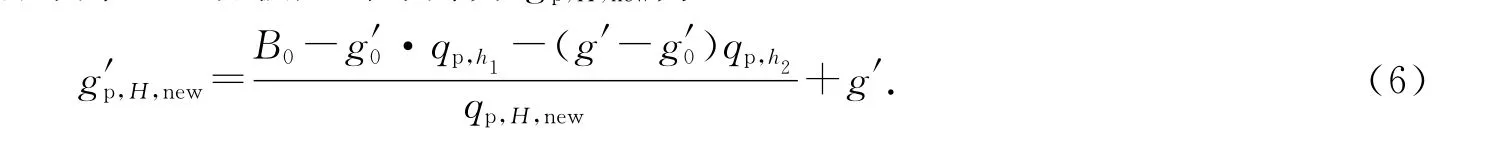
参照文献［10］876中热羽流穿过单一空气层到达天花板后扩散形成的热空气层的厚度表达式，将热羽流穿过多层空气层到达天花板后扩散形成的热空气薄层的厚度表示为

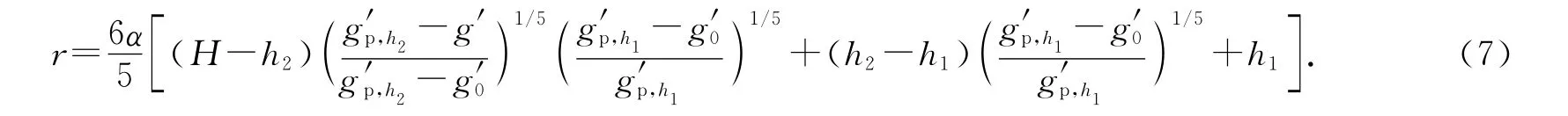
天花板处热空气薄层距离地面的高度为hc＝H－r，其无量纲形式为

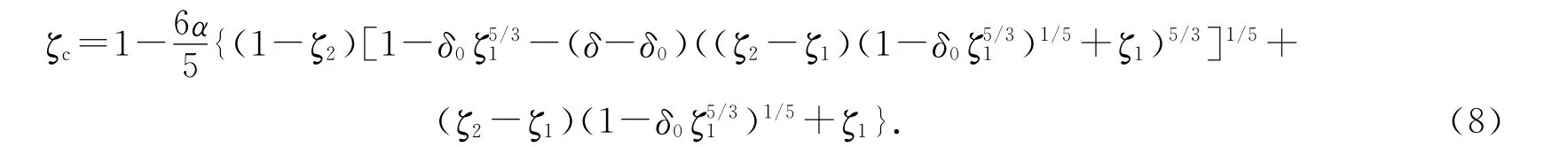
由于天花板处的热羽流（浮升力为g′p，H，new）沿天花板水平扩散过程中与周围热空气（浮升力为g′）相混合，因此将扩散形成的热空气薄层的浮升力g′c近似为g′p，H，new与g′的算术平均值．同时，由于热羽流沿天花板水平扩散过程中紧靠天花板处的空气与周围空气混合的可能性较小，因此将天花板处通风口排出空气的浮升力g′out近似看作与天花板处热羽流的浮升力g′p，H，new相等；于是，天花板处热空气薄层和排出空气的无量纲浮升力分别为

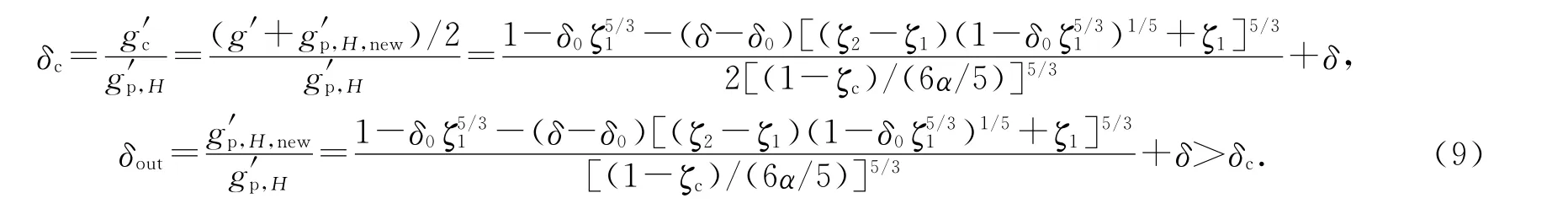
通风过程中室内区域的物理量守恒方程可以表示为

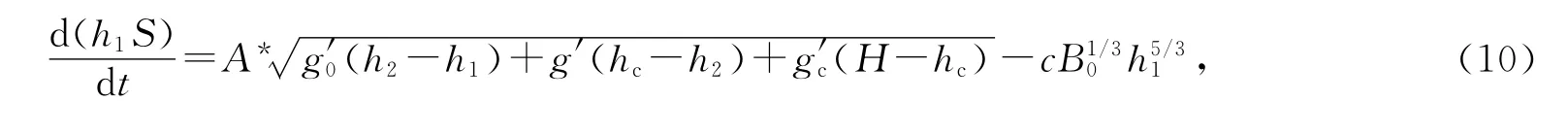
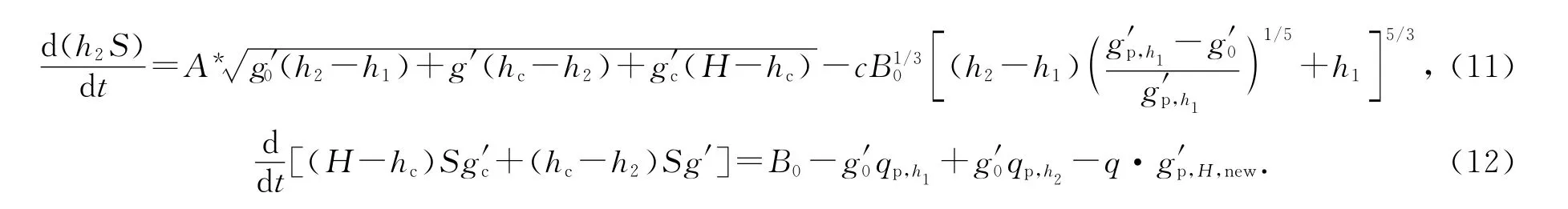
上述方程的无量纲形式分别为

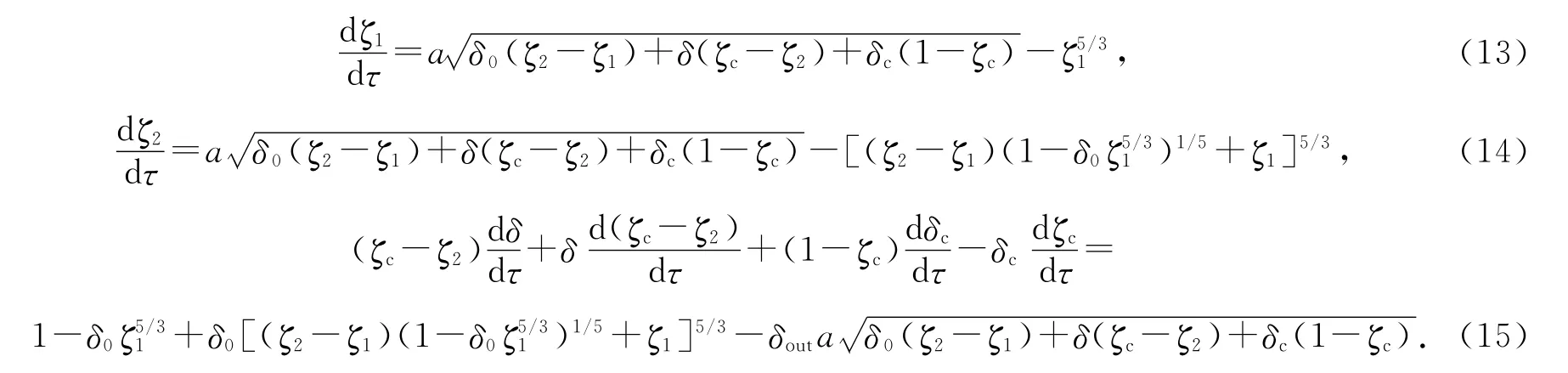
方程（8），（9），（13）～（15）即为该通风模式下瞬态通风过程的改进模型，由于该模型假设通风过程中室内由4个区域组成，因此也称为四温度层模型．模型方程要求ζc≥ζ2，于是将满足ζc≥ζ2 的最初时刻τ0取为初始时刻，该时刻之前的通风过程利用F－W 模型求解，将求解得到的τ0时刻参数ζ1，i，ζ2，i和δi作为改进模型中相应参数的初始值；因此，改进模型的初始条件为ζ1＝ζ1，i，ζ2＝ζ2，i，δ＝δi．

改进模型与F－W 模型的主要区别在于它认为室内新形成的热空气层并不是充分混合的，而是由紧靠天花板的热空气薄层及其下方的热空气层两部分组成，并将天花板处热空气薄层的浮升力近似为天花板处热羽流的浮升力与周围热空气层浮升力的平均值，将排出空气的浮升力近似为热羽流浮升至天花板时的浮升力．

本研究利用Mathematica 7．0软件求解F－W 模型和改进模型的微分方程组，数值方法为显式RungeKutta法．图3给出了a＝0．4，δ0＝0．82条件下，改进模型和F－W 模型预测得到的热分层界面高度与文献［8］2785中实验数据间的相对偏差dr．由图3可知，模型预测结果与实验结果间的相对偏差较小，尤其是关于h2的模型预测结果与实验数据之间的偏差仅在4%以下．图3还表明，多数时刻对应的改进模型预测结果与实验结果间的偏差小于F－W 模型预测结果与实验结果间的偏差，这说明改进模型的预测精度优于F－W 模型．

3 瞬态热压通风过程分析

3．1 瞬态热分层界面高度

图4给出了无量纲的室内初始浮升力δ0为0．2，无量纲有效通风面积a分别为0．2，0．5和1．0条件下热分层界面高度ζ1 和ζ2 随无量纲时间τ的变化过程，图中3条水平细线分别对应着3个a值条件下的稳态热分层界面高度ζss．由图4可知，a越小，ζss越小，这与室内外初始温度相同条件下的热压自然通风类似［4］147，因为稳态热分层界面高度仅取决于a 值，与室内外初始温度条件无关［4］147，［6］22．图4还表明，a越小，通风过程中室内原有热空气层的上界面下移低于稳态热分层界面的现象越明显，这也与室内外初始温度相同条件下的热压自然通风类似［4］147．

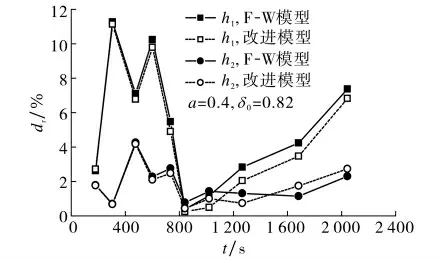
图3 分层界面高度的模型预测结果与实验结果间的偏差Fig．3 The relative deviation，dr，between theoretical and experimental values of interface height

图5 给出了a为0．2，δ0分别为0．2，0．8，1．5条件下热分层界面高度ζ1 和ζ2 随无量纲时间τ的变化过程，图中的水平细线表示热分层界面的稳态高度ζss．该图说明，室内的初始浮升力δ0越小，瞬态热分层界面高度ζ1 和ζ2 均越小，这就意味着室内原有热空气层上界面的高度变化越快而下界面的高度变化越慢．图5还说明，δ0越小，通风过程中室内原有热空气层的上界面下移低于稳态热分层界面的现象越明显．对δ0较大的情形，上界面下移过程中仍然会低于ζss线，尽管该现象并不明显．例如，在δ0＝1．5的条件下，ζ2，min＝0．463 4 ＜ζss＝0．463 751．

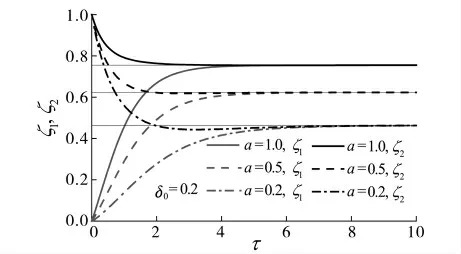
图4 不同a条件下的瞬态热分层界面高度Fig．4 The dimensionless interface height，ζ1andζ2，as a function ofτfor different values ofa

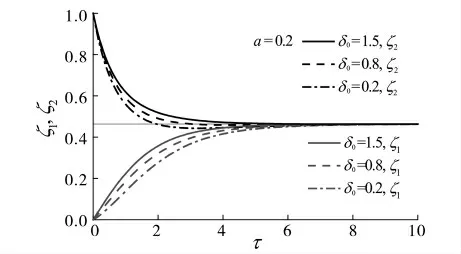
图5 不同δ0 条件下的瞬态热分层界面高度Fig．5 The dimensionless interface height，ζ1andζ2，as a function ofτfor different values ofδ0

3．2 瞬态通风量

通风过程的瞬态通风量q对应的无量纲形式为Q＝a［δ0（ζ2－ζ1）＋δ（ζc－ζ2）＋δc（1－ζc）］1／2．图6表示δ0为0．2，无量纲有效通风面积a分别为0．2，0．5，1．0条件下无量纲的瞬时通风量Q．该图表明，有效通风面积越小，无量纲的瞬时通风量越小，稳态时的无量纲通风量也越小．图7表示a为0．2，δ0分别为0．2，0．8，1．5条件下无量纲的瞬时通风量Q．由图7可知，室内初始浮升力越小，无量纲的瞬时通风量越小，但稳态时的无量纲通风量Qss相同，这是因为Qss仅取决于a值．

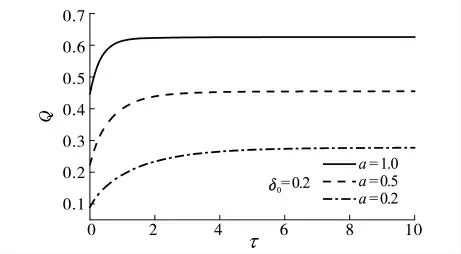
图6 不同a条件下的无量纲瞬时通风量QFig．6 Dimensionless flow rate Qas a function of τfor different values ofa

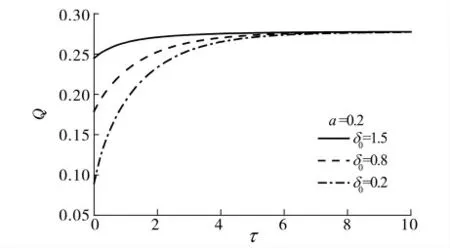
图7 不同δ0 条件下的无量纲瞬时通风量QFig．7 Dimensionless flow rate Qas a function of τfor different values ofδ0

4 结论

1）改进模型对室内初始温度较高条件下瞬态热压通风过程的预测精度优于F－W 模型．

2）无量纲的有效通风面积越小，通风过程中室内原有热空气层的上界面下移低于稳态热分层界面的现象越明显，无量纲的瞬时通风量越小，稳态时的热分层界面高度和无量纲通风量也越小．

3）室内空气的初始浮升力越小，通风过程中室内原有热空气层的上界面下移低于稳态热分层界面的现象越明显，瞬态热分层界面高度ζ1 和ζ2 均越小，无量纲的瞬时通风量也越小，但稳态时的热分层界面高度和无量纲通风量均不变．

［1］ LINDEN P F，LANE－SERFF G F，SMEED D A．Emptying filing boxes：the fluid mechanics of natural ventilation［J］．J Fluid Mech，1990，212：309－335．

［2］ LI Yuguo．Buoyancy－driven natural ventilation in a thermally stratified one－zone building［J］．Build Environ，2000，35（3）：207－214．

［3］ KAYE N B，HUNT G R．Heat source modeling and natural ventilation efficiency［J］．Build Environ，2007，42（4）：1624－1631．

［4］ KAYE N B，HUNT G R．Time－dependent flows in an emptying filling box［J］．J Fluid Mech，2004，520：135－156．

［5］ FITZGERALD S D，WOODS A W．Transient natural ventilation of a room with a distributed heat source［J］．J Fluid Mech，2007，591：21－42．

［6］ BOWER D J，CAULFIELD C P，FITZGERALD S D，et al．Transient ventilation dynamics following a change in strength of a point source of heat［J］．J Fluid Mech，2008，614：15－37．

［7］ SANDBACH S D，LANE－SERFF G F．Transient buoyancy－driven ventilation：part 1．modelling advection［J］．Build Environ，2011，46（8）：1578－1588．

［8］ FITZGERALD S D，WOODS A W．Transient natural ventilation of a space with localised heating［J］．Build Environ，2010，45（12）：2778－2789．

［9］ TURNER J S．Turbulent entrainment：the development of the entrainment assumption，and its application to geophysical flows［J］．J Fluid Mech，1986，173：431－471．

［10］ HUNT G R，COOPER P，LINDEN P F．Thermal stratification produced by plumes and jets in enclosed spaces［J］．Build Environ，2001，36（7）：871－882．