一类物价瑞利模型在小周期扰动下的Hopf分支
吕堂红,周林华
(长春理工大学 理学院,长春130022)
近年来,许多学者基于平均法[1]、多尺度法[2]、摄动法[3]和谐波平衡法[4]等方法研究了时滞微分系统的动力学行为,对滞后型泛函微分方程的周期扰动Hopf分支更是倍加关注[5-9].上述方法[1-4]主要是针对一个正在产生Hopf分支的时滞微分系统,而加上外界微小的周期扰动后新的扰动系统的周期轨道将产生哪些新的运动规律,这正是本文需要探讨的数学问题.

目前,关于具时滞物价瑞利方程的研究已有很多结果[9-11].笔者[10]曾利用指数多项式的τ-D 划分法讨论模型(0)平衡点的稳定性和Hopf分支的存在性,给出了在(τ,γ)参数平面上的Hopf分支图;曹忠威[9]只讨论了l=1时模型(0)的周期扰动Hopf分支问题,而对l≠1的情形未给予研究.为此,笔者将对文献[9]中的问题作进一步的推广,讨论l≠1时模型(0)的周期扰动Hopf分支的动力学性质.
1 物价瑞利模型Hopf分支的存在性



当β1=0时,系统(3)线性部分的特征方程为

引理1[10]445若k0=(sinσ0r)/σ0,σ0=σ0(r)是方程σ2=cosσr在(0,π/(2r))上的唯一解,则
1)方程(4)有一对共轭复根λ1,2=α(μ)±iσ(μ),这里α,σ是实数,且α(0)=0,σ(0)=σ0>0;
2)当μ=0时,方程(4)的特征根除λ(0),¯λ(0)外,其余特征根皆有严格的负实部;
3)当β1=0时,方程(3)在μ=0时存在Hopf分支,若分支产生在μ>0(μ<0)方向,则方程(3)的分支周期解为上临界稳定(下临界不稳定)的.
2 物价瑞利模型周期扰动Hopf分支的存在性与稳定性
下面利用类似于文献[8]115-117的分析方法,讨论系统(3)在β1≠0时的分支情形.不妨设σ0为系统(3)的临界固有Hopf分支频率,于是必须考虑的问题是:当外界的周期扰动频率分别为σ0,nσ0,σ0/n,mσ0/n(m,n∈Z+,m,n≠1且互质)时,系统(3)产生的周期扰动Hopf分支的动力学性质.
2.1 系统的简化和积分平均
首先对系统(3)进行尺度变换,令x→εx,y→εy,μ→εμ,β1→εβ1,然后将变换后的系统写成滞后型泛函微分方程的形式.令C=C([-r,0],R2),对任意φ∈C,定义L(εμ)为C[-r,0]到R2上的线性算子族,于是由Riesz表示定理知,存在一个有界变差矩阵η(θ,μ):θ∈[-r,0],使得L(εμ)φ =,这里取dη(θ,εμ)是Diracδ-函数;因此,可将方程(2)写成向量的形式:
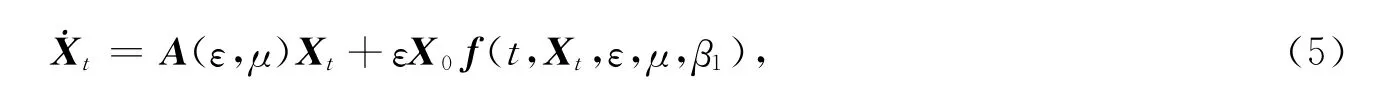
其中Xt=(xt,yt)T.对φ ∈C[-r,0],定义由文献[5]26知,当θ=0时,方程(5)就是方程(3).设方程(4)的一对纯虚根为Λ ={iσ0,-iσ0},则存在BC 的一个直和分解:BC =PΛ⊕QΛ,其中PΛ是算子A 相应于Λ 的特征空间,QΛ是其补空间.
现在将方程(5)的解Xt分解到PΛ和QΛ上去.此时方程(5)可以分解为
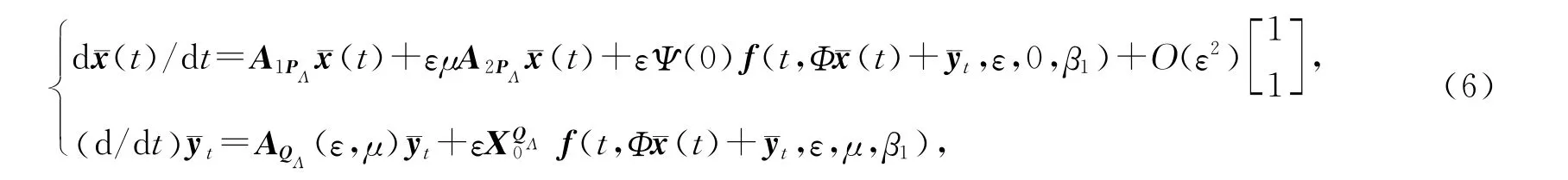
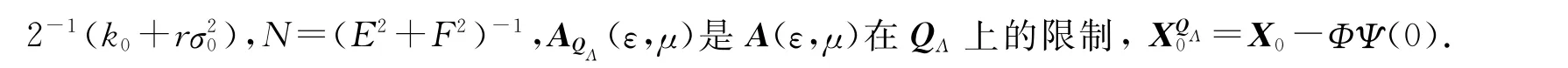
下面对系统(6)的前2个方程进行积分平均[12].对系统(6)作变换:令ωt=τ,则¯x(t)=u(τ),
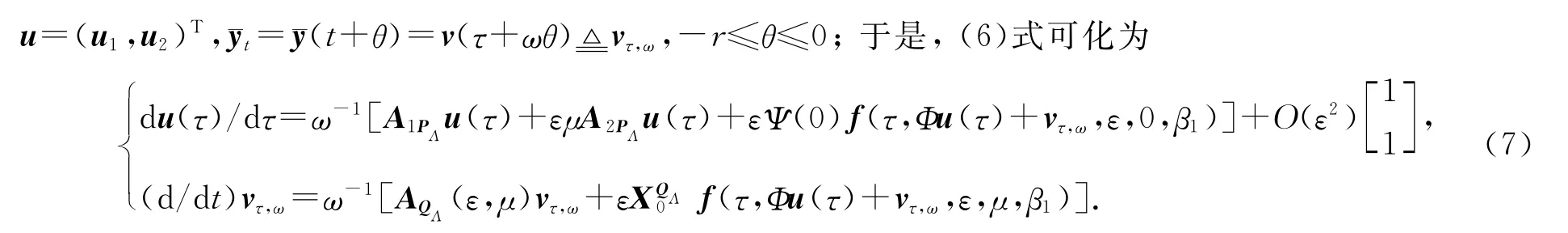
2.2 调和解、次调和解、超调和解和超次调和解的存在性与稳定性
首先,给出系统(3)在共振情形下(J=1)4种不同分支周期解的稳定性分析.
定理1对于系统(3),总存在ε0>0,使得对任意的ε∈(0,ε0),当μ>0(μ<0)时,系统(3)在原点附近的二维流形上存在不稳定(稳定)的调和解分支,其近似表达式为
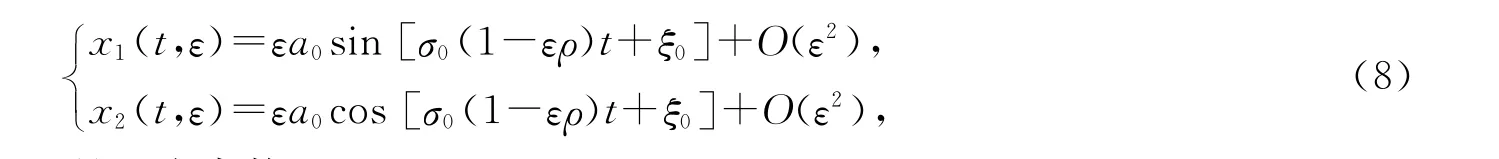
其中μ=O(ε),β1=O(ε),ξ0 是一个常数,
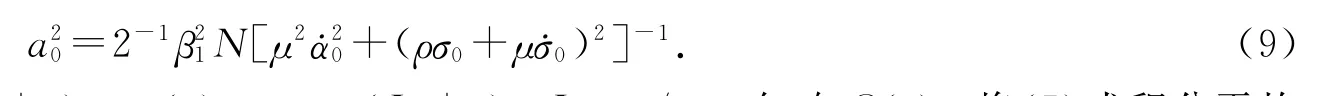
证明 令u1(τ)=~asin(Jτ+ξ),u2(τ)=~acos(Jτ+ξ),J=σ0/ω0,忽略O(ε),将(7)式积分平均后化为

其中ρ为由ω=ω0(1-ερ)定义的一个去谐参数,θ=arctan(E/F).令d~a/dτ=0,dξ/dτ=0,解得方程(10)的非平凡解a0,它对应于系统(2)的一个周期解,并满足方程(9).显然,若(10)式对应的变分方程有解eλετ/ω0,则λ 满足的特征方程为(μ˙α0-λ)2+(ρσ0+μ˙σ0)2=0,特征根为λ1,2=μ˙α0±i(ρσ0+故若μ>0(μ<0),则Reλ1,2>0(Reλ1,2<0).证毕.
然后,依次取J=1/n,J=n,J=m/n(m,n∈Z+,m,n≠1且互质),讨论系统(3)在次调和共振、超调和共振和超次调和共振情形下分支周期解的存在性和稳定性.
定理2对于系统(3),总存在ε0>0,使得对任意的ε∈(0,ε0),当μ>0(μ<0)时,随着激励频率分别接近于σ0,nσ0,σ0/n,mσ0/n,系统(3)在原点附近的二维流形上存在稳定(不稳定)的任意阶次调和解分支、超调和解分支和超次调和解分支,其近似表达式为

其中μ=O(ε2),β1=O(ε2),ρ=O(ε),
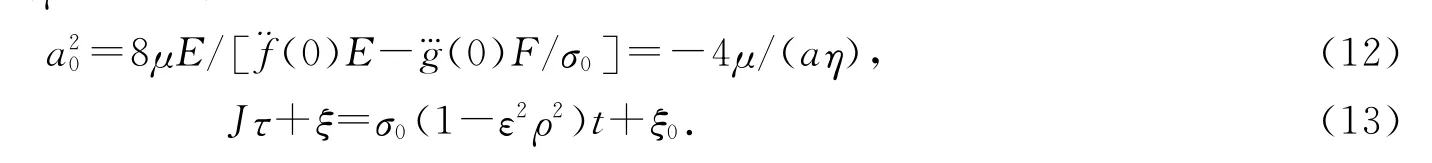
证明 对系统(3)进行尺度变换,令x→εx,y→εy,μ→ε2μ,β1→ε2β1,ρ→ερ,忽略O(ε2)项,再进行积分平均,得令d~a/dτ=0,解得a20如(12)式所示,易算出˙F1(a0)=-ε2μENσ0/ω0;于是,当μ>0时,˙F1(a0)<0;当μ<0时,˙F1(a0)>0;因此,当μ>0(μ<0)时,对应的次调和解、超调和解和超次调和解均为稳定的(不稳定的).再由,可得方程(13).证毕.
2.3 拟周期解的存在性与稳定性
最后,给出系统(14)在二阶次调和共振情形下(J=1/2)拟周期解的稳定性分析.将方程

改写为如下形式:

对系统(15)进行尺度变换,令x→ε1/2x,y→ε1/2y,μ→εμ,则(15)式可化为

使用前述的方法计算,并忽略O(ε)项,然后进行积分平均,可得
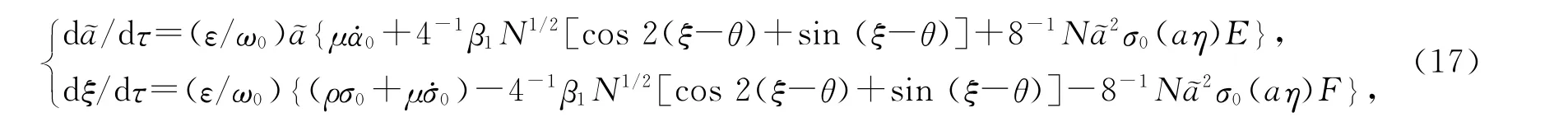
其中θ=arctan(E/F).令d~a/dτ=0,dξ/dτ=0,解得非平凡解a0满足的方程为
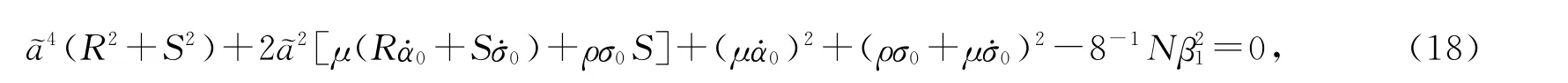
其中R=8-1Nσ0(aη)E,S=-8-1Nσ0(aη)F.由方程(18)可以分析出其正根的分布情况.
引理2设a01,a02由下式定义:
1)当μ(R˙α0+S˙σ0)+ρσ0S<0,[(μ˙α0)2+(ρσ0+μ˙σ0)2]>[μ(R˙σ0-S˙α0)+ρσ0R]/(R2+S2)时,方程(18)有两个正实根a01,a02,并且a01<a02;
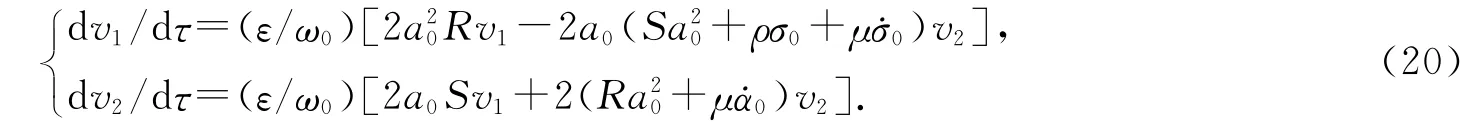
设方程(20)的变分方程有形如eλετ/ω0的解,则λ满足的特征方程为
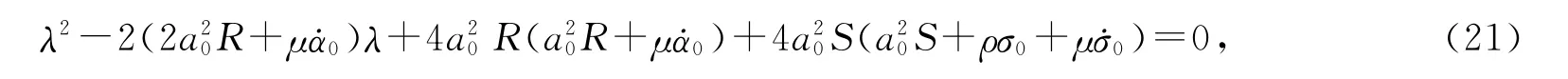
引理31)若非平凡解a0满足下述条件,则它始终是稳定的:

2)若解a01不满足条件(22),则其始终不稳定;
3)若解a02满足条件(22),则其是稳定的;若解a02不满足条件(22),则a0对应的分支周期解将失去稳定性,且对应的变分方程(20)在μc=-2a20R/˙α0处产生Hopf分支;
4)当μ=μc 时,特征方程(21)有一对纯虚根±iωc,且Reλ′(μc)=˙α0>0,其中

下面考虑平均方程(17)在(a0,ξ0)处的变分方程.令~a=a0+v1,ξ=ξ0+v2,可得到
引入新的时间变量¯t=ετ/ω0,作线性变换.令¯μ=μ-μc,当¯μ=0时,(23)式可化为
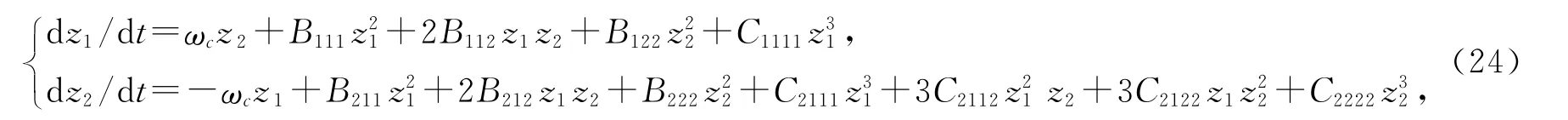
其中B111=2α+2a20S+a20R2/S,B112=ωcR/(2S),B122=ω2c/(4a20S),B211=(2a0/ωc)(2a30R3/S-6a30RS-4a0αR),B212=2a20R2/S -a20S -α,B222=2ωcR/S,C1111=(4/3)a20R,C2111=(2a0/ωc)[a30R4/S2+(4/3)a0S(a20S+α)-(10/3)a30R2],C2112=a20R3/S2-(2/3)a20R,C2122=ωcR2/(2S2),C2222=ω2cR/(4a20S2),α=ρ+μc˙σ0,a20=-μ˙α0/(2R).
由规范形方法[13]可求得C1(0)=¯R+i¯S,这里¯R,¯S 由Bijk和Cijkl表出,因此有如下结论.
定理3对于系统(14),总存在原点附近的一个二维积分流形,使得其上的分支周期解可由下列公式描述:

1)分支方向由μ2确定:μ2>0(μ2<0),方程(14)的分支周期解为上临界的(下临界的);
2)分支周期解的稳定性由β2确定:β2>0(β2<0),方程(14)的分支周期解是不稳定的(稳定的);
3)分支周期解的周期大小由τ2确定:τ2>0(τ2<0),方程(14)的分支周期解将逐渐增大(逐渐减小).
定理4方程(17)在(a0,ξ0)附近存在分支周期解和拟周期解的近似表达式分别为
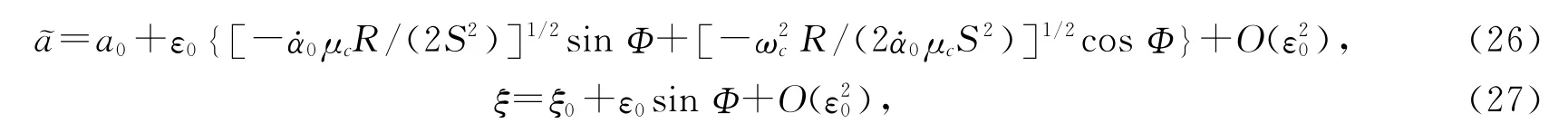
其中 是任意常数.
[1] LAKRIB M.The method of averaging and functional differential equations with delay[J].Inter J Math & Math Sci,2001,26(8):497-511.
[2] KLOSEK M M.Multiscale analysis of effects of additive and multiplicative noise on delay differential equations near a bifurcation point[J].Acta Phys Pol B,2004,35(4):1387-1406.
[3] AMINIKHAH H,HEMMATNEZHAD M.An effective modification of the homotopy perturbation method for stiff systems of ordinary differential equations[J].Appl Math Lett,2011,24(9):1502-1508.
[4] LIU Liping,THOMAS J P,DOWELL E H,et al.A comparison of classical and high dimensional harmonic balance approaches for a Duffing oscillator[J].J Comput Phys,2006,215(1):298-320.
[5] NAMACHCHIVAYA N Sri,ARIARATNAM S T.Periodically perturbed Hopf bifurcation[J].SIAM J Appl Math,1987,47(1):15-39.
[6] 丁丹军.具时滞离散和分布BAM 神经网络的全局渐近稳定性[J].扬州大学学报:自然科学版,2009,12(4):1-5.
[7] 刘宣亮,孟笑莹.三维系统中一族闭轨在周期扰动下的分支[J].系统科学与数学,2009,29(8):1034-1043.
[8] 殷红燕.向日葵方程的周期扰动Hopf分支[J].中南民族大学学报:自然科学版,2010,29(4):115-117.
[9] 曹忠威.具时滞的物价瑞利方程的周期扰动Hopf分支[D].长春:东北师范大学,2006.
[10] 吕堂红,刘振文.具时滞物价瑞利方程的Hopf分支[J].吉林大学学报:理学版,2009,47(3):441-448.
[11] 吕堂红,周林华.双时滞物价瑞利方程的Hopf型和余维2型分支分析[J].吉林大学学报:理学版,2012,50(3):409-416.
[12] HALE J K.Ordinary differential equations[M].Berlin:Springer-Verlag,1977:119-124.
[13] HASSARD B D,KAZARINOFF N D,WAN Y H.Theory and applications of Hopf bifurcation[M].Cambridge:Cambridge University Press,1981:139-144.

