河道可溶性污染物横向扩散的理论研究
陆伟刚,周秀彩
(1.扬州大学 水利科学与工程学院,江苏 扬州225127;2.江苏省水利勘测设计研究院有限公司,江苏 扬州225009)
目前,城市化的发展直接或间接地改变着水环境,可用水资源日益减少,以致影响了人民的生活质量和社会总体福利水平[1],减污、治污工作迫在眉睫.为此,必须研究污染物在水中扩散输移的过程,其主要方法有理论分析、物理实验和数值模拟等[2-6].有关污染物的降解过程,国外对水质模型研究较多[7-11];国内也开展了一些研究,如吴迪军等[12]建立了水污染扩散的二维数学模型,采用有限差分法求解水动力方程和污染扩散方程,获得污染物浓度的时空分布;武周虎等[13]给出了河流污染物浓度的二维解析计算方法及污染物的无量纲浓度分布方程;李娜[14]结合WebGIS技术,提出了水污染事故应急分析中的一维水体污染扩散模拟实现方案.本文主要探讨污染物横向扩散过程,对现有水力学理论公式进行简化,建立二维流场污染物扩散的数学模型,以揭示污染物扩散过程中期浓度在平面流场中随时间的变化规律,为预报纳污水域中水体受污染的程度、水质的保护、水资源的开发和利用提供依据.
1 横向扩散浓度
污染物通过在水体中溶解扩散以及随流输移而扩大影响范围,其与水体的混合过程通常可分为3个阶段:第1阶段是发生在排污口附近水域,通常称为近区,其他2个阶段发生过程距离排污口较远,称为远区;第2阶段可作为二维扩散问题处理;第3阶段可作为一维纵向离散问题处理.
在通常情况下,近区问题关联因素众多,须作为三维模型进行研究,但在某些特定条件下可以化为二维模型处理.一般河道,其水深比河宽小得多,所以污染物在垂向的混合几乎在瞬间完成,随后主要是横向扩散过程.若污染物为中性物质,接近纳污水体重度,则三维扩散可简化为二维扩散,本文着重讨论污染物在特定条件下的二维扩散问题.
假设明渠属于理想的顺直河流,则扩散系数可视为常数;河流以纵向平流作用为主,可忽略二维扩散方程[15]右边第1项;垂向以混合扩散作用为主,可忽略垂向平流作用,故二维扩散方程左边第3项也可忽略;因分子扩散作用很小,故其方程第3,4项可忽略,则污染物的二维扩散方程可变为

式中c为污染物浓度,t为污染物扩散时间,U 为水流纵向平均流速,Ey为河流横向扩散系数,K 为污染物的衰减速度常数,x,y 分别为河流的纵向和横向坐标.
通常情况下污水连续排放,为时间连续源,本文着重分析连续点源排放问题.设投放物质强度为m,则连续点源二维扩散的解为
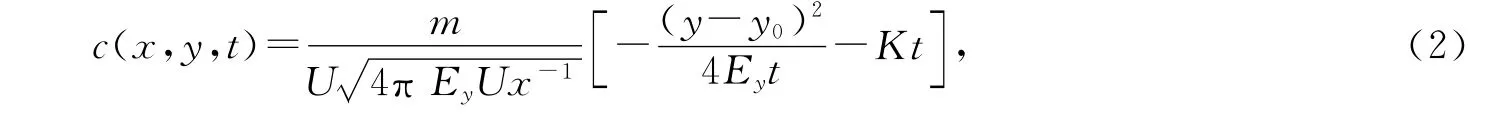
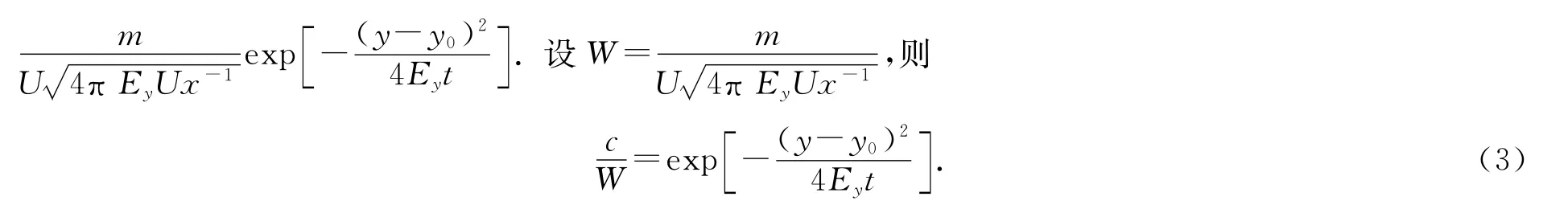
式中y0为污染点源与坐标原点的横向距离.对于不可降解物质,K=0,式(2)变为c(x,y,t)=设河道宽度为B,y0分别为0,0.3B,0.5B,0.7B时的污染物扩散浓度分布示于图1.由图1可以看出:浓度峰值位于排放点处.若污水排放口在河道中心线上,则浓度的分布对称于河道中心线.从实绘图形分析来看,结论是合理的.污染物排放点定为坐标原点,y0=0,则c(x,y,t)=为计算方便,取1 次反射,并忽略污染物降解项,得
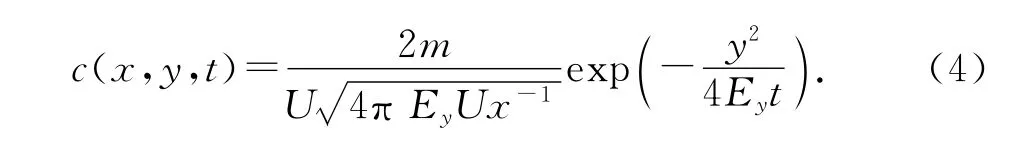
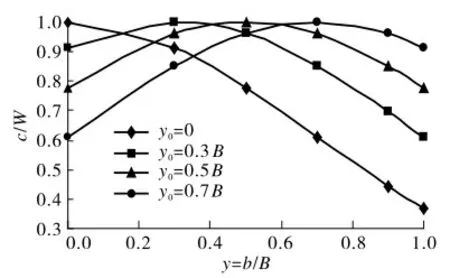
图1 y0 分别为0,0.3B,0.5B,0.7B 时的横向浓度分布Fig.1 Abeam concentration distribution of pollutants with y0=0,0.3B,0.5B,0.7B
2 横向混合时间
设垂向扩散完成的时间尺度为tz,横向扩散完成的时间尺度为ty,因tz与H2/(4Ez),ty与B2/(4Ey)成正比,所以

式中H 为水深,B 为河宽,Ey为横向扩散系数,Ez为垂向扩散系数.通常取Ey=0.6 Hu*,Ez=0.067 Hu*,其中u*为垂线上的渠底摩阻流速,则

河流具有代表性的深宽比为H/B=1/30,于是

由此可见,污染物横向扩散时间的长短与其垂向扩散的时间有关.
3 垂向混合时间
在通常情况下,污染物为连续源排放,本文讨论与水体密度相当的污染物溶质,接纳水体是明渠均匀流,河流含沙量较小.
工程中假定为顺直明渠,扩散系数粗略认为是常数;对于河道纵向,平流作用远大于离散作用,所以污染物二维扩散方程可以忽略右边离散项;对于河道垂向,混合扩散作用远大于平流作用,因此可以忽略污染物扩散方程的左边平流项;同横向扩散一样,也可忽略右边第3,4项,则污染物二维扩散方程可变为

式中z为河流的垂向坐标.
设m 为连续源单位时间投放的物质强度,则时间连续点源扩散方程可解为
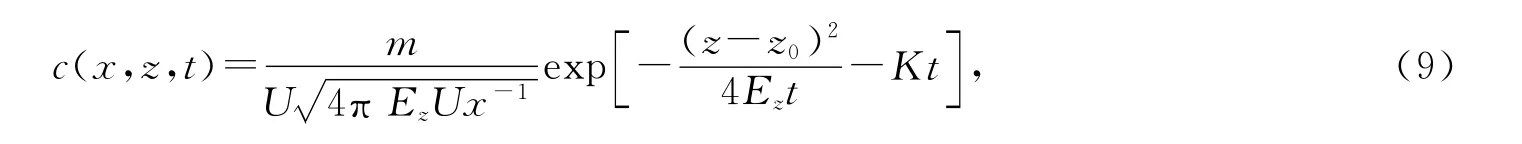
式中z0为污染点源与坐标原点的垂向距离.此时可粗略计算排污口下游控制断面的污染物浓度,坐标原点设在污染源排放中心点处,z0=0,仅反射1次,则
通常污染源多为表面排放,此时坐标原点若设在污染源排放中心点处,则z0=0.假设在水面(z=0)及河底(z=H)处完全反射,则那么式(9)可写为
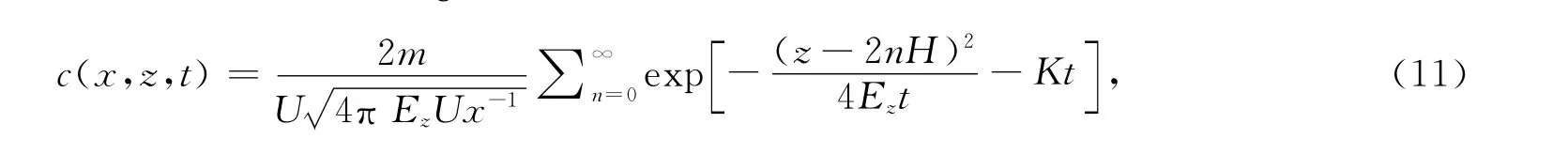
式中n为水面及河底反射次数.
对于连续排放的等强度污染源,其最大与最小浓度分别出现在水面与河底处.设c(x,0,t)为河道表面浓度,c(x,H,t)为河底浓度,则河底与水面的浓度比值为

定义污染物在近区垂向均匀混合距离lmin为污染排放点到垂向均匀混合点的纵向长度.取n=1,由c(x,H,t)=R c(x,0,t),列出方程
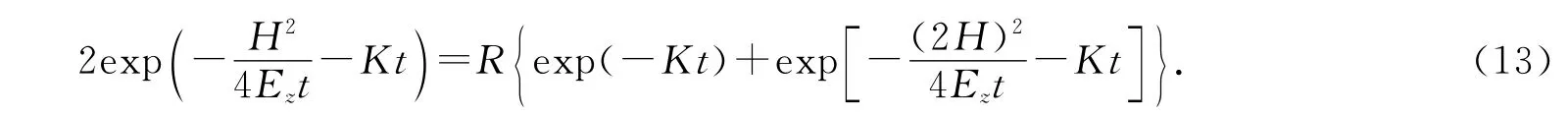

4 实验验证
若某一方向上污染物浓度差在5%以内,则可认为该方向上污染物已完全均匀混合,此时取R=95%,则污染排放点到垂向均匀混合点的纵向长度为
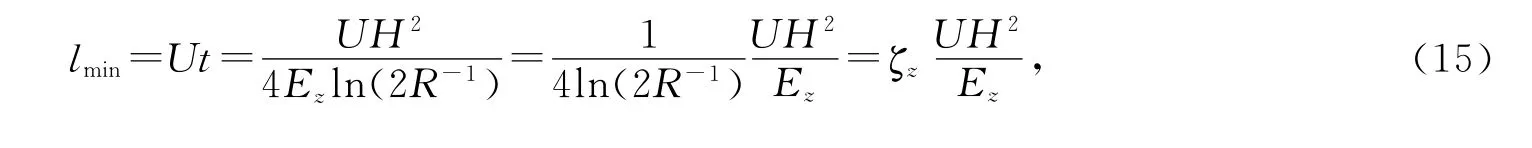
本文用文献[16]的实验结果加以验证,比较情况列于表1.由表1可见,垂向均匀混合纵向距离的计算值与实测值结果较为接近.

表1 垂向均匀混合纵向距离的计算值与实测值比较Tab.1 Comparison between calculated and measured values for the fore-and-aft distance of vertical uniformity mixing
[1] 朱春龙,周明耀,王文远.城市水环境控制决策支持系统的研究[J].扬州大学学报:自然科学版,2001,4(1):58-62.
[2] BASHA H A.Analytical model of two-dimensional dispersion in laterally nonuniform axial velocity distributions[J].J Hydraul Engin,1997,123(10):853-862.
[3] CHAU K W.Transverse mixing coefficient measurements in an open rectangular channel[J].Adv Environ Res,2000,4(4):287-294.
[4] BOXALL J B,GUYMER I,MARION A.Locating outfalls on meandering channels to optimise transverse mixing[J].J Water Environmen,2002,16(3):194-198.
[5] CHEN Y,LIU Z,SHEN M.The numerical simulation of pollutant mixing zone from riverside discharge outlet in Three Gorges Reservoir[C]//Proceedings of the 6th International Conference on Hydrodynamics.Perth Western Australia:[s.n.],2004:401-408.
[6] JEONG S,YEON K,HUR Y,et al.Salinity intrusion characteristics analysis using EFDC model in the downstream of Geum River[J].J Environ Sci,2010,22(6):934-939.
[7] MISHRA A,KAR S,RAGHUWANSHI N S.Modeling nonpoint source pollutant losses from a small watershed using HSPF model[J].J Environ Eng,2009,135(2):92-100.
[8] SALTERAIN A,SANCHO L,RODRÍGUEZ E,et al.Development and verification of a new simulation tool for water quality prediction in the Ebro River[J].Water PollutⅦ:Modell,Meas &Predict,2003(9):13-22.
[10] FACCHI A,GANDOLFI C,WHELAN M J.A comparison of river water quality sampling methodologies under highly variable load conditions[J].Chemosphere,2007,66(4):746-756.
[11] GRONEWOLD A D,QIAN S S,WOLPERT R L,et al.Calibrating and validating bacterial water quality models:A Bayesian approach[J].Water Res,2009,43(10):2688-2698.
[12] 吴迪军,陈建国,黄全义,等.水污染扩散的二维数值模拟及其可视化[J].武汉大学学报:工学版,2009,42(3):296-300.
[13] 武周虎,武文,路成刚.河流混合污染物浓度二维移流扩散方程的解析计算及其简化计算的条件Ⅱ:顺直河流考虑边界反射[J].水利学报,2009,40(9):1070-1076.
[14] 李娜.基于WebGIS的一维水体污染扩散模拟的实现[J].现代电子技术,2011,34(11):60-62.
[15] 杨志峰,王烜,孙涛,等.环境水力学原理[M].北京:北京师范大学出版社,2006:53-59.
[16] 杜彦良,褚君达.河流连续点源的垂向混合规律研究及其应用[J].环境科学学报,2000,20(6):699-703.

