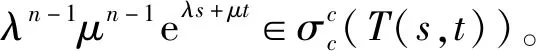指数有界双参数n阶α次积分C半群的谱映射定理
周裕然,赵华新,周 阳
(延安大学 数学与计算机科学学院,陕西 延安 716000)
谱的相关理论是算子半群主要研究的内容之一,许多学者研究了谱的相关性质[1-3]。文献[4]研究了双参数C半群的一些结果及其相关性质;文献[5]给出了n阶α次积分C半群的概念、预解集以及次生成元等问题;文献[6]讨论了双参数n阶α次积分C半群及其性质;文献[7]研究了指数有界双连续n阶α次积分C半群的生成定理;文献[8-11]研究了相关半群的谱映射定理。本文在上述研究的基础上,利用指数有界双参数n阶α次积分C半群的点谱、剩余谱、连续谱的定义,讨论了指数有界双参数n阶α次积分C半群的谱映射定理。
1 预备知识
在本文中,X为无限维的复Banach空间,B(X)是X上有界线性算子全体所成的Banach代数;D(A)为线性算子A的定义域,设n∈N,α≥0。
T=0当且仅当存在n≥0使
JnT(t,s)=0,t,s≥0。
定义1[6]设n∈N,α≥0,C∈B(X)是单射,算子族{T(t,s):∀t,s≥0}⊂B(X)。
被称为指数有界双参数n阶α次积分C半群,则以下条件成立:

∀t,s≥0;
(2)存在闭线性算子A=(A1,A2),满足
∀x∈X,t,s≥0,JnT(t,s)∈D(A),
∀x∈D(A),t,s≥0,
(3)存在M≥0,ω∈R使
‖T(t,s)‖≤‖C-1‖Meω(t+s),∀t,s≥0。
称A=(A1,A2)是{T(t,s):∀t,s≥0}⊂B(X)的次生成元,把G(M,ω,C,t,s)记为X内的所有指数有界双参数n阶α次积分C半群。
定义2[6]设A为指数有界双参数n阶α次积分C群的次生成元,则称集合:{aλ+bμ|λn-1μn-1((aλ+bμ)n-T(t,s))-1C∈B(X),a,b∈R,t,s≥0}为指数有界双参数n阶α次积分C半群{T(t,s):∀t,s≥0}的预解集,称集合C/ρc(T(t,s))指数有界双参数n阶α次积分C半群{T(t,s):∀t,s≥0}的谱,记为σc(T(t,s))。
定义3[6]设{T(t,s):∀t,s≥0}是复Banach空间X上的指数有界参数n阶α次积分C半群,分别称集合
σpc(A)={aλ+bμ:((aλ+bμ)n-A)-1C不存在},

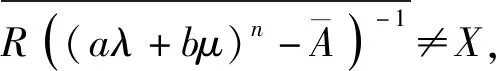
2 主要结果
定理1 设{T(s,t)}s,t≥0是由A次生成的指数有界双参数n阶α次积分C半群。令
x∈X,s,t≥0,λ,u∈R。则
(1)∀x∈X,
(λn-1μn-1((aλ+bμ)n-A))Bλ,μ(s,t)x=
-λn-1μn-1C·eλs+μtx-λn-1μn-1T(s,t)x;
(2)∀x∈D(A),
Bλ,μ(s,t)(λn-1μn-1((aλ+bμ)n-A))x=
-λn-1μn-1C·eλs+μtx-λn-1μn-1T(s,t)x。
证明由Bλ,μ(s,t)的定义可知,
Bλ,μ(s,t)∈B(X)对x∈X有
λn-1μn-1·
λn-1μn-1·
U1=U2=U3。
λn-1μn-1(λa+μb)nCBλ,μ(s,t)x。
T(s,t)Cx。
λn-1μn-1C2eλs+μtx。
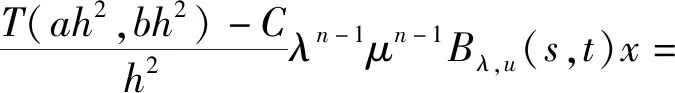
λn-1μn-1(λa+μb)nCBλ,u(s,t)x+
λn-1μn-1T(s,t)x+λn-1μn-1C2eλs+μtx。
λn-1μn-1(λa+μb)nBλ,u(s,t)x+λn-1μn-1T(s,t)x+
λn-1μn-1Ceλs+μtx。
λn-1μn-1(λa+μb)nBλ,μ(s,t)x+λn-1μn-1T(s,t)x+
λn-1μn-1Ceλs+μtx。
所以λn-1μn-1((λa+μb)n-A)Bλ,μ(s,t)x=
-λn-1μn-1Ceλs+μtx-λn-1μn-1T(s,t)x。
∀x∈D(A)有,Bλ,μ(s0,t0)x∈D(A)且
Bλ,μ(s0,t0)λn-1μn-1Ax=
Bλ,μ(s0,t0)λn-1μn-1(λa+μb)nx+
λn-1μn-1Ceλs0+μt0x+λn-1μn-1T(s0,t0)x。
所以有Bλ,μ(s,t)λn-1μn-1((λa+μb)n-A)x=
-λn-1μn-1Ceλs+μtx-λn-1μn-1T(s,t)x。
定理2 设{T(s,t)}s,t≥0是由A次生成的指数有界双参数n阶α次积分C半群,则
esσ(A1)+tσ(A2)⊆σc(T(s,t))。
证明因为A是指数有界双参数n阶α次积分C半群的次生成元,而A1,A2分别为指数有界双参数n阶α次积分C半群T(s,0)和T(0,t)的无穷小次生成元,所以只需要证明
esρ(A1)+tρ(A2)⊇ρc(T(s,t))或者
设λn-1μn-1e(λa+μb)n∈ρc(T(s,t)),则
(-Cλn-1μn-1eλs+μt-λn-1μn-1T(s,t))-1∈B(x)。
令M=(-Cλn-1μn-1eλs+μt-λn-1μn-1T(s,t))-1,
则由定理1,∀x∈X有
λn-1μn-1((λa+μb)n-A)Bλ,μ(s,t)Mx=
(-Ceλs+μtλn-1μn-1-λn-1μn-1T(s,t))Mx=x。
对于∀x∈D(A),有
MBλ,μ(s,t)λn-1μn-1((λa+μb)n-A)x=
M(-Ceλs+μtλn-1μn-1-λn-1μn-1T(s,t))x=x。
由Bλ,μ(s,t)的定义知,M与Bλ,μ(s,t)可交换,则∀x∈D(A)有
Bλ,μ(s,t)Mλn-1μn-1((λa+μb)n-A)x=x。
综上可知,(λn-1μn-1((λa+μb)n-A))=
Bλ,μ(s,t)M∈B(x),故
aρ(A1)+bρ(A2),
从而定理得证。
定理3 设{T(s,t)}s,t≥0是由A次生成的指数有界双参数n阶α次积分C半群,则
esσp(A1)+tσp(A2)⊆ρp(T(s,t))。

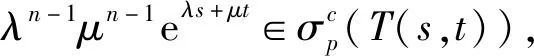
λn-1μn-1(aλk+bμk)n=
证明

从而由定理1知
即∃x0≠0,使得
由定义得λn-1μn-1eλs+μt∈σpc(T(s,t))。
(2)设λn-1μn-1eλs+μt∈σp(T(s,t)),
由定义3知∃x0≠0,使得

-λn-1μn-1Ceλs+μtx-λn-1μn-1T(s,t)x=
λn-1μn-1Ce(λa+μb)lx-λn-1μn-1T(al,bl)x,
λn-1μn-1e-(λa+μb)(l+t)T(a(l+t),b(l+t))x0=
λn-1μn-1e-(λa+μb)le-(λa+μb)tC-1T(al,bl)T(at,bt)x0=
λn-1μn-1e-(λa+μb)lT(al,bl)x0。
所以连续函数l→λn-1μn-1e-(λa+μb)lT(al,bl)x0是以t为周期的周期函数。
由于λn-1μn-1e-(λa+μb)lT(al,bl)x0不恒等于零,所以Fourier函数必有一个不为零,所以∃k∈N,使得
以下证明

令ηk=λn-1μn-1(aλk+bμk)n,
η=λn-1μn-1(aλ+bμ)n,
ξ=λn-1μn-1(aλ0,+bμ0)n,则
λn-1μn-1(ξ-A)-1Cx0=
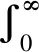
T(a(φ+nt),b(φ+nt))x0dφ=
T(a(φ+nt),b(φ+nt))x0dφ=


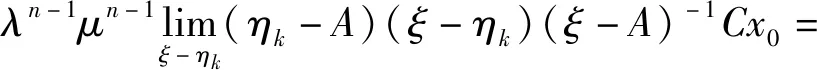
所以λn-1μn-1(ηk-A)xk=0。
而xk≠0,A是闭线性算子,因此
ηk=λn-1μn-1(aλk+bμk)n=
结论得证。
定理4 设{T(s,t)}s,t≥0是由A次生成的指数有界双参数n阶α次积分C半群,若
λn-1μn-1(λa+μb)n∈σ(A),且对于n∈N,
λn-1μn-1(λa+μb)n=
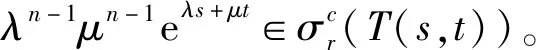
证明若λn-1μn-1(λa+μb)∈σ(A),设(λa+μb)∈σr(A)。由定义3得
则存在x*∈X′,x*≠0,使得
〈x*,λn-1μn-1((λa+μb)n-A)·Cx〉=0。
由λn-1μn-1((λa+μb)n-A)Bλ,μ(s,t)x=
(-C·eλs+μtλn-1μn-1T(s,t))x,
λn-1μn-1((λa+μb)n-A)Bλ,μ(s,t)x=
-C·eλs+μtλn-1μn-1x-λn-1μn-1T(s,t)x,
得〈x*,(-C·eλs+μtλn-1μn-1-λn-1μn-1T(s,t))x〉=0,x∈X。
因此
即R(-C·eλs+μtλn-1μn-1-λn-1μn-1T(s,t))在X中不稠密。
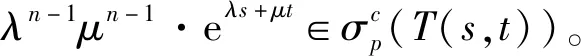
由定理3得∃n∈N,使得
λn-1μn-1(λa+μb)n=
这与定理的已知条件矛盾。
因此(-C·eλs+μtλn-1μn-1-λn-1μn-1T(s,t))-1存在,从而由定义知
定理5 设{T(s,t)}s,t≥0是由A生成的指数有界双参数n阶α次积分C半群,若
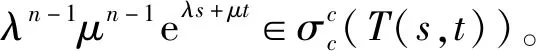

则由定理3得λn-1μn-1(λna+μnb)∈σp(A),与已知条件矛盾。

则由定理4得λn-1μn-1(λna+μnb)∈σr(A),与已知条件矛盾。