双层组合梁的实验研究及理论分析

石昌雨，张 耀，李建光

(兰州交通大学土木工程学院，甘肃兰州730070)

由经典材料力学的纯弯曲理论可知，单一材料矩形截面梁的应力分布沿截面高度呈线性规律分布，横截面在中性轴位置处的正应力为零，距离中性轴最远的上、下边缘处的正应力最大。组合梁大量的应用于工程实践，因为可以充分利用不同材料的性能，从而在强度、刚度、耐腐、耐锈等方面具备优点，且具有良好的经济性。因此，有必要对组合梁受弯时截面的应力分布进行理论与实验研究。

1 实验测试

实验采用钢－铝两种材料组合梁，上下两层梁采用截面尺寸相同的矩形截面，原始数据见表1。双层叠合梁的实验装置见图1。在跨中截面位置沿梁轴向粘贴10个电阻应变片，电阻应变片灵敏系数K=2.22，见图2。

图1 实验装置

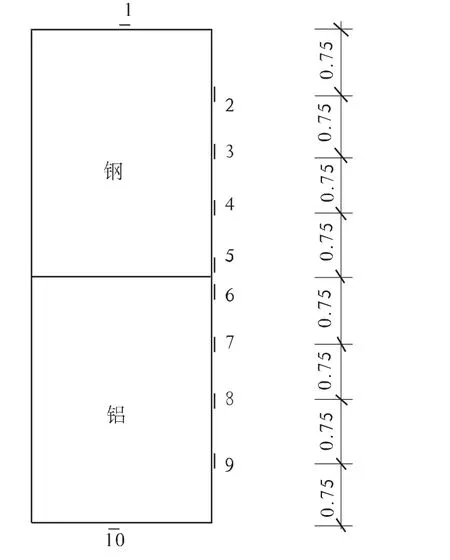
图2 测点布置编号(单位:cm)

全部实验在材料力学多功能试验台上完成，采用DH3818型电阻应变仪采集各测点的应变数据。组合梁上的荷载采用等增量法分级施加，分为4级加载，Pmax=800 kN。荷载增量△P=200 kN。通过弯曲性能试验，得到了双层梁在自由组合和楔块连接两种组合方式下梁截面上的应力分布情况。

实验所得到的自由组合和楔块连接两种组合方式的应变值见表2。

表1 组合梁原始数据

表2 跨中位置各个测点应变值

2 理论分析与计算

2.1 自由组合梁分析

从试验结果可以看出该组合梁上的应变沿梁高分布不连续，整梁的平面假设不再成立。而发现整梁上有两个中性轴，上梁和下梁各自围绕这两个中性轴发生纯弯曲变形，故对单根梁来说可以直接采用平面弯曲梁正应力公式来计算截面上的正应力。事先假定两梁弯曲后接触面处处接触，且梁发生小变形，可得出上梁曲率半径ρ1和下梁曲率半径ρ2相等。根据材料力学可得:

由此可得出两梁中弯矩分配系数:

根据截面法可以求出内力，平衡方程式为:

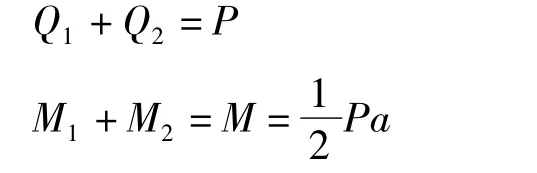
根据以上方程可以求出M1和M2:

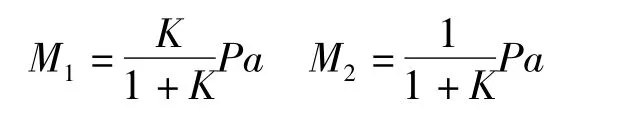
从而可以得出各梁的弯曲正应力:

运用推导出的理论公式计算跨中位置各个测点的应力值，并与实验值进行比较，见表3。

表3 自由组合梁试验结果与计算结果的比较

2.2 楔块连接梁分析

从实验结果可以看出楔块连接梁横截面上的弯曲正应力分布与整体梁类似，梁中只存在一根中性轴，中性轴的位置在钢梁内，加上楔块约束后，梁内产生轴向力，上梁产生压缩—弯曲组合变形，下梁产生拉伸—弯曲组合变形。

由变形条件:上梁下表面与下梁上表面两楔块间的总伸长量相等，即

由式(1)、式(2)和式(3)可以得到

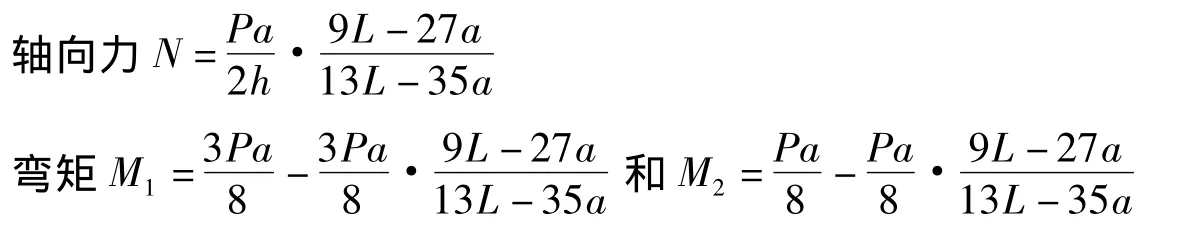
有叠加原理可以得到，横截面上的正应力为:

将推导出的理论公式计算应力值与实验应力值比较，见表4。

表4 楔块连接梁试验结果与计算结果的比较

3 结论

(1)自由组合梁横截面上的正应力沿各自的高度呈线性分布，上下层梁绕各自中性轴转动，两层梁各自产生平面弯曲，仍可采用文献［1］的平面应力公式分别计算各层的应力和强度。

(2)楔块连接组合梁横截面上的弯曲正应力分布于整梁类似，稍有偏差，主要取决于楔块约束的强弱程度。当约束为刚性连接，其应力分布与整梁相同，当约束特弱，其应力分布趋于自由组合。

(3)楔块连接梁要比自由组合梁的承载能力有所提高，与整梁相比，组合梁的强度和刚度都有所下降。

［1］孙训方，方孝淑，关来泰.材料力学［M］.北京:高等教育出版社，2000.

［2］施琪，孙建中.材料力学实验［M］.北京:中国电力出版社，2010.

［3］孙建国.叠梁的分析与实验［J］.力学与实践，2004，26(4):74－76.

［4］王骅，薛伟辰.考虑收缩徐变的钢筋混凝土组合梁变形计算［J］.长安大学学报:自然科学版，2004，24(1):56－60.

［5］鲁书浓，韦林，何大凯.叠合梁实验课程的探讨［J］.实验室研究与探索，2007，26(3):101－109.

［6］何大治.叠合梁极限状态截面应力应变分析［J］.国外建材科技，2004，25(5):54－56.