连续刚构箱梁剪力滞效应分析

李兴坤，郭 凯，周世军

(1.北京铁路局北京工务段，北京100077;2.武汉铁路局武汉桥工段，湖北武汉430000;3.重庆大学土木工程学院，重庆404100)

在剪力滞效应求解理论的基础上，以靖远黄河大桥为工程背景，用当量截面法近似求解该五跨连续刚构桥的剪力滞系数，并与大型有限元分析软件ANSYS的分析结果做比较，分析墩顶有横隔板梁段处的剪力滞效应，找到计算带有横隔板截面剪力滞效应的办法。分析剪力滞效应沿全桥纵向的分布情况，找出负剪力滞效应发生的部位，分析其对桥梁的影响。

1 剪力滞系数

箱形截面剪力滞效应是指在对称荷载作用下，由于翼板的剪切变形造成弯曲正应力沿梁宽方向不均匀的现象。当靠近腹板处的翼板正应力大于翼板中点处正应力时，就称为正剪力滞，反之则称为负剪力滞如图1所示。通常用剪力滞系数来度量剪力滞效应的变化规律，其定义为:

式中:σmax为考虑剪力滞效应所求得的截面最大正应力;σ为按初等梁理论所求得的正应力。

2 工程简介

靖远黄河大桥全长620 m，主桥上部采用52 m+3×90 m+52 m预应力混凝土变截面刚构连续组合体系，下部桥墩采用双薄壁墩钻孔灌注桩基础，见图2。横截面测点布置见图3。

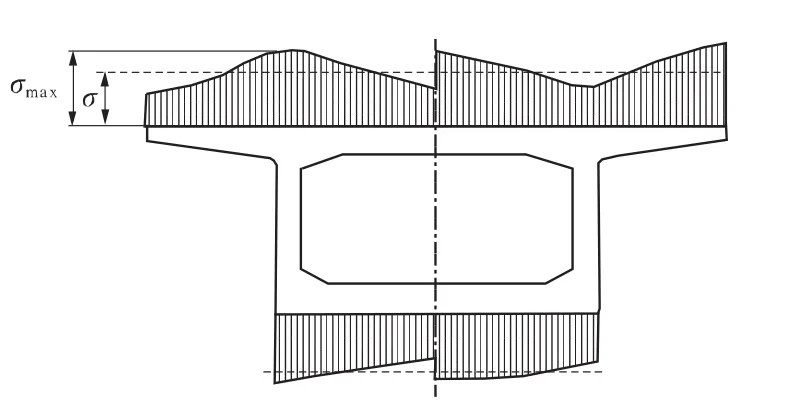
图1 箱梁正负剪力滞

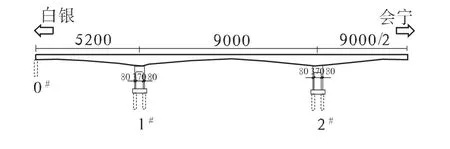
图2 靖远黄河大桥主桥一半结构立面图(单位:cm)

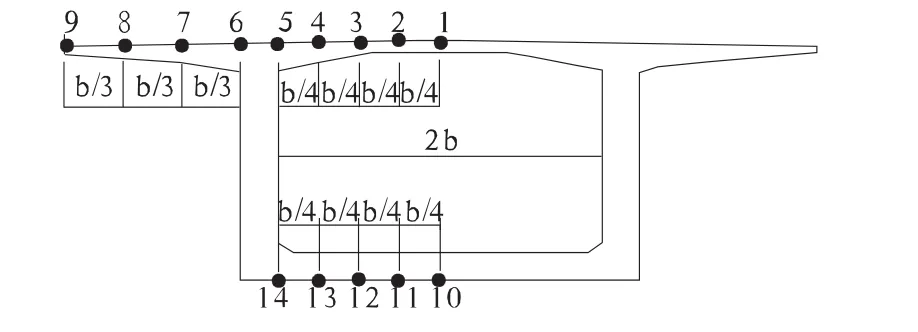
图3 横截面测点布置图

3 Ansys计算模型

Ansys计算模型见图4。

图4 靖远黄河大桥模型图

4 结果分析

自重作用下，采用有限元分析和当量法分析得到部分截面剪力滞系数，见表1。剪力滞系数图见图5、图6。

表1 自重作用下部分截面剪力滞系数

从表1中数据可得，中跨跨中截面和次边跨跨中截面处于正弯矩区，腹板和顶板、底板交界处的剪力滞系数大于1，即大于初等梁理论计算出的正应力值，越往顶板中心处或翼板远端正应力值越小，此即正剪力滞效应。比较当量截面法和Shell63及Solid65计算出来的剪力滞系数可得，对于处于正弯矩区的中跨跨中和次边跨跨中两个截面，三种方法计算出来的剪力滞系数相差较小。

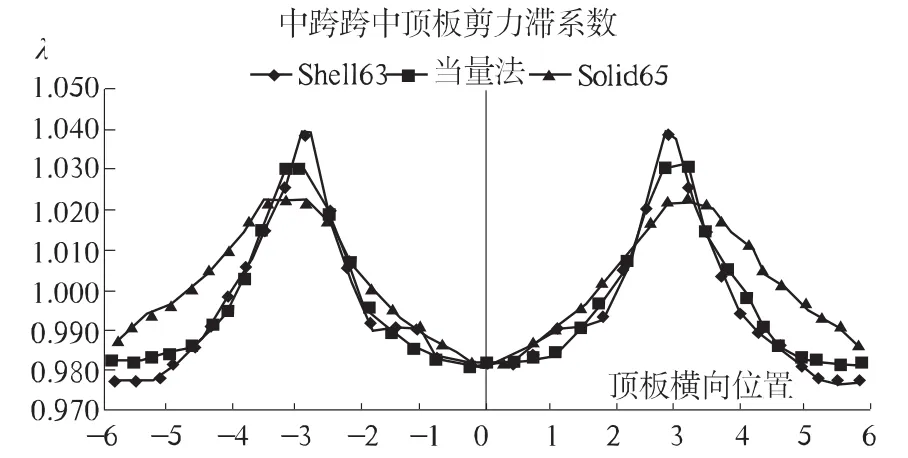
图5 中跨跨中顶板(含翼板)剪力滞系数图

图6 中跨跨中底板剪力滞系数图

从图5和图6中可以看出，采用Shell63单元计算出来的剪力滞系数在腹板和顶板交界处出现明显的峰值，而Solid65单元和当量截面法计算出来的剪力滞系数在腹板和顶板交界处有一段水平线。这个峰值是由于Shell63单元建模时的简化处理所产生的。由于Solid65单元建模时无需简化处理，基本上和桥梁实际结构相同。由于顶板和翼板并不是等厚度的板，腹板处的应力较大，而顶板和翼板与腹板交界处的梗腋加厚对腹板处的应力有减弱作用，而当量截面计算顶板与腹板交界处的剪力滞系数时是将顶板等效为等厚度的板来计算的，没有考虑梗腋对腹板应力的影响，故采用实体单元求解出来的剪力滞系数在顶板与腹板交界处比当量截面法要小。

5 结论

通过计算得出连续刚构桥的剪力滞效应有以下规律:

(1)跨径较小的边跨剪力滞效应比中跨和次边跨都要显著。

(2)超静定结构在自重荷载作用下的正弯矩区产生正剪力滞效应。

(3)边跨1/2跨附近截面发生负剪力滞效应。

［1］张士铎，邓小华，王文州.箱形薄壁梁剪力滞效应［M］.北京:人民交通出版社，1998.

［2］项海帆.高等桥梁结构理论［M］.北京:人民交通出版社，2001.

［3］周世军.箱梁的剪力滞效应分析［J］.工程力学，2008，25(2):204 －208.

［4］罗旗帜.薄壁箱形梁剪力滞计算的梁段有限元法［J］.湖南大学学报，1991(2):33－55.

［5］郭金琼.箱形梁设计理论［M］.北京:人民交通出版社，1991.

［6］陈娟.能量变分法求解箱梁剪力滞效应问题探讨［J］.桥梁研究，2007(2):88－89.