隐式Taylor级数暂态稳定计算变步长方法初探

郑焕坤，孙耀芹，常鲜戎

（1.华北电力大学 电气与电子工程学院，保定071003；2.冀北保定电力职业技术学院，保定071000）

暂态稳定算法主要有时域仿真法和直接法。直接法计算速度快，但其模型简单结果偏保守。时域仿真法利用各电气设备的数学模型，通过求解微分方程组给出变量随时间变化的曲线，计算结果准确，但其计算速度较慢。这两种方法相辅相成，在电力系统离线分析和在线安全分析中都得到广泛应用。高阶Taylor级数法是一种优秀的时域仿真法，文献［1］第一次将Taylor级数法运用到暂态稳定计算中。文献［2～4］提出快速高阶Taylor级数暂态稳定算法，并做了深入研究。文献［5，6］提出隐式Taylor级数方法，并通过调谐参数的合理设置，进一步得出了具有A稳定性的高精度隐式Taylor级数暂态稳定算法的计算格式。其中文献［6］给出具有A稳定性的高精度隐式调谐Taylor级数法。

近年来，针对时域仿真法计算速度慢的特点，提出很多改进措施。文献［8］对电力系统暂态稳定仿真和中长期稳定性仿真中的变阶、变步长技术进行了深入研究。文献［9］研究了暂态稳定仿真中的并行计算方法，以适应大规模电力系统在线实时仿真要求。文献［10］利用高阶Taylor级数法的特点，研究了快速高阶Taylor级数暂态稳定仿真方法中步长和阶数的动态控制，提高了算法的计算速度。

本文研究了隐式Taylor级数暂态稳定计算中步长的动态控制。首先对算法的计算量进行了分析，指出变步长在节省计算时间上的重要性，然后给出了误差估计方法，并在此基础上实现了变步长功能。仿真算例的结果表明：算法在采用定步长时，为取得较高的计算精度只能采用小步长，步长的减小直接导致了仿真速度的减慢；而算法在变步长时，步长的大小根据计算精度进行自动调整，既保证了计算精度又提高了计算速度。

1 算法的计算量分析

隐式Taylor级数暂态稳定算法的计算量主要集中在以下两个方面：①发电机各状态变量的各阶导数的递推求取；②形成因子表并利用它对各阶导数进行网络方程的解算。接下来针对这两个方面对算法的计算量进行分析。

在消去负荷节点和联络节点后，Taylor级数法中网络方程的导纳矩阵收缩至发电机节点，可将其看成是满阵。为了确切表示每一步求解过程的计算量，对于各状态量的m阶导数的求取均以需用的乘法次数来表示。设一个系统中包含ng个发电机节点，nf个故障节点，则由文献［11］可知形成因子表所需的计算量为

进行一次前推、回代求解网络方程的计算量为

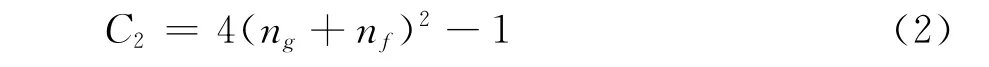
发电机各状态变量、坐标转换矩阵及诺顿电流的m阶导数的迭代求取的计算量为

对于任意m阶导数，发电机各状态变量的求解运算量为

设Taylor级数法的最高导数阶数为p＋2，由文献［2］可知实际参加求解过程为p阶，因此从0到p的各阶导数总计算量为

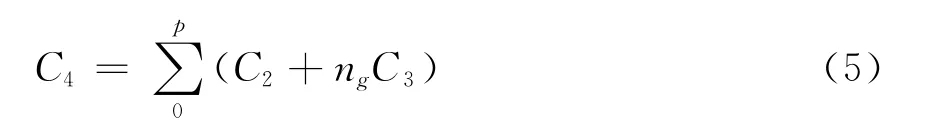
则对于每一步的计算量为

设定仿真时间T内的仿真总步数为k，每一步收敛时迭代的次数为dk，则仿真时间内总的计算量为：

由式（7）可见，仿真时间内总的计算量是总仿真步数k和每步迭代次数dk的函数。在满足精度要求的前提下，与定步长相比，变步长可使总的仿真步数减少并保证每一步的迭代次数最少，从而可减少算法的计算量，进而提高其计算速度。

2 算法的变步长控制

解微分方程的数值解法都采用“步进式”。步长对计算量和计算精度有较大影响，随着步长取值的减小，每一步截断误差会随之变小，但步数相应增加。步数的增加，不但引起计算量的增大，而且可能导致舍入误差的严重积累。变步长方法能根据计算情况对步长的大小进行自动调整，一般可起到既保证计算精度又节省计算量和计算时间的作用。

步长的自动调整需要考虑两个问题：①如何估计计算结果的精度，即给出该步的估计误差；②如何根据所估计的误差去调整步长。下面就从这两个方面介绍如何在保证计算精度的前提下，对隐式Taylor级数暂态稳定算法进行变步长控制。

2.1 误差估计

步长要实现自动调整，需要依据该步的估计误差和给定误差ε的比较来进行，而其中的误差估计是关键。在实际计算中，常采用外推法估计误差，即用同一个公式，从节点xn出发，分别用步长h计算一步，用h／2计算两步到同一节点xn＋1。然后将二者结果进行比较近似的确定误差，但是这个方法有花费时间多的弊病。

本文针对隐式Taylor级数暂态稳定算法的预估 －校正的迭代格式，提出一种新的误差估计方法，此方法与外推法相比，可节省很大的计算量。

如图1所示，其中（xk，ηk）为解曲线上的初值，F（xk，ηk）和D（xk，ηk）分别表示某数值解方向和精确解方向。以步长h计算一步产生的局部离散误差如式（8）所示。

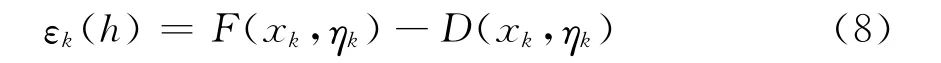
该数值方法的整体离散误差如式（9）所示。

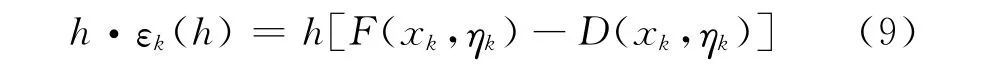
一般情况下，常微分方程的解析解很难得到。因此，精确解方向D（xk，ηk）也很难精确确定。在进行步长动态控制作用一般采用比较精确的数值解近似替代精确解方法。进而可以采用公式（9）进行误差控制。

隐式调谐Taylor级数暂态稳定算法的迭代格式及变量定义参照文献［6］。此算法是一个具有高精度及A稳定性的优秀算法，当预估式即显式Taylor级数的最高导数阶数为p阶时，相应的校正式即隐式Taylor级数可取得2p阶精度。利用隐式Taylor级数法的预估校正迭代格式及A稳定性和高精度特点，推导下述理论。

对于隐式Taylor级数暂态稳定算法的预估式，设预估式的最高导数阶数为p阶，在xk＋1处得到的数值解为y1，则有下式成立：

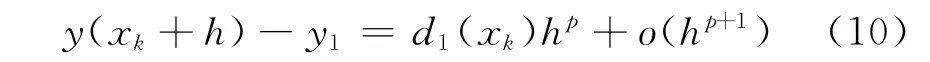
其中，d1（xk）与函数的高阶导数有关。

当预估式的最高导数阶数为p阶时，校正式的精度为2p阶，设校正式在xk＋1处得到的数值解为y2，则有下式成立：

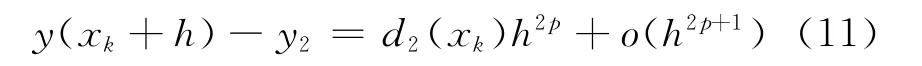
式（10）减去式（11）得

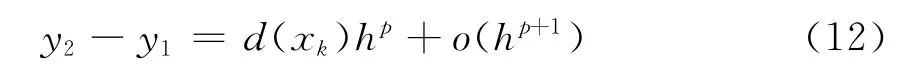
将式（12）带入式（10）得

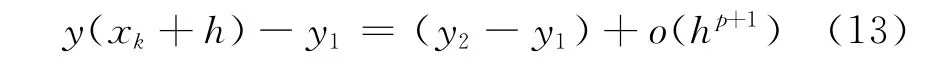
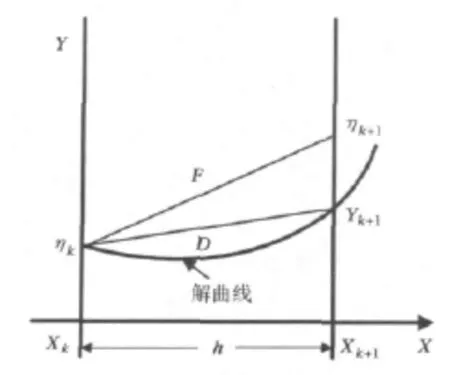
图1 局部离散误差示意图Fig.1 Schematic diagram of the local discretization error

由式（13）可见，利用预估式和校正式在xk＋1处得到的数值解的差值，可估计精确解与数值解的局部误差。与传统外推法相比，此方法充分利用了预估校正的迭代格式，不需每步都用h／2计算两步到同一节点来估计误差，从而节省了大量计算时间。

2.2 步长的动态控制

在上一节误差估计δ的基础上，依据给定的精度要求ε1和ε2即可实现步长的自动调整。

步长的调整方法通常采用加倍和折半法。但是当初始步长已经接近于合适值时，这种变步长方法将很不合理。比如，当估计误差δ比精度要求ε略小时，将步长加倍后极有可能出现δ≫ε的情况，这时不得不再将步长折半一次，回到原来的步长；同理，当估计误差δ比精度要求ε略大时，也会出现类似情况而增加后继的计算量。由于连贯性，相邻各步的合适步长的变化通常是比较平缓的，而加倍和折半处理使得步长变化过快，在整个计算过程中，这种折半和加倍的变步长方法将导致大量回退性的计算，增加计算量。因此，采用较小的步长变化量进行连续变化更加合理。当需要增加和减少步长时，本文取0.01s作为每次步长的变化量，并且配合相应的修正策略一起进行步长控制。

步长的动态控制判据如下：

1）如果δ＜ε2，则表示当前步长时该步的估计误差比精度要求小。将步长增大（可取h＝h＋0.01）进入下一步计算。

2）如果ε2＜δ＜ε1，则表示当前步长时该步的误差满足精度要求。步长保持不变，进入下一步计算。

3）如果δ＞ε1，则表示当前步长时该步的估计误差比精度要求大。将步长减小（可取h＝h－0.01），进入下一步计算。

2.3 变步长仿真中的修正策略

在程序变步长仿真过程中，为避免步长频繁切换，以加快收敛速度，本文采取如下修正策略：

（1）在仿真到网络故障时刻时，设置一个恒定步长h（可取0.01s），该步长维持到故障切除时刻，再进行可变步长的判别修改（因为此时网络的变化可能会导致故障开始时期和故障恢复初期的状态变量变化较大，从而影响到仿真速度和精度）。

（2）设置最小步长hmin（取0.005s）和最大步长hmax（取0.08s）。虽然算法具有A稳定性，但是当步长过大时可能会出现收敛困难的情况；而步长过小会使仿真步数太多，计算量增加。因此，在变步长仿真中设置最大和最小的步长限制。

3 算例分析

本文采用了忽略发电机次暂态过程的实心转子电机模型，并采用IEEEI型励磁系统。具体公式和参数详见文献［3］。

测试系统采用某省网72台发电机、432节点系统。计算机采用Intel（R）Core（TM）2Duo 2.20GHz处理器，操作系统采用Windows XP sp3。开发语言采用C＋＋，开发工具采用Visual C＋＋6.0。

仿真时间20s，设定故障为482号支路50%处（距482号支路电气距离最近的是14号发电机），5 s时发生三相短路故障，5.12s时故障消除。取仿真迭代收敛精度为10－5，各状态变量的单步误差精度要求ε1取10－5、ε2取10－6，最高导数阶数为5阶。

3.1 仿真精度对比

在定步长的情况下，程序采用不同的仿真步长时仿真精度是不一样的。本节给出了定步长时步长为0.01s和0.02s时的仿真结果，最后给出了程序在变步长时的仿真结果。

步长为0.01s时，14号发电机的转速ω仿真曲线如图2所示。

图2 定步长0.01s时，14号发电机的转速ω仿真曲线Fig.2 Simulation curve for the rotation rateωof No.14 generator at the fixed－step of 0.01s

步长为0.02s时，14号发电机的转速ω故障曲线如图3所示。

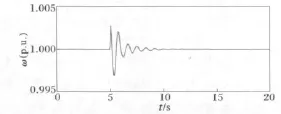
图3 定步长0.02s时，14号发电机的转速ω仿真曲线Fig.3 Simulation curve for the rotation rateωof No.14 generator at the fixed－step of 0.02s

变步长时，14号发电机的转速ω故障曲线如图4所示。

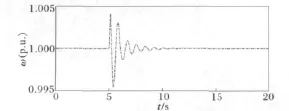
图4 变步长时，14号发电机的转速ω仿真曲线Fig.4 Simulation curve for the rotation rateωof No.14 generator at variable steps

由图2和图3可见，在定步长0.01s的仿真曲线中，最大和最小峰值分别为1.0042和0.9955，而定步长0.02s的仿真曲线的最大和最小峰值却只有1.003和0.997，并且曲线在随后的震荡过程中简化太多。这充分说明定步长0.02s的仿真精度下降。然而，由图4可见，变步长的仿真曲线和定步长0.01s时的曲线几乎完全一致，变步长可以取得类似定步长0.01s时的计算精度。在变步长仿真过程中，最小步长0.005s出现在故障后曲线震荡较剧烈的时段；最大步长0.08s出现在故障前和故障后的曲线平稳时期。

3.2 仿真速度对比

由上节可知，定步长0.02s较0.01s的仿真精度下降。而变步长可以取得定步长0.01s时较高的计算精度，并且，变步长在计算速度上也提高了很多。三种情况下的计算速度对比见表1。

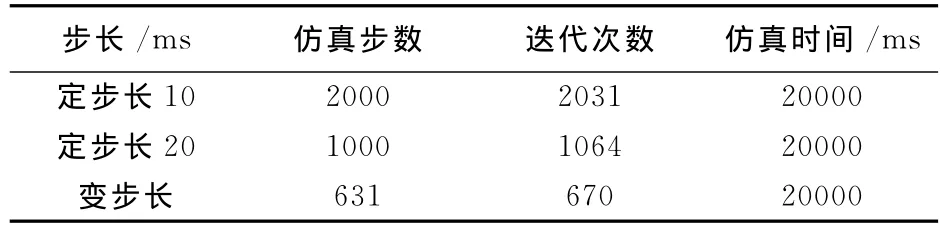
表1 定步长和变步长的总仿真步数和迭代次数对比Tab.1 Contrast of the simulation step number and the iteration number between fixed－step and variable step

从表1的仿真结果可看出，定步长0.02s较定步长0.01s在仿真速度上提高了将近一倍，但是由上节的仿真曲线对比可知，其仿真精度下降。这充分说明：算法在定步长时为了取得较高的计算精度，只能采用小步长仿真，从而不能兼顾计算速度。仿真20s，定步长0.01s需要仿真2000步，总共迭代2031次；而变步长只需要仿真631步，总共迭代670次。与定步长0.01s相比，变步长的计算速度提高了67%，显著地提高了计算效益。

4 结语

本文首先对算法的计算量进行了分析，得出步长变化与计算时间的关系，然后结合算法的预估校正迭代格式提出了一种新的误差估计方法，实现了隐式Taylor级数暂态稳定算法的变步长控制，并给出了步长修正策略。结合仿真算例，从计算精度和计算速度两个方面给出了定步长和变步长的对比结果。仿真结果表明：算法在定步长时，为了提高仿真速度而采用大步长仿真，最终导致仿真精度下降；而在变步长时，不仅保持了算法的高精度特点，同时其计算速度提高了67%，有效地提高了暂态稳定计算的效率。

［1］ Daozhi Xia，Heydt G T.On－line transient stability evaluation by system decomposition－aggregation and high order derivatives［J］.IEEE Trans on Power Apparatus and Systems，1983，102（7）：2038－2046.

［2］ 白 雪 峰，郭 志 忠，王 永 刚 （Bai Xuefeng，Guo Zhizhong，Wang Yonggang）.一种简捷快速的暂态稳定仿真算法（A new fast transient stability simulation method）［J］.继电器（Relay），2000，28（1）：1－2，45.

［3］ 郭志忠，柳焯（Guo Zhizhong，Liu Zhuo）.快速高阶Taylor级数法暂态稳定计算（Fast transient stability simulation by higher order Taylor series expansions）［J］.中国电机工程学报（Proceedings of the CSEE），1991，11（3）：8－16.

［4］ 于继来，郭志忠，柳焯（Yu Jilai，Guo Zhizhong，Liu Zhuo）.基于能量函数高阶Taylor级数展开技术的直接法（Direct method with high order Taylor series expansions of energy function）［J］.电网技 术（Power System Technology），1995，19（2）：18－20，24.

［5］ 王宇宾，常鲜戎，罗艳，等（Wang Yubin，Chang Xianrong，Luo Yan，et al）.基于隐式Taylor级数法的电力系统暂态稳定计算（An implicit Taylor series method for simulation of power system transient）［J］.华北电力大学学报（Journal of North China Electric Power University），2005，32（2）：1－6.

［6］ 郑焕坤，常鲜戎，王正辉（Zheng Huankun，Chang Xianrong，Wang Zhenghui）.高精度A稳定隐式调谐Taylor级数法在电力系统中的应用（Application of high precision and A－stability implicit tuned Taylor series method in power system）［J］.电工技术学报（Transactions of China Electrotechnical Society），2012，27（1）：217－223，230.

［7］ 邓阳，吴政球，容文光，等（Deng Yang，Wu Zhengqiu，Rong Wenguang，et al）.基于泰勒级数的N－1网络快速灵敏度修正计算（Sensitivity of N－1system fast correction calculation based on Taylor series）［J］.继电器（Relay），2007，35（16）：23－26.

［8］ 宋新立，汤涌，刘文卓，等（Song Xinli，Tang Yong，Liu Wenzhuo，et al）.电力系统全过程动态仿真的组合数值积分算法研究（Mixed numerical integral algorithm for full dynamic simulation of the power system）［J］.中国电机工程学报 （Proceedings of the CSEE），2009，29（28）：23－29.

［9］ 徐箭，陈允平（Xu Jian，Chen Yunping）.基于改进通信算法的暂态稳定并行仿真（Parallel simulation for transient stability based on improved communication algorithm in cluster environment）［J］.中国电机工程学报（Proceedings of the CSEE），2006，26（15）：12－18.

［10］ 白雪峰，郭志忠（Bai Xuefeng，Guo Zhizhong）.Taylor级数法暂态稳定计算中阶数的动态控制（The dynamic control of order selection in fast transient stability simulation by higher order Taylor series expansions）［J］.电力系统自动化（Automation of Electric Power Systems），1999，23（22）：5－7.

［11］周全仁，张清益.电网计算与程序设计［M］.长沙：湖南技术出版社，1984.

［12］黄舒予，牟龙华，石林（Huang Shuyu，Mu Longhua，Shi Lin）.自适应变步长MPPT算法（Adaptive variable step size MPPT algorithm）［J］.电 力 系 统 及其 自 动 化 学 报（Proceedings of the CSU－EPSA），2011，23（5）：26－30.

［13］ 王晨炜，靳希（Wang Chenwei，Jin Xi）.支持向量机动态训练算法电力系统暂态稳定评估（New algorithm in support vectors machine dynamic training for transient stability assessment）［J］.电 力 系 统及 其 自 动 化 学 报（Proceedings of the CSU－EPSA），2009，21（2）：31－34.

［14］ 李传栋，杨金刚，陈家荣（Li Chuandong，Yang Jingang，K.W.CHAN）.暂态稳定约束下的最优潮流（Optimal power flow with transient stability constraints）［J］.电 力 系 统 及 其 自 动 化 学 报（Proceedings of the CSU－EPSA），2009，21（6）：45－50.

［15］汪芳宗，何仰赞，陈德树（Wang Fangzong，He Yangzan，Chen Deshu）.空间时间混合变步长暂态稳定仿真新算法（Power system transient stability simulation with space－and－time varying step method）［J］.电力系统及其自动化学报（Proceedings of the CSU－EPSA），1991，3 （1）：24－30，23.