利用波形非正弦度分形估计值识别励磁涌流

文 超，黄 纯，胡 鹏，李 波

(湖南大学电气与信息工程学院，长沙 410082)

利用波形非正弦度分形估计值识别励磁涌流

文 超，黄 纯，胡 鹏，李 波

(湖南大学电气与信息工程学院，长沙 410082)

以正确鉴别变压器励磁涌流和短路电流为目的，提出一种利用波形非正弦度分形估计的电力变压器励磁涌流与内部故障电流识别方案。利用变压器励磁涌流和内部故障电流波形特征的不同，对差动电流波形进行波形非正弦度计算并分析。通过复合形态滤波算法滤除信号中的各种噪声和扰动，保证了算法的可靠性。在比较励磁涌流与短路电流波形非正弦度各自特点的基础上，提出了一种新的变压器保护方案。仿真试验结果表明：该方法能可靠识别励磁涌流与短路电流，对轻微内部故障也有较高的灵敏度。

变压器；差动保护；励磁涌流；网格分形；复合形态滤波

我国变压器保护的正确动作率长期偏低，根据相关文献统计，目前220 kV变压器差动保护正确动作率不到80%，远低于其它设备保护的运行水平，迫切需要对变压器差动保护性能做进一步改善和提高。当前差动保护的难点仍集中在励磁涌流与内部故障电流的鉴别上。现场主要采用二次谐波制动原理识别变压器励磁涌流，但随着变压器容量的不断增大，电网电压不断升高，基于二次谐波制动原理的差动保护发生误动或拒动的可能性大大提高。为提高变压器保护的可靠性，近年来，国内外学者研究了各种区分励磁涌流与内部故障电流的新方法。

文献[1]对谐波电压制动原理的灵敏性和可靠性的优缺点做了分析。文献[2～5]基于变压器励磁涌流和内部故障电流波形特征的差异提出了采样值差动原理、波形对称系数识别原理、波形相关性分析法和波形拟合法等多种励磁涌流判据。文献[6]提出利用电源侧电压和电流微分的比值来判别变压器是否含有励磁涌流。文献[7]通过检测变压器消耗有功的大小，即差有功，来识别励磁涌流。文献[8～10]分别采用等效瞬时磁阻变化特征、基于变压器数学模型的磁通对称特性等方法实现变压器保护。

网格分形算法具有简单快捷、识别准确等诸多优点，目前已成功应用于电力系统的诸多领域。将网格分形应用于变压器保护时，对采样频率没有要求，并且不需要对频段进行划分，很适合信号的实时处理。

本文通过分析差流波形网格数方差曲线的变化规律，提出了一种识别励磁涌流与故障电流的新方法。变压器正常运行或内部故障时，差动电流为正弦信号，其在半个工频周期内的网格数基本不变[11]。空载合闸出现涌流时，变压器差流严重畸变，半个工频周期内的网格数随时间变化。因此，可以通过分析网格数的变化情况来识别励磁涌流与故障电流，为避免各种噪声对该算法的影响，应用复合形态滤波算法对网格变化曲线进行平滑处理，保证算法可靠性。仿真试验验证了该方案的可行性和有效性。

1 网格分形的基本原理

对于离散化的数字信号X(采样间隔为Δ)，可以把它看成点间间距为Δ的数字点集X。设NΔ为用宽度为Δ的网格覆盖数字信号 所需的网格格子数。将覆盖数字信号X的网格宽度换为kΔ，则覆盖数字信号X所需的网格格子数为NkΔ。这样，便有k个不同网格宽度上的覆盖数字信号X所需的网格格子数NkΔ。k=1，2，…，K，其中，K充分大，使得NkΔgt;1即可。网格分形维数[12]为

1≤k≤k′≤K

(1)

其中：C为∑和式的次数。

设离散数字信号X时间段[tx-ΔT，tx]上，包含n+1(n为偶数)个采样点(x1，x2，…，xn，xn+1)，则用间距为Δ的网格覆盖该时段的信号所需要的网格格子数为

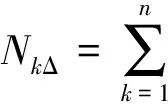
(2)

而用间距为kΔ的网格来覆盖该时段的信号所需的网格子数为

Nk′Δ=

(3)

将式(2)、(3)代入式(1)即可求得时间点tx的网格分形维数。

2 波形非正弦度分形估计

2.1 基于网格分形的算法设计

为了使分析简单化，可以不求出网格分形维数，而是基于网格数N对信号进行检测。对于一个纯正弦信号来说，如果取ΔT为半个周期，则对于任意时段ΔT，信号的网格数N值都是相同的数值。

设在时间段[tx-ΔT，tx]上，差动电流包含n+1(n为偶数)个采样点(i1，i2，…，in，in+1)。Nδ表示在时间段[tx-ΔT，tx]内以δ为边长的正方形网格覆盖信号所需的格子数，如图1所示。

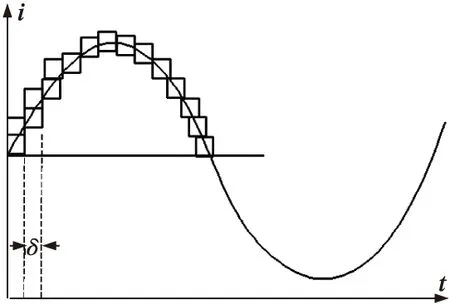
图1 网格的定义

取ΔT为半个工频周期，令δ=ΔT/n，则：

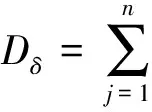
(4)

Nδ=Dδ/δ

(5)

式中：Dδ为时间段ΔT内的相邻采样点之差绝对值的求和；δ表示采样点之间的时间间隔；Nδ为时间段ΔT内的网格总数。

一般情况下，网格数Nδ是随时间变化的函数，用Nδ(t)表示。对于标准基波正弦电流，Nδ(t)是一不变的常数。Nδ(t)半周期内的数学期望可表示为

(6)

定义

(7)

式中σ[Ns(t)]为网格格数值的方差，它随着差流偏离标准基波正弦曲线的程度增大而增大。

如果差流是标准基波正弦函数，则σ[Nδ(t)]为零。σ[Nδ(t)]的大小与差流的幅值无关，只与差流波形的畸变程度有关，由此定义σ[Ns(t)]为波形非正弦度。

当变压器空载合闸或故障切除后，电压恢复过程中发生涌流时，流入继电器的差电流波形将严重畸变，则σ[Nδ(t)]很大；当变压器正常运行、内部短路或外部故障时，差流波形为近似为正弦形状，σ[Nδ(t)]很小，由此可正确区分励磁涌流和故障电流。

设σ[Nδ(t)]的门槛值σ[Nδ(t)]set，励磁涌流判据为：σ[Nδ(t)]gt;σ[Nδ(t)]set时，认为有涌流；σ[Nδ(t)]lt;σ[Nδ(t)]set时，认为无涌流。

相对于间断角原理、波形对称原理及二次谐波等涌流判别的方法，非正弦度分形估计的方法能更显著的凸显涌流的特征，并能快速制动，对变压器各种工况都具有良好的稳定性。

2.2 复合形态滤波器的设计

在现场中，变压器微机保护装置从电力系统一次侧采集的数据很容易被各种噪声和干扰污染，反映到网格变化曲线上，Nδ可能会产生波动，导致Nδ曲线极值数目增加。若此时出现内部故障，波形非正弦度也有可能大于门槛值，造成保护的误判。本文利用复合形态滤波器进行滤波，达到有效抑制噪声和抗扰动的目的。

近年来，基于数学形态学的滤波方法[13，14]以其简便易行、物理意义明确、高效实用等优点在电力系统中得到了广泛应用。其算法通常采用形态开闭运算、形态闭开运算及其组合形式等。结构元素的形状与长度的选取对形态滤波运算结果具有决定性的影响，其选取尚未有系统的方法。根据分析，最优结构元素的选取与干扰的类型和频率、待处理数据序列的采样率等因素密切相关。考虑所要鉴别的涌流特征和工程计算的要求，以及非正弦度分形估计算法自身的特点，对原始信号先进行中值滤波，再选取半圆形的结构元素，对其分别进行膨胀和腐蚀运算后取其均值。

假设x(n)为一维多值信号，B为结构元素。H和K分别为x和B的定义域。H={1，2，3，…，N}，K={1，2，3，…，M}，且Mlt;N。则离散信号x关于B的腐蚀和膨胀可定义为

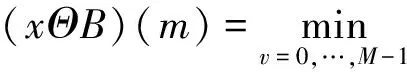
(8)

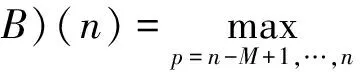
(9)

式中：v和p为满足条件的正整数；m=M-1，M，…，N-1；n=0，1，…，N-M。

3 仿真分析

利用MATLAB内置的电力系统工具箱PSB进行仿真，得到对称性励磁涌流、非对称性励磁涌流、匝间故障电流、匝地故障电流波形图。见图2～图6所示。仿真采样频率为3000 Hz，并加入噪声信号(信噪比为30 dB)。

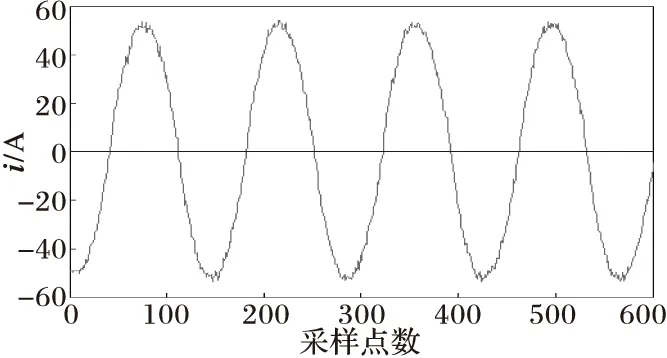
(a) 带噪声的电流波形

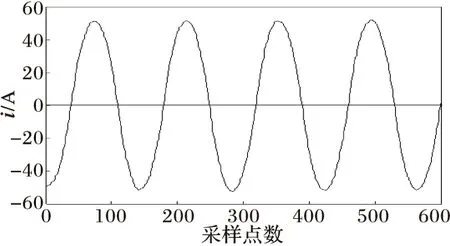
(b) 滤波处理后的电流波形

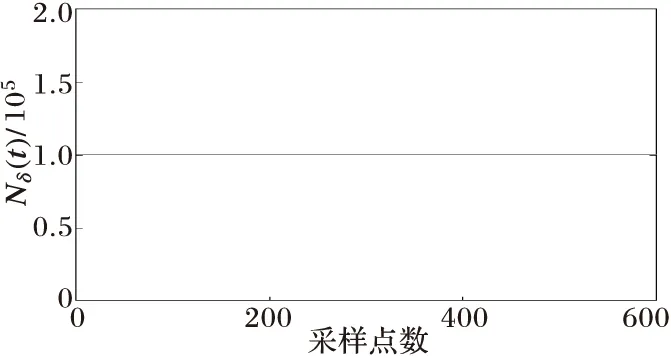
(c) 网格数变化曲线

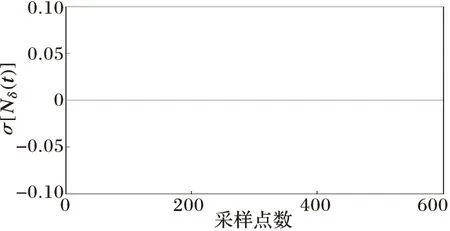
(d) 波形非正弦度变化曲线

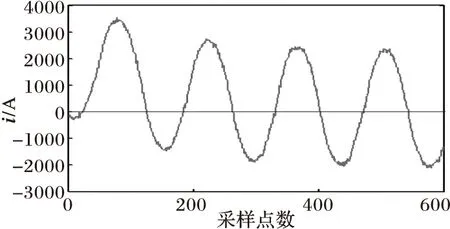
(a) 带噪声的电流波形

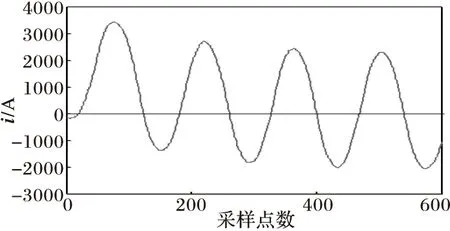
(b) 滤波处理后的电流波形

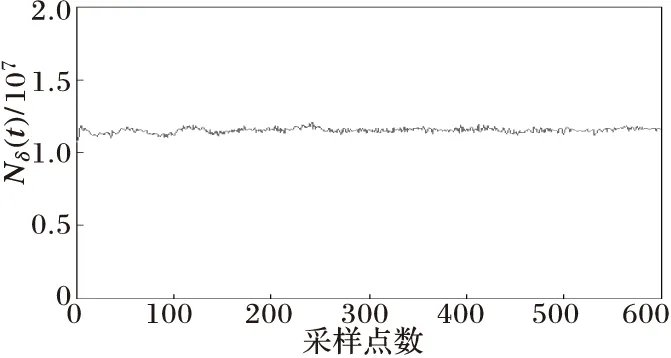
(c) 网格数变化曲线

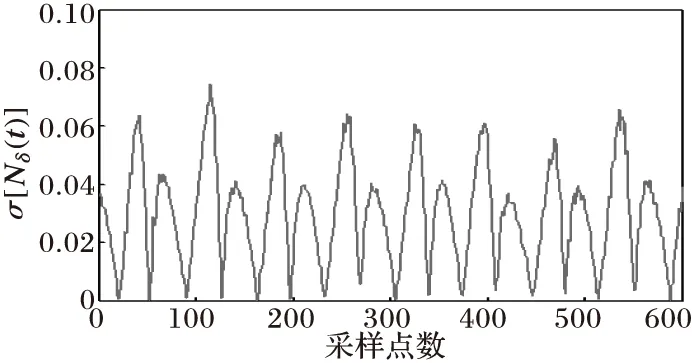
(d) 波形非正弦度变化曲线

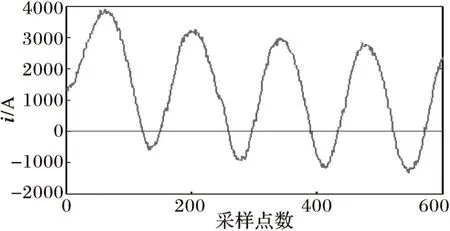
(a) 带噪声的电流波形

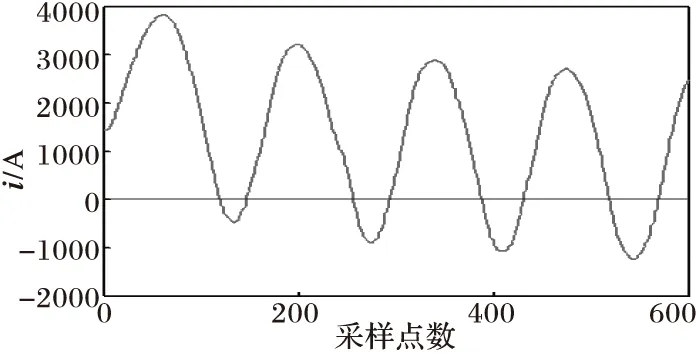
(b) 滤波处理后的电流波形

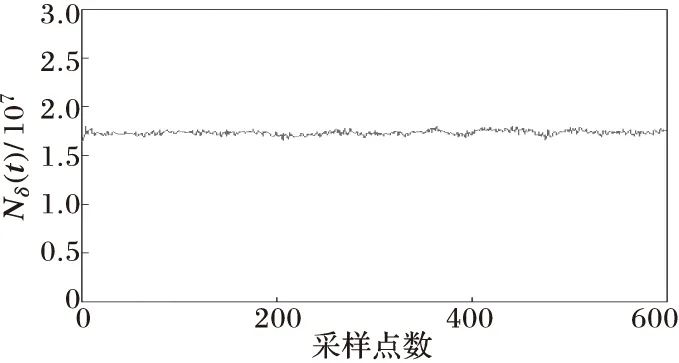
(c) 网格数变化曲线

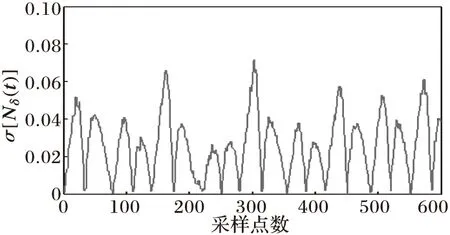
(d) 波形非正弦度变化曲线

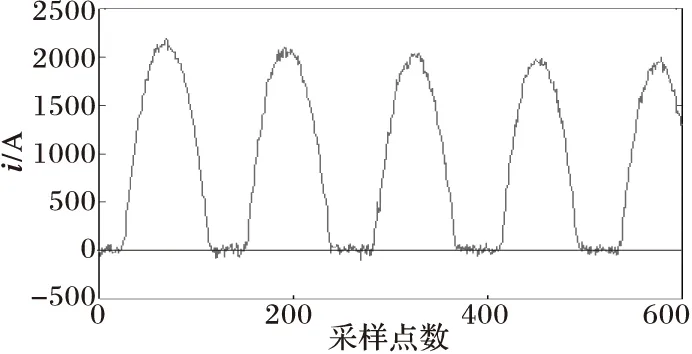
(a) 带噪声的电流波形

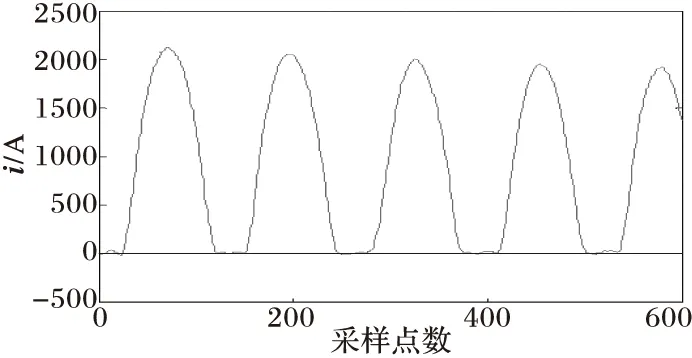
(b) 滤波处理后的电流波形

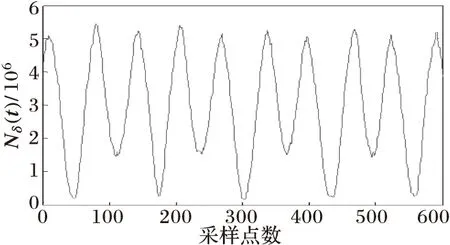
(c) 网格数变化曲线

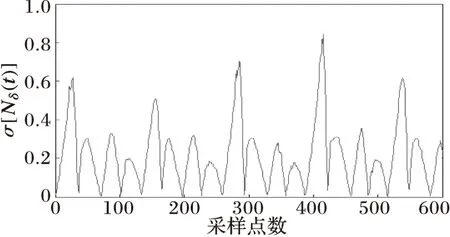
(d) 波形非正弦度变化曲线

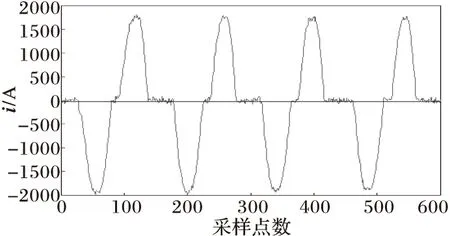
(a) 带噪声的电流波形

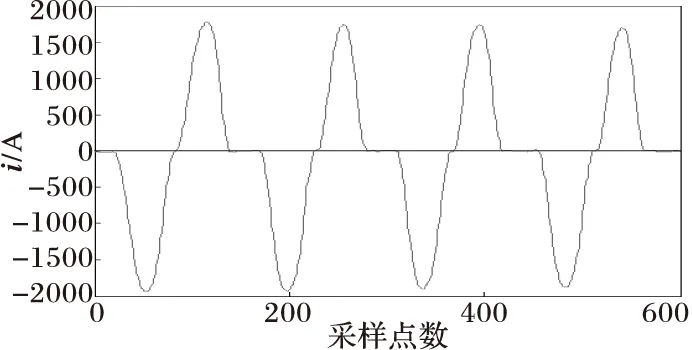
(b) 滤波处理后的电流波形

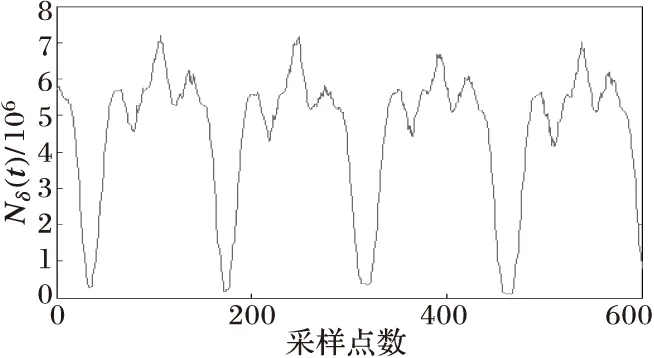
(c) 网格数变化曲线

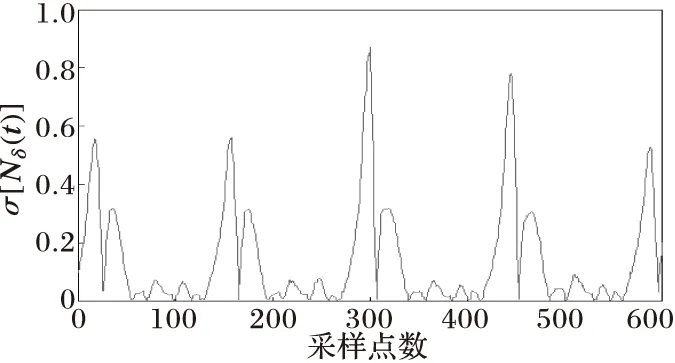
(d) 波形非正弦度变化曲线

图3匝间短路与图4匝地短路的情况下，变压器电流波形近似为正弦波形，从网格数变化曲线可以看出内部故障电流有轻微的畸变，导致网格曲线发生波动，而波形非正弦度σ[Nδ(t)]的数值很小，远未超过0.1。

图5与图6分别为当变压器发生非对称性涌流和对称性涌流时的情况，可以看出变压器电流波形具有间断角和尖顶波的明显特征，从网格数变化曲线可以看出Nδ(t)值变化剧烈，当变压器铁心进、退饱和时，网格数Nδ(t)将出现极小值和极大值点。由于涌流波形畸变严重，涌流波形的非正弦度σ[Nδ(t)]的极值会很大，远超过0.1。

综合上面各仿真波形可以发现，故障电流波形的非正弦度值远小于0.1，而涌流波形的非正弦度极值远大于0.1。

可设定阈值σ[Nδ(t)]set=0.1，当一周期内至少有一个点的σ[Nδ(t)]set值大于0.1值时则判断为涌流；当一周期内所有点的σ[Nδ(t)]值都小于0.1时则判断为内部故障电流。

根据此判据和图中仿真结果可知：此算法可迅速可靠地区分涌流和内部故障电流。

4 结语

本文利用变压器励磁涌流与故障电流在网格曲线特征上的差异，提出了波形非正弦的概念，并以此为基础提出了一种有效识别励磁涌流和内部故障电流的新方法。

此方法利用变压器在进入饱和点和退出饱和点时σ[Nδ(t)]值明显大于其他点的σ[Nδ(t)]的特征，对励磁涌流进行准确识别，针对网格分形曲线容易受噪声影响的特点，设计了复合形态滤波器，防止噪声对本算法的影响。

仿真结果表明：该方法能快速、准确地识别变压器励磁涌流和内部故障电流。

[1]Thorp J S,Phadke A G.A microprocessor based voltage restraint three phase transformer differential relay[J].Proceeding of the South Eastern Symposium on System Theory,1984,18(4):312-316．

[2]胡玉峰，陈德树(Hu Yufeng,Chen Deshu).基于采样值差动的励磁涌流鉴别方法(A new method to identify inrush current based on sampled values)[J].中国电机工程学报(Proceedings of the CSEE)，2000，20(9)：55-58，63．

[3]姚斌，李永丽(Yao Bin，Li Yongli).基于波形上下对称系数识别励磁涌流的新原理(Novel theory of identifying inrush current based on waveform longitudinal symmetry)[J]．电力系统及其自动化学报(Proceeding of the CSU-EPSA)，2004，16(2)：32-35．

[4]李贵存，刘万顺，腾林，等(Li Guicun,Liu Wanshun,Teng Lin,etal).基于波形相关性分析的变压器励磁涌流识别新算法(A new algorithm of discrimination between inrush current and fault current of transformer based on self-correlation analysis)[J].电力系统自动化(Automation of Electric Power Systems)，2001，25(17)：25-28．

[5]李贵存，刘万顺，刘建飞，等(Li Guicun,Liu Wanshun,Liu Jianfei,etal).用波形拟合法识别变压器励磁涌流和短路电流的新原理(New principle of discrimination between inrush current and fault current of the transformer based on forecasted waveform)[J].电力系统自动化(Automation of Electric Power Systems)，2001，25(14)：15-18．

[6]徐岩，王增平，杨奇逊，等(Xu Yan,Wang Zengping,Yang Qixun,etal).基于电压电流微分波形特性的变压器保护新原理的研究(Research on novel transformer protection based on the characteristics of voltage and differential current)[J].中国电机工程学报(Proceedings of the CSEE)，2004，24(2)：61-65．

[7]Yabe K.Power differential method for discrimination between fault and magnetizing inrush current in transformers[J].IEEE Trans on Power Delivery，1997，12(3)：1109-1118．

[8]刘玉欢，陆于平，林霞，等(Liu Yuhuan,Lu Yuping，Lin Xia,etal).基于磁制动原理的特高压变压器励磁涌流快速识别(A novel scheme based on flux restraint theory used in distinguishing inrush currents for UHV transformers)[J].中国电机工程学报(Proceedings of the CSEE)，2007,27(34):52-58．

[9]张雪松，何奔腾(Zhang Xuesong,He Benteng).基于误差估计的变压器励磁涌流识别原理(A new method identify inrush current based on estimation)[J].中国电机工程学报(Proceedings of the CSEE)，2005，25(3)：94-99．

[10]赵永彬，陆于平(Zhao Yongbin,Lu Yuping).基于磁通对称特性的变压器励磁涌流判别新算法(A new algorithm based on flux symmetry character for judging transformer inrush current)[J].电工技术学报(Transactions of China Electrotechnical Society)，2007,22(12):66-71．

[11]王曾平，马静(Wang Zengping，Ma Jing).基于网格分形的励磁涌流识别新方法(A novel method to identify inrush current based on grille fractal)[J].电网技术(Power System Technology)，2007,31(11):63-68．

[12]吴敏金.分形信息导论[M].上海:上海科学技术文献出版社，1994．

[13]吴青华,张东江(Wu Qinghua，Zhang Dongjiang).形态滤波技术及其在继电保护中的应用(Morphological filtering techniques and applications in protection relaying)[J].电力系统自动化(Automation of Electric Power Systems)，2003,27(7):45-49．

[14]陈平,李庆民(Chen Ping，Li Qingmin).基于数学形态学的数字滤波器设计与分析(Design and analysis of mathematical morphology-based digital filters)[J].中国电机工程学报(Proceedings of the CSEE)，2005,25(11):60-65．

文 超(1987-)，男，硕士研究生，研究方向为电力系统继电保护。Email:superpippo619@163.com

黄 纯(1966-)，男，教授，博士生导师，研究方向为电力系统自动化、电能质量分析与控制。Email:yellowpure@21cn.com

胡 鹏(1981-)，男，工程师，研究方向为发电厂运行与控制。Email:starhp@126.com

IdentificationofTransformerInrushCurrentbyUsingofFractalEvaluationofWaveformNon-SinusoidalLevel

WEN Chao，HUANG Chun，HU Peng，LI Bo

(College of Electrical and Information Engineering,Hunan University,Changsha 410082,China)

Taking the correct identification of Transformer inrush current and fault current as objective,a novel scheme to identify inrush current and internal fault current by comparing the non-sinusoidal level fractal evaluation of waveform is proposed in this paper.Based on the different waveform characteristics between inrush current and internal fault current,the non-sinusoidal level of differential current waveform is calculated and analyzed.To ensure the reliability of the grille fractal,the complex morphological filter is used to filtrate the noises and interference signals.On the basis of comparing the feature of inrush and fault current waveform of non-sinusoidal level value,a novel transformer protection scheme is proposed.The simulation tests show that the proposed method can identify inrush current rapidly and reliably,and still keeps good sensibility even in the case of slight internal fault.

transformer；differential protection；inrush current；grille fractal；complex morphological filter

TM772

A

1003-8930(2012)04-0071-06

2010-12-20；

2011-03-09