基于轨迹灵敏度分析的直流调制参数优化设计

王长香，房大中，薛振宇，魏文辉

(1.天津大学电气与自动化工程学院，天津 300072；2.中国电力科学研究院，北京 100192)

基于轨迹灵敏度分析的直流调制参数优化设计

王长香1，房大中1，薛振宇1，魏文辉2

(1.天津大学电气与自动化工程学院，天津 300072；2.中国电力科学研究院，北京 100192)

提出一种基于时域仿真的直流调制参数优化方法，将直流调制参数优化问题转化为带参数约束的非线性优化问题。该方法，首先将约束优化问题转化为无约束优化问题，通过轨迹灵敏度仿真得到目标函数的梯度信息，应用拟牛顿法(DFP)优化直流调制控制器参数。由于目标函数反映了AC/DC复杂系统的动力学特性，该方法可有效地改善系统的阻尼特性，抑制大扰动引起的系统振荡。在IEEE四机系统上进行的特征值分析和时域仿真结果验证了该方法的有效性和鲁棒性。

直流调制；轨迹灵敏度；拟牛顿法；参数优化

直流输电功率调节快速灵活，不像交流系统存在同步稳定性问题，是较理想的大容量远距离输电方式。

文献[1]中指出直流系统常规控制方式虽然可以缓冲一侧交流系统对另一侧交流系统的扰动，但由于换流器像是一个对频率不敏感的负荷，不但不会为发电机提供同步转矩，反而会为发电机提供负的阻尼转矩，不利于系统的稳定。因此，为了提高交流系统的动态稳定性，常须装附加阻尼控制来拓展直流系统的可控性。

为了提高交流系统的机电振荡阻尼，抑制大扰动引起的系统振荡，可以在直流系统控制器上附加阻尼控制器，即直流调制[2，3]。采用直流调制的一个典型例子是美国太平洋联络线[4]，该工程采用小信号电流调制来抑制并联交流线路上的功率振荡。文献[5]采用整流侧的直流功率调制和逆变侧的熄弧角调制来阻尼并联交流线路上的区间低频振荡，取得了很好的控制效果。文献[6，7]对直流调制改善南方电网交直流并联系统稳定性进行了研究，研究表明直流调制可有效改善交直流并联系统的稳定性，快速抑制交流系统功率振荡。但是，文献[5，6，7]中采用的直流调制参数都是来源于工程经验或大量仿真计算确定，因为实际交直流并联系统具有结构复杂、动态特性很难精确描述的特点。只有合理配置直流调制参数，才能有效改善系统阻尼，抑制系统功率振荡，因此大规模AC/DC复杂系统的直流调制参数整定仍然是一个重要的研究课题。

长期以来，学者们对直流调制控制器参数优化问题进行了大量的研究，并提出了多种优化方法，这些方法已在实际应用中取得了一定的效果[8～12]。近年来，遗传算法、模拟退化算法、混沌优化算法等智能优化算法已经广泛应用到参数优化中，文献[9]和[11]提出了基于混沌优化算法的直流调制控制器参数优化算法，并通过中国南方电网和三区域双馈入交直流系统进行了验证。然而，智能优化算法普遍具有随机性强、收敛速度慢的缺点。文献[8]和[10]对南方交直流混合电网直流调制的参数协调优化问题进行了研究，也取得了很好的效果。文献[13]提出了一种基于轨迹灵敏度优化电力系统稳定器参数的方法，并通过新英格兰系统和四机系统进行验证。

将文献[13]的思想应用到直流调制控制器参数优化中，提出了一种基于轨迹灵敏度分析的直流调制控制器参数优化方法。该方法通过时域仿真得到系统的轨迹和轨迹灵敏度，继而得到目标函数的梯度信息，应用拟牛顿法(DFP)优化直流调制控制器参数。由于该方法目标函数反映了AC/DC复杂系统的动力学特性，该方法设计的直流调制控制器，不仅可提高小扰动稳定性，还可有效抑制大扰动后的系统振荡。在IEEE四机系统上进行的特征值分析和时域仿真结果验证了该方法的有效性和鲁棒性。

1 AC/DC系统数学模型

1.1AC/DC系统机电暂态仿真的基本原理

为了更准确地反映直流系统中元件的动态性能对交流系统稳定性的影响，在AC/DC系统机电暂态仿真中，使用较为精确的直流输电模型，即准稳态模型[14]。在准稳态模型中，换流器方程仍用直流分量有效值与基频交流分量之间的关系表示，直流线路用R-L线路模拟。

在AC/DC系统机电暂态仿真中，交流系统和直流系统是相互作用的，如图1所示。对直流线路来说，两侧的换流器相当于两个电压源，其数值决定于触发控制角和交流侧换流母线电压有效值。对交流系统来说，直流系统相当于一个变化的负荷，可用挂在换流站交流母线上的可变功率支路来模拟。

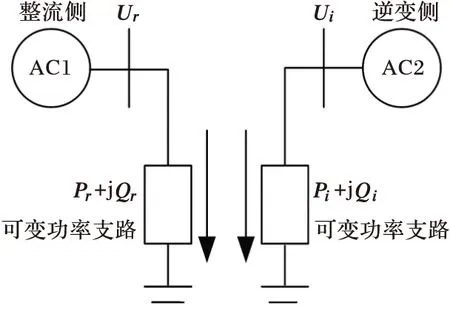
图1 AC/DC系统相互作用示意图

1.2 直流控制器模型及直流调制模型

对于直流控制系统，本文采用整流侧定电流控制，逆变侧定熄弧角控制的调节运行方式，直流控制器采用文献[14]中给出的控制器模型，定电流控制器及直流调制模型如图2。

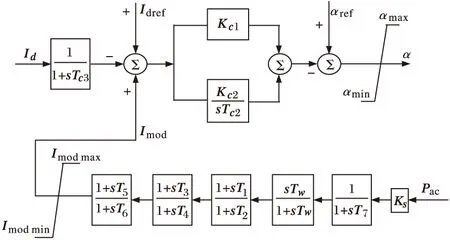
图2 直流控制器及直流调制模型

直流调制以与直流并联交流联络线传输的有功功率Pac作为输入信号，经过测量、隔直和超前滞后环节，再经过限幅环节后得到电流调制信号Imod，Imod和电流控制信号Idref进行综合，经过定电流控制器控制整流侧触发角α，从而控制直流线路传输功率，达到改善系统稳定性的目的。

图2中，对于定电流控制器，Id和Idref分别为输入信号和电流控制信号；Tc3为测量环节时间常数；Kc2和Tc2分别为积分环节增益系数和时间常数；Kc1为比例环节增益系数；αref为整流侧触发角参考值。对于直流调制控制器，Ks为增益系数；T7和Tw分别为测量环节和隔直环节时间常数；T1、T2、T3、T4、T5、T6为超前滞后环节的时间常数。下标max和min分别表示相应变量的上下限值。图中除角度和时间外，其它所有变量和参数均为标幺值。

1.3 电力系统暂态模型

AC/DC混联电力系统的非线性模型由发电机及其控制器、负荷和HVDC及其他装置模型组成，并通过网络方程连接，其动态过程可用如下一般形式的微分-代数方程组表示：

(1)

式中：微分方程组f(·)描述各动态元件的动态特性，包括发电机及其控制系统、直流线路和直流控制器等动态元件；代数方程组g(·)包括网络方程、各动态元件与网络接口方程、HVDC电压方程等；向量x表示状态变量；向量y表示运行参量；α表示待优化参数向量；x0、y0表示状态变量和运行参量的初值，由潮流计算确定。

2 直流调制参数优化设计

2.1 直流调制参数优化问题模型

优化直流调制控制器参数的目的是改善系统的阻尼特性，抑制系统区域间的低频振荡，使得电力系统以最快的速度恢复到稳定运行点。本文采用系统中发电机的速度偏差构成二次型性能指标如下：

(2)

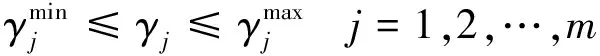
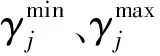
式(2)所表示性能指标的物理意义如图3所示，显而易见，系统发电机速度偏差平方的积分为图中阴影部分的面积，面积越小则系统振荡平息的越快，也就是说系统的阻尼特性越好。因此，最小化性能指标(2)，系统振荡的阻尼被最大化，此时对应的参数为直流调制控制器的最优参数。

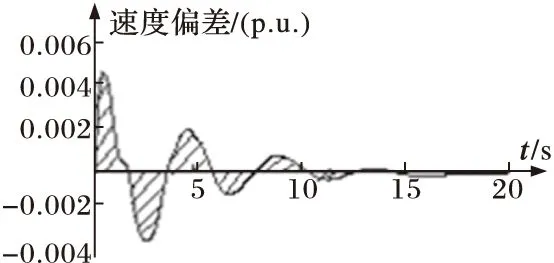
图3 目标函数的物理意义

直流调制参数优化问题模型式(2)是一个有约束非线性优化问题，其一般解决方法是先转化为无约束优化问题。引入非线性变换[13，15]：

(3)

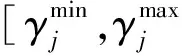
minJ(X)

(4)

2.2 轨迹灵敏度分析

运用轨迹灵敏度方法可定量分析电力系统某些参数对其动态性能的影响，在电力系统参数辨识、电力系统稳定分析与控制以及附加阻尼控制器的参数设置等领域都得到了广泛的应用。本文仅对轨迹灵敏度作简单介绍，具体参见文献[15]。对式(1)求偏导数可得：

(5)

式中：xα(t)和yα(t)分别表示状态变量x和运行参量y对直流调制控制器参数的灵敏度；fx、fy和fα分别表示f对向量x、y和α的梯度；gx、gy和gα具有相同意义。本文称式(1)为轨迹系统，其伴随系统式(5)被称为轨迹灵敏度系统。运用双向模块简化技术联合求解轨迹和轨迹灵敏度系统，可大大减少轨迹灵敏度系统的计算量[8]。

采用拟牛顿法求解式(4)的无约束优化问题的前提是要获得目标函数的梯度信息。通过时域仿真计算得到每一时步的ωi和ω(rj)i，将其带入式(6)，从而可得到目标函数的梯度信息∂J/∂X=[∂J/∂β1，∂J/∂β2，…，∂J/∂βm]T。目标函数对任意变量βj的导数表达式如下：

(6)

式中：ω(γj)i表示第i台发电机相对同步坐标的速度偏差对第j个待优化参数γj的轨迹灵敏度；其它变量的含义，上文已作介绍，这里不再赘述。

2.3 优化算法简介

直流调制控制器参数优化过程：首先给定一组初始参数及收敛条件，进行时域仿真得到系统的轨迹和轨迹灵敏度，利用拟牛顿法优化直流调制参数，直到满足收敛条件，得到最优参数为止。采用VS2005编写程序，实现本文所提算法。图4为程序基本流程图。

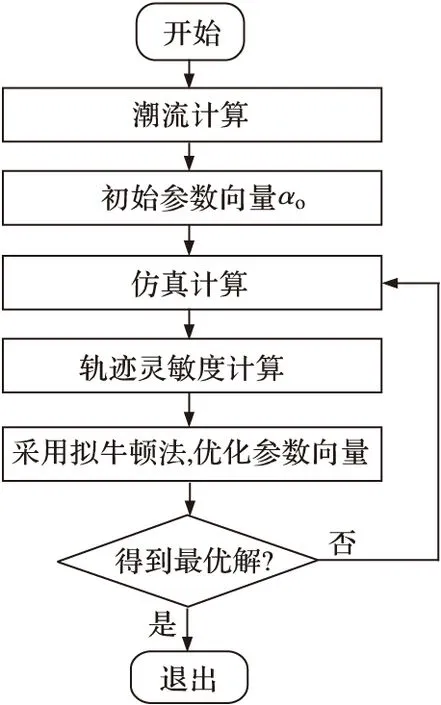
图4 直流调制参数优化流程图

本文采用拟牛顿法(DFP)[16]求解直流调制控制器参数优化问题。拟牛顿法的基本思想是用一阶导数近似得到海森矩阵的逆矩阵，不必计算二阶导数，减少了计算量。同时综合了最速下降法具有较好的整体收敛性和牛顿法收敛速度快的优点。DFP算法是第一个被提出的拟牛顿算法，也是无约束最优化问题最有效的算法之一。

DFP算法步骤：

步骤1给定控制误差ε，给定直流调制控制器的初始参数α0，通过式(3)的非线性变换得到初始点X0，给定初始矩阵H0(通常取单位矩阵E)，计算初始梯度g0，令k=0。

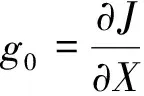
(7)

步骤2令k步的搜索方向pk。

pk= -Hkgk

(8)

步骤3由精确一维搜索确定步长λk。

(9)

步骤4计算Xk+1，由式(3)计算得到αk+1。

Xk+1=Xk+λkpk

(10)

步骤5将αk+1带入轨迹灵敏度系统，计算k+1步的梯度gk+1，若满足‖gk+1‖≤ε，则最优解X*=Xk+1；否则令

sk=Xk+1-Xk，yk=gk+1-gk

(11)

步骤6由DEP修正公式计算Hk+1。令k=k+1，转到步骤2。

(12)

3 算例分析

图5为IEEE四机系统的结构图，系统参数见文献[1]。算例中：系统功率基准值为100 MVA；发电机均采用双轴暂态模型，每台发电机配有EA模型的励磁器；负荷采用恒阻抗负荷；两端直流输电系统采用准稳态模型，控制系统采用整流侧定电流，逆变侧定熄弧角调节运行方式，直流控制器及直流调制模型见图2。直流调制输出信号上下限Imod max和Imod min分别为0.3Ids(p.u.)和-0.2Ids(p.u.)，其中Ids为给定直流线路电流标幺值。定电流控制器参数取值为：Tc3=0.09，Kc1=0.75，Kc2=10，Tc2=1。对于直流调制控制器[1]，Tw一般取经验值，Tw=10，由于本文主要考虑抑制区域间低频振荡，这个数值可以避免低频时产生较大的相位超前，而破坏区域间暂态稳定性；测量环节时间常数T7=0.01；滞后时间常数T2=T4=T6=0.2；超前时间常数T1、T3、T5为待优化参数，考虑到实际情况，每个超前或滞后环节补偿量限于最大值60°，其取值范围为[0.01，5.0]；增益Ks为待优化参数，其取值范围为[0.01，2.0]。

参数优化采用的预想故障为L7-8在母线7侧发生三相短路，0.2 s故障，经5个周波0.3 s故障消失。应用本文方法优化后的直流调制控制器参数列于表1，其对应系统机电振荡模式特征值列于表2。表2中还列出了无直流调制控制器系统的机电振荡模式特征值。由表2可见，没有安装直流调制控制器，系统机电模式最小阻尼比为0.017，一般要求机电模式最小阻尼比不小于5%，故系统阻尼较弱。而安装本文设计的直流调制控制器后，系统机电模式特征值明显向复平面左平面大幅移动，提高了系统机电模式阻尼特性，可有效抑制系统的低频振荡。

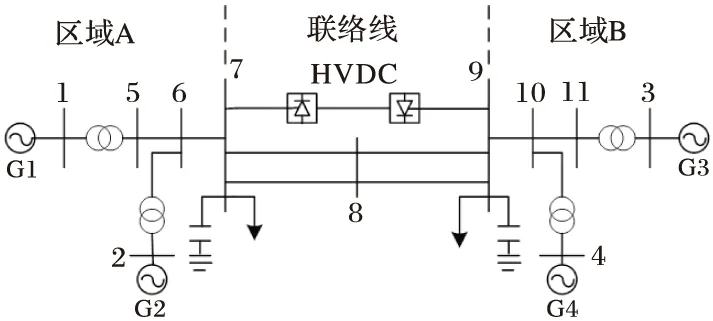
图5 IEEE四机算例系统

表1 直流调制参数

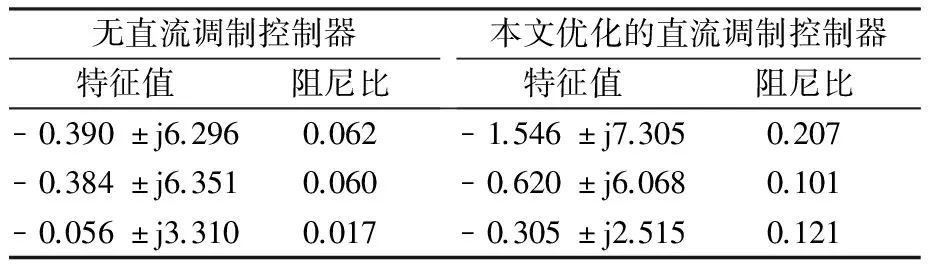
表2 IEEE四机算例系统机电振荡模式特征根比较

在上述故障条件下，分别对无直流调制控制器、直流调制控制器采用预选参数和本文优化后参数的三种情况进行时域仿真，仿真结果如图6～7。由图6～7可见，本文优化设计的直流调制控制器可以有效提高系统的阻尼特性，抑制大扰动后的系统振荡，使得故障后系统发电机的功角快速衰减，系统功率振荡得到快速抑制。

图6 1号发电机相对4号发电机的功角摇摆曲线

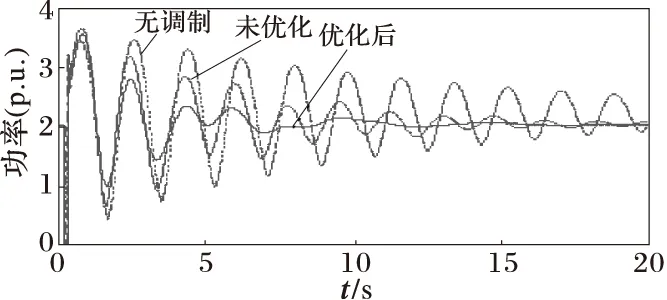
图7 交流联络线L7-8有功功率振荡曲线

直流调制控制器参数优化设计方法的一个重要要求是鲁棒性，优化结果应确保直流调制在系统运行方式或系统结构发生变化后，仍然可以有效抑制系统振荡。上面已经说明了L7-8线路三相短路故障经5个周波后消失，优化参数对抑制系统振荡的良好效果。直流调制控制器采用优化后参数分别对以下两种情况进行时域仿真，验证本文优化方法的鲁棒性。

(1)图5系统中，L8-9的一回线路在母线8侧发生三相短路，0.2 s时故障，经5个周波0.3 s切除一条线路。仿真结果如图8，验证了该优化方法对系统结构改变具有一定的鲁棒性。

(2)图5系统中，改变系统运行方式，交流联络线L7-8双回线的输送功率由201.6 MW增加到298.2 MW，故障取L7-8线路0.2 s在母线7侧三相短路经5个周波后故障消失。仿真结果如图9，验证了本文优化方法对系统运行方式改变具有一定的鲁棒性。

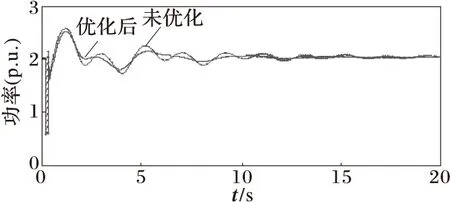
图8 交流联络线L7-8有功功率振荡曲线

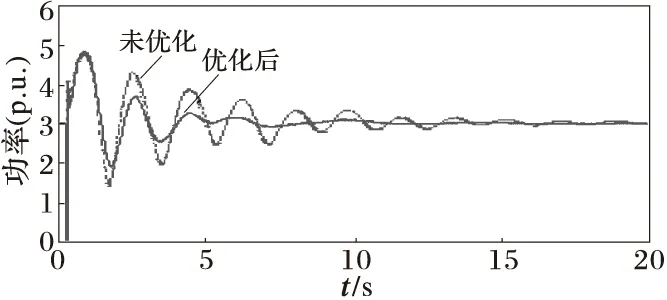
图9 交流联络线L7-8有功功率振荡曲线

4 结语

本文提出了一种基于时域仿真的直流调制参数优化方法，优化后的直流调制控制器可以有效提高系统整体的阻尼特性，抑制系统振荡，使得系统快速恢复到稳定运行状态。通过在IEEE四机系统上的特征值分析和时域仿真结果，验证了该方法的有效性和鲁棒性。将本文提出方法应用到实际复杂电力系统是进一步要研究的重点。

[1]Kundar P.Power System Stability and Control[M].New York:McGraw-Hill,1994.

[2]Peterson H A,Krause P C.Damping of power swing in a parallel AC and DC system [J].IEEE Trans on Power Apparatus and Systems,1966,85(12):1231-1239．

[3]徐政.交直流电力系统动态行为分析[M].北京:机械工业出版社，2004.

[4]Cresap R L，Scott D N，Mittelstadt W A．Small-signal modulation of the Pacific HVDC Inter-tie[J]．IEEE Trans on Power Apparatus and Systems，1976，95(2)：536-541．

[5]沈梁，陈陈，史慧杰，等(Shen Liang,Chen Chen,Shi Huijie,etal).直流调制对电网区间低频振荡的抑制作用(Suppression of inter-area low frequency oscillation by HVDC modulation)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA)，2008，20(4)：82-86．

[6]荆勇，洪潮，杨晋柏，等(Jing Yong,Hong Chao,Yang Jinbai,etal).直流调制抑制南方电网区域功率振荡的研究(Suppression of inter-area power oscillation in southern China power grid by HVDC modulation)[J].电网技术(Power System Technology)，2005，29(20)：53-56．

[7]荆勇，杨晋柏，李柏青，等(Jing Yong,Yang Jinbai,Li Baiqing,etal).直流调制改善交直流混联系统暂态稳定性的研究(Research on improving transient stability of AC/DC hybrid system by HVDC modulation)[J].电网技术(Power System Technology)，2004，28(10)：1-4．

[8]刘红超，李兴源，王路，等(Liu Hongchao,Li Xingyuan,Wang Lu,etal).多馈入直流输电系统中直流调制的协调优化(Coordination and optimization of HVDC modulations in multi-infeed HVDC transmission system)[J].电网技术(Power System Technology)，2004，28(1)：5-9．

[9]郑希云，李兴源，王渝红(Zheng Xiyun,Li Xingyuan,Wang Yuhong).基于混沌优化算法的PSS和直流调制的协调优化(Coordination and optimization of PSS and HVDC modulations using chaotic optimization algorithm)[J].电工技术学报(Transactions of China Electrotechnical Society)，2010，25(5)：170-175．

[10]毛晓明，张尧，管霖，等(Mao Xiaoming,Zhang Yao,Guan Lin,etal)．南方交直流混合电网区域振荡的协调控制策略(Research on coordinated control strategy for inter-area oscillations in China southern AC/DC power grid)[J].电力系统自动化(Automation of Electric Power Systems)，2005，29(20)：55-59．

[11]周孝法，陈陈，杨帆，等(Zhou Xiaofa,Chen Chen,Yang Fan,etal).基于自适应混沌粒子群优化算法的多馈入直流输电系统优化协调直流调制(Optima coordinated HVDC modulation based on adaptive chaos particle swarm optimization algorithm in multi-infeed HVDC transmission system)[J].电工技术学报(Transactions of China Electrotechnical Society)，2009，24(4)：193-201.

[12]金丽成，刘海峰，徐政(Jin Licheng,Liu Haifeng,Xu Zheng).多馈入直流输电系统小信号调制器的协调优化整定(Coordination and optimization of small signal modulation in multi-infeed HVDC systems)[J].电力系统自动化(Automation of Electric Power Systems)，2003，27(16)：10-15．

[13]周保荣，房大中，孙景强(Zhou Baorong,Fang Dazhong,Sun Jingqiang).基于轨迹灵敏度分析的电力系统稳定器参数优化设计(Tuning of PSS parameters using optimization approach based on trajectory sensitivity analysis)[J].电网技术(Power System Technology)，2004，28(19)：20-23,84．

[14]王锡凡,方万良,杜正春.现代电力系统分析[M].北京:科学出版社，2003.

[15]Hiskens Ian A,Pai M A.Trajectory sensitivity analysis of hybrid systems [J].IEEE Trans on Circuits and Systems,2000,47(2):204-220.

[16]解可新,韩健,林友联.最优化方法[M].天津:天津大学出版社，1997.

王长香(1986-)，女，硕士研究生，研究方向为电力系统稳定性。Email:daisywang_415@yahoo.cn

房大中(1946-)，男，教授，博士生导师，主要从事电力系统稳定性分析与控制研究。Email:dz_fang@yahoo.com.cn

薛振宇(1983-)，男，博士研究生，研究方向为电力系统安全分析和数据库等。Email:banditxue@163.com

ParameterOptimizationDesignofDCModulationBasedonTrajectorySensitivityAnalysis

WANG Chang-xiang1，FANG Da-zhong1，XUE Zhen-yu1，WEI Wen-hui2

(1.School of Electrical Engineering and Automation，Tianjin University，Tianjin 300072，China；2.China Electric Power Research Institute，Beijing 100192，China)

A method for parameter-optimization of DC-modulation controller on the basis of time domain simulation has been proposed in this paper.In this method,the parameter optimization problem of DC-modulation controller is converted to the non-linear optimization problem with parameter constraint,and then the constrained optimization problem has been converted to the unconstrained optimization problem.The gradient information of objective function is obtained by means of the simulation of trajectory sensitivity,and then the parameters of DC-modulation controller are optimized by Quasi-Newton Algorithm(DFP).Because the objective function reflects the power oscillation behavior of AC/DC interconnected power systems,the proposed method can be used to effectively damp the power oscillations of AC/DC system incurred by severe disturbances.The eigenvalue analysis and time domain simulations on the IEEE 4-generator AC/DC system verify the effectiveness and robustness of the proposed method.

DC modulation；trajectory sensitivity；Quasi-Newton algorithm；parameter optimization

TM712；TM743

A

1003-8930(2012)04-0030-06

2011-08-22；

2011-09-16

国家自然科学基金资助项目(50777046)；国家重点基础研究发展计划(973)资助项目(2009CB219700)