MMC-HVDC系统数学模型及其控制策略

曹春刚，赵成勇，陈晓芳

(华北电力大学(保定)电气与电子工程学院，保定 071003)

MMC-HVDC系统数学模型及其控制策略

曹春刚，赵成勇，陈晓芳

(华北电力大学(保定)电气与电子工程学院，保定 071003)

模块化多电平换流器MMC(modular multilevel converter)是电压源换流器型直流输电领域的一种新型拓扑,与传统的两电平存在一定的不同，因而对其建模及控制策略进行研究，有重要的意义。论文介绍了MMC的拓扑结构及工作原理。在考虑桥臂电抗的基础上，推导出模块化多电平换流器型直流输电MMC-HVDC(modular multilevel converter-high voltage direct current)的数学模型，进一步得到MMC-HVDC的简化电路图。在PSCAD/EMTDC下搭建了21电平MMC-HVDC系统，在dq同步旋转坐标系下，采用前馈解耦控制策略进行仿真研究，仿真结果验证了该数学模型的正确性和控制策略的有效性。

模块化多电平换流器；桥臂电抗；数学模型；简化电路图；控制策略

电压源换流器型直流输电VSC-HVDC(voltage source converter-high voltage direct current)，具有有功无功灵活可调、占地面积小、环境污染小、具备黑启动能力等显著优点，在可再生清洁能源(如风能和太阳能)的大力开发和利用，城市配电网转入地下改造等领域得到越来越广泛的应用[1～5]。

目前的VSC-HVDC工程大多采用两电平或三电平的VSC，开关器件的串联会导致器件的动态均压问题，影响系统运行的稳定性[6]。MMC通过子模块电压叠加达到较高的电压输出，输出电压谐波含量少。另外，模块化的结构使其可扩展性增强，为子模块的投入、退出运行提供了冗余，而且通过改变投入的子模块的数量，可实现电压及功率等级的灵活变化，并可扩展到更多的电平输出，因而MMC-HVDC更适合灵活的输电方式[7～10]。

MMC-HVDC作为应用于柔性直流输电领域的一种新兴技术，有其独特的优势，但国内外对于MMC-HVDC的研究时间还较短，实际工程的应用经验也较少，因而对于MMC-HVDC进行系统建模和控制策略方面的研究就有很重要的意义。文献[11]建立了MMC-HVDC系统的数学模型，并提出了适于MMC的控制策略，但建模过程中未考虑桥臂电抗的作用。文献[12]研究发现MMC每相上下两个交流输出端电位非常接近，进而认为是等电位的，通过等电位点虚拟短接，对MMC-HVDC进行了建模和控制策略的研究，其不足是对等电位点的认定是近似的。

本文分析了MMC拓扑结构和工作原理，在考虑桥臂电抗基础上，推导出MMC-HVDC系统的数学模型，并得到其等效的精确电路模型，根据该电路模型，把传统VSC的dq前馈解耦控制策略引入MMC-HVDC系统，最后在PSCAD/EMTDC环境下对数学模型和控制策略进行了仿真验证。

1 模块化多电平换流器的拓扑结构及工作原理

图1为MMC-HVDC一侧系统的拓扑结构。

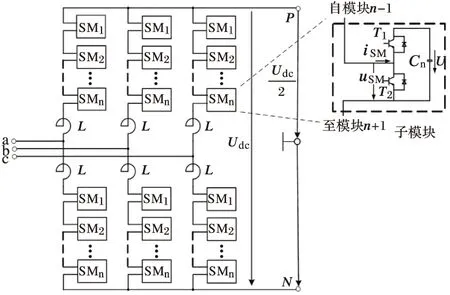
图1 MMC-HVDC一侧系统拓扑结构图

MMC每相由上下两个桥臂共2n个子模块SM(submodule)构成，每个桥臂由n个子模块和一个桥臂电抗L串联而成。其子模块由一个IGBT半桥和一个直流储能电容构成，uSM为子模块的端口输出电压，iSM为该子模块所在桥臂的电流，UC为子模块的电容电压。通过T1和T2的通断，可以使子模块处于投入、切除和闭锁三种状态，从而实现子模块的投入与切除。

对于模块化多电平换流器，每个桥臂的子模块可独立控制，从而每个桥臂可等效为一个可控的电压源。MMC一侧系统的等效电路图如图2所示。

图中，usa、usb、usc分别为交流系统三相母线电压的基波相量；isa、isb、isc分别为交流系统三相母线电流的基波相量；R、Lx分别为换流电抗器的等效电阻和等效电感；L为MMC换流器一相一个桥臂的桥臂电抗；ua、ub、uc分别为换流器三相输出电压的基波相量；uap、uad分别为a相上下桥臂的电压；ua1、ua2、ub1、ub2、uc1、uc2分别为三相上下桥臂除桥臂电抗器的电压。

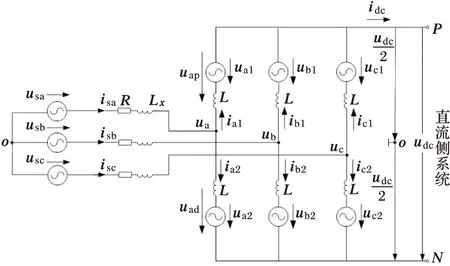
图2 模块化多电平换流器-侧系统等效电路图

以a相为例，由图2可得MMC系统的直流电压、交流电压和上下桥臂电压之间的关系为

(1)

(2)

由式(1)和式(2)可得

uap+uad=Udc

(3)

(4)

由式(3)和式(4)可得，MMC正常运行原理如下：

(1)直流电压是由换流器上桥臂和下桥臂的电压相加而得到的，为了保持直流电压的稳定，就必须保证每个相单元投入的子模块个数相等。

(2)通过调整上桥臂和下桥臂电压的幅值和相角，就可得到所期望的多电平电压输出。

2 考虑桥臂电抗的MMC-HVDC的数学模型与控制策略

2.1 考虑桥臂电抗的MMC-HVDC的数学模型

MMC与传统的两电平VSC的一个显著区别是：MMC系统每个桥臂由若干个结构相同的子模块与一个桥臂电抗器L串联构成。因而在系统建模时，桥臂电抗也应考虑在内。

考虑桥臂电抗时，MMC系统直流侧与交流侧电压、电流之间的关系如下

isa=ia1+ia2

(5)

(6)

(7)

(8)

由式(5)～式(8)可得

(9)

把式(9)代入式(7)整理可得

(10)

同理可得

(11)

(12)

式(10)～式(12)即为考虑换流电抗与桥臂电抗时，MMC-HVDC系统在三相静止坐标系下的数学模型，其进一步简化等效电路图如图3所示。

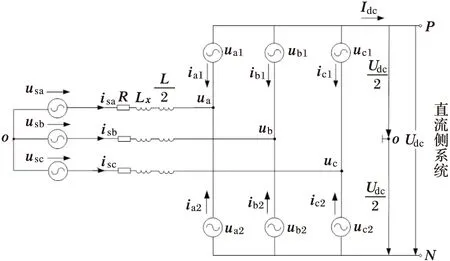
图3 MMC-HVDC一侧系统简化等效电路图

2.2 考虑桥臂电抗的MMC-HVDC的控制策略

由式(10)～式(13)和图3可知，等效后的MMC-HVDC系统，相当于上下桥臂电抗并联后再与换流电抗器串联，其结构与传统的VSC-HVDC类似，可采用传统的VSC-HVDC的控制策略[13～15]。

将式(10)～式(12)转换到dq坐标系可得

(13)

(14)

式中：usd、usq、id、iq分别为交流母线基波电压和交流母线基波电流的d轴和q轴分量；vd、vq分别为换流器输出基波电压的d轴和q轴分量。dq坐标系方向规定为：交流系统三相母线电压基波相量与d轴同相位，则usq=0。

(15)

式(13)和式(14)即为MMC-HVDC一侧系统在同步dq旋转坐标系下的数学模型。其内环电流控制器设计如下：

(16)

(17)

式中idref、iqref从外环功率控制器的输出获得。

在本文所选同步dq旋转坐标系下，稳态时交流系统与换流器交换的功率可表示为

(18)

(19)

式中us为交流母线三相电压基波相量的有效值。

由式(18)、式(19)可得，id、iq的估算值分别为

(20)

(21)

引入PI控制器，以消除稳态误差，结合式(20)和式(21)可得idref、iqref表达式为

(22)

(23)

当采用定直流电压控制时

idref=KP(udcref-udc)+KI∫(udcref-udc)dt

(24)

由式(16)、式(17)及式(22)～式(24)可得其控制原理图如图4所示。

图4 dq前馈解耦控制原理图

3 系统仿真与分析

为了验证推导出的MMC-HVDC系统的数学模型的正确性，在PSCAD/EMTDC中搭建了MMC-HVDC两端系统，采用上文推导出的控制策略，进行了仿真验证。

文献[16]对主电路参数进行了合理设计，交流系统参数为：两侧交流电源线电压有效值为220 kV，两侧换流变压器变比均为220/210 kV，换流电抗取0.1 p.u.，换流电感为5 mH，等效损耗电阻为1 Ω。直流侧系统参数为：额定直流电压Udc=400 kV。

换流器由6个桥臂构成，每个桥臂有20个子模块，电平数为21。子模块电容值为3 mF，桥臂电抗为40 mH。

MMC1侧采用定直流电压控制和定无功功率控制，MMC2侧采用定有功功率控制和定无功功率控制。

本文采用文献[17]的基于载波移相的电容电压平衡调制策略。

(1)无功功率阶跃情况下的仿真

直流电压不变，MMC1侧的无功功率定值在2.5 s时由0 Mvar阶跃到-40 Mvar，3 s时由-40 Mvar阶跃到40 Mvar。

MMC2侧的无功功率定值在2.5 s时由0 Mvar阶跃到-40 Mvar，3 s时由-40 Mvar阶跃到40 Mvar。仿真结果如图5所示。

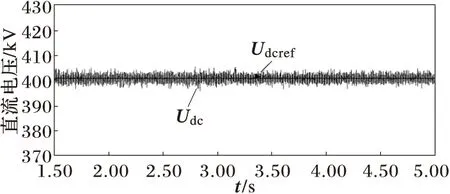
(a) MMC1侧直流电压

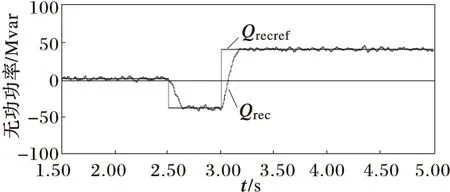
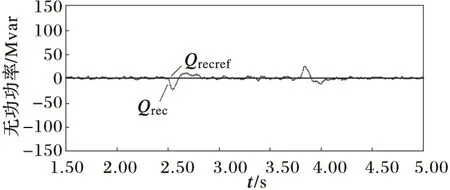
(b) MMC1侧无功功率

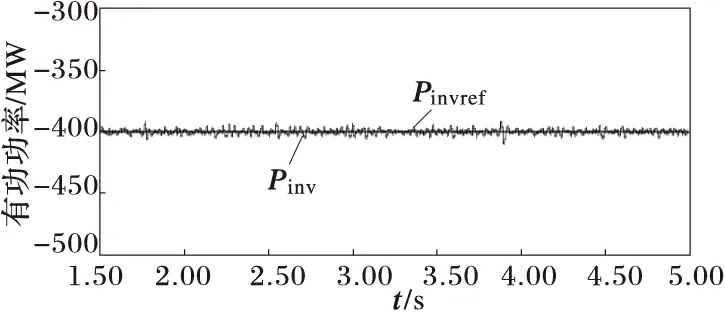
(c) MMC2侧有功功率

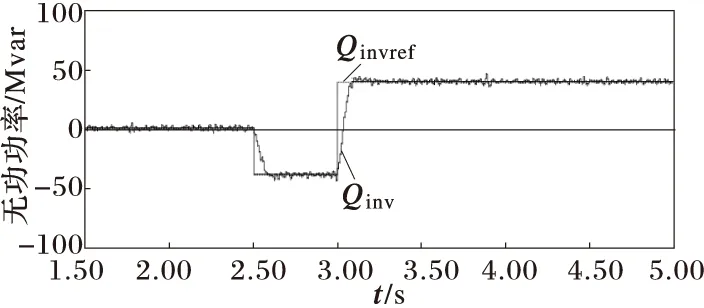
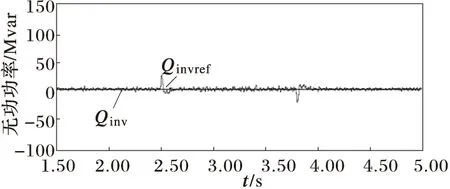
(d) MMC2侧无功功率

(2)有功功率阶跃情况下的仿真

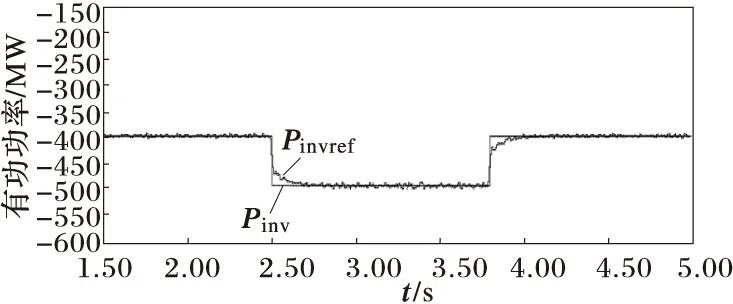
直流电压不变，无功功率定值为0 Mvar，MMC2侧有功功率定值在2.5 s时由-400 MW阶跃到-500 MW，3.8 s时由-500 MW阶跃到-400 MW。仿真结果如图6所示。

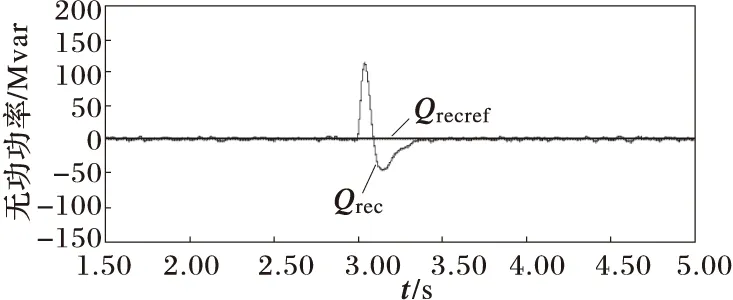
(3)有功功率翻转情况下的仿真

直流电压不变，无功功率定值为0Mvar，有功功率定值在3 s时由-400 MW变为100 MW，即3 s之前由MMC1侧向MMC2侧送400 MW的有功，3 s之后潮流翻转，由MMC2侧向MMC1侧送100 MW的有功。

仿真结果如图7所示。

从图(5)、图(6)和图(7)可以看出：

1)当无功功率、有功功率指令值发生阶跃时，系统的无功、有功能够快速跟踪指令值的变化，有功与无功之间的影响较小，解耦性能较好。

2)有功功率阶跃时，直流电压波动较小，且能较快的恢复稳定值。

3)当有功功率发生翻转时，对直流电压影响较大，但波动仍在10%以内，整流侧的无功功率有短时的波动，并较快恢复额定值，对逆变侧无功功率的影响较小。

由仿真分析可知，所搭建系统对于有功阶跃及无功阶跃都具有较快的响应速度，能较快的恢复稳定运行，并可快速地实现潮流翻转。

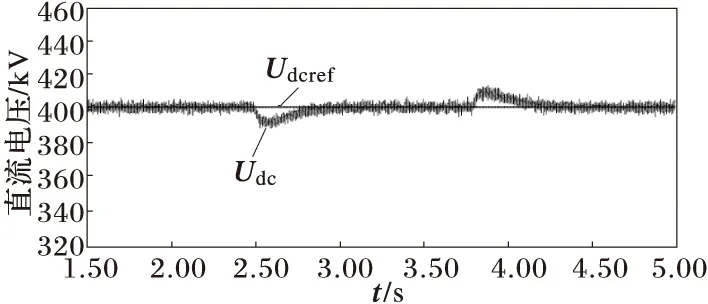
(a) MMC1侧直流电压

(b) MMC1侧无功功率

(c) MMC2侧有功功率

(d) MMC2侧无功功率

(a) MMC1侧直流电压

(b) MMC1侧无功功率

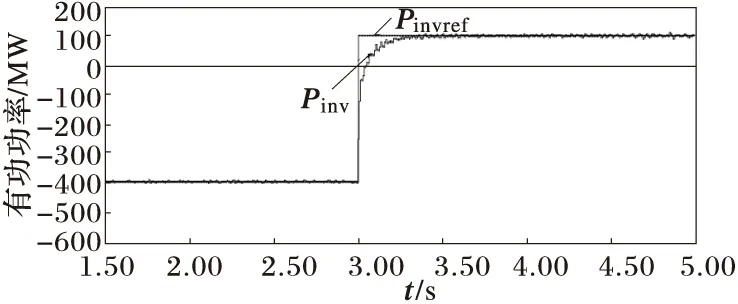
(c) MMC2侧有功功率

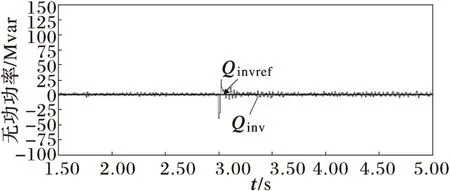
(d) MMC2侧无功功率

4 结语

本文在考虑桥臂电抗的基础上，推导出了MMC的数学模型，并得到其简化电路模型，该模型与传统VSC的拓扑结构类似。将传统VSC的控制策略应用到MMC系统中，通过对21电平MMC-HVDC系统进行建模仿真，验证了该数学模型的正确性以及dq前馈解耦控制策略的有效性。

[1]徐政，陈海荣(Xu Zheng，Chen Hairong)．电压源换流器型直流输电技术综述(Review and applications of VSC HVDC)[J]．高电压技术(High Voltage Engineering)，2007，33(1)：1-10．

[2]李庚银，吕鹏飞，李广凯，等(Li Gengyin，Lü Pengfei，Li Guangkai,etal)．轻型高压直流输电技术的发展与展望(Development and prospects for HVDC Light )[J]．电力系统自动化(Automation of Electric Power Systems)，2003，27(4)：77-81．

[3]Andersen B R，Xu L,Horton P J,etal．Topologies for VSC transmission[J]． Power Engineering Journal，2002，16(3)：142-150．

[4]Franquelo Leopoldo G，Rodriguez Jose，Leon Jose I，etal．The age of multilevel converters arrives[J]．IEEE Industrial Electronics Magazine，2008，2(2)：28-39．

[5]ABB．It is time to connect technical description of HVDC-light technology[R]．Ludvika，Sweden:ABB Power Technology，2005．

[6]Allebrod Silke，Hamerski Roman，Marquardt Rainer．New transformerless,scalable modular multilevel converters for HVDC-transmission[C]∥IEEE Annual Power Electronics Specialist Conference,Rhodes，Greece：2008．

[7]Lesnicar A，Marquardt R．A new modular voltage source inverter topology[C]∥European Power Electronics Conference,Toulouse ，France：2003．

[8]Dorn J，Huang H，Retzmann D．A new multilevel voltage-sourced converter topology for HVDC applications[C]∥International Council on Large Electric Systems,Paris，France：2008．

[9]屠卿瑞，徐政，郑翔，等(Tu Qingrui，Xu Zheng，Zheng Xiang，etal)．模块化多电平换流器型直流输电内部环流机理分析(Mechanism analysis on the circulating current in modular multilevel converter based HVDC )[J]．高电压技术(High Voltage Engineering)，2010，36(2)：547-552．

[10]管敏渊，徐政，屠卿瑞，等(Guan Minyuan，Xu Zheng，Tu Qingrui，etal)．模块化多电平换流器型直流输电的调制策略(Nearest level modulation for modular multilevel converters in HVDC transmission )[J]．电力系统自动化(Automation of Electric Power Systems)，2010，34(2)：48-52．

[11]刘钟淇，宋强，刘文华(Liu Zhongqi，Song Qiang，Liu Wenhua)．基于模块化多电平变流器的轻型直流输电系统(VSC-HVDC system based on modular multilevel converters )[J]．电力系统自动化(Automation of Electric Power Systems)，2010，34(2)：53-58．

[12]管敏渊，徐政(Guan Minyuan，Xu Zheng)．模块化多电平换流器型直流输电的建模与控制(Modeling and control for modular multilevel converters in HVDC transmission )[J]．电力系统自动化(Automation of Electric Power Systems)，2010，34(19)：64-68．

[13]尹明，李庚银，李广凯，等(Yin Ming，Li Gengyin，Li Guangkai,etal)．VSC-HVDC连续时间状态空间模型及其控制策略研究(Continuous-time state-space model of VSC-HVDC and its control strategy )[J]．中国电机工程学报(Proceedings of the CSEE)，2005，25(18)：34-39．

[14]陈蔓，陆继明，毛承雄，等(Chen Man，Lu Jiming，Mao Chengxiong,etal)．基于遗传算法的优化控制在VSC-HVDC中的应用(Application of genetic algorithm based optimal control in VSC-HVDC )[J]．电力系统及其自动化学报(Proceedings of the CSU-EPSA)，2006，18(4)：19-23．

[15]赵成勇，李金丰，李广凯(Zhao Chengyong，Li Jinfeng，Li Guangkai)．基于有功和无功独立调节的VSC-HVDC控制策略(VSC-HVDC control strategy based on respective adjustment of active and reactive power )[J]．电力系统自动化(Automation of Electric Power Systems)，2005，29(9)：20-24,30．

[16]殷自力，李庚银，李广凯，等(Yin Zili，Li Gengyin，Li Guangkai,etal)．柔性直流输电系统运行机理分析及主回路相关参数设计(Analysis on operational mechanism of VSC-HVDC and relevant parameter design of its main circuit )[J]．电网技术(Power System Technology)，2007，31(21)：16-21,26．

[17]Hagiwara M，Akagi H．PWM control and experiment of modular multilevel converters[C]//IEEE Power Electronics Specialist Conference,Rhodes，Greece：2008．

曹春刚(1986-)，男，硕士研究生，研究方向为高压直流输电与柔性输配电技术。Email:198672ccg@163.com

赵成勇(1964-)，男，博士生导师，教授，研究方向为高压直流输电与柔性输配电技术、电能质量分析与控制。Email:chengyongzhao@ncepu.edu.cn

陈晓芳(1987-)，女，硕士研究生，研究方向为高压直流输电与柔性输配电技术。Email:xiaofangrabbit@163.com

MathematicalModelandControlStrategyofMMC-HVDC

CAO Chun-gang，ZHAO Cheng-yong，CHEN Xiao-fang

(College of Electrical and Electronic Engineering，North China Electric Power University，Baoding 071003，China)

Modular multilevel converter(MMC)is a new topology in VSC-HVDC，which is different from the conventional two level VSC．Therefore，it is significant to study the modeling and control strategy of MMC-HVDC．The topology and working principle of MMC are introduced in this paper．Considering the reactance of the bridge，the mathematic model of the MMC-HVDC was developed，and the simplified circuit diagram of MMC-HVDC was obtained．The 21-level MMC-HVDC system was constructed in PSCAD/EMTDC environment．In the synchronousdqreference frame，the feed forward compensation control strategy is applied，and the simulation results verify that the mathematical model is correct and the control strategy is effective．

modular multilevel converter(MMC)；reactance of the bridge；mathematic model；simplified circuit diagram；control strategy

TM721.1

A

1003-8930(2012)04-0013-06

2011-08-22；

2011-09-08

“十一五”国家科技支撑计划重大项目(2010BAA01B01)；高等学校学科创新引智计划(B08013)