计及低碳效益的分布式发电优化配置

邓 晶，周任军，郑 思，任俞霖

（长沙理工大学，智能电网运行与控制湖南省重点实验室，长沙410114）

分布式电源（包括储能）大量接入电网，是顺应环境保护、节能减排和可持续性发展的重要趋势。研究表明DG不同的安装位置和容量，将会影响到系统短路电流的大小、配电网的电压分布、系统网损、继电保护等［1～3］。

分布式电源选址和定容的问题属于多变量优化问题，国内外学者从不同角度对DG优化配置问题进行了研究，取得了丰富的成果。文献［4］建立了链式配电网络、恒功率静态负荷模型和分布式电源的功率模型，提出一种图解与遗传算法相结合的计算方法。文献［5］研究了多负荷水平下计及节能调度的配电网分布式电源（DG）优化配置问题，建立了2层规划数学模型，使DG并网运行价值最大化。文献［6］对分布式发电的可行接入位置以及注入容量限制进行了理论探讨。文献［7］通过计算微增率确定分布式发电的安装位置，在确定容量时，充分考虑环境因素，使得结果有利于环境保护。文献［8］采用Tabu搜索算法求解分布式优化配置问题。文献［9］以最大化有功输出为目标函数，将线路的热稳定极限加入约束中，利用线性规划求解规划模型。文献［10］提出的规划模型以供电公司的总成本最小为优化目标。

但是国内外文献中将低碳效益和分布式发电优化配置相结合的研究尚不多见。通常人们认为，开展分布式发电优化配置研究的主要目标是降低网损，提高经济效益，减少SO2等污染气体的排放，对低碳效益却缺乏足够重视，而现实情况是：作为CO2排放的主体，有效控制并减少碳排放成为电力行业所面临的突出问题，而电源规划则将在其中发挥着至关重要的作用。所以将低碳效益纳入优化配置模型中具有实际意义。

基于以上原因，本文针对电力系统各个环节进行低碳分析，推导出发电侧低碳费用的计算公式，首次将低碳效益作为评估配电网效益的重要指标加入分布式发电多目标优化配置模型，改变了传统的分布式发电优化配置模式，使分布式发电的节能减排优势最大化。

1 电力系统低碳分析

在整个电力系统中，低碳概念不仅在其能源侧、发电侧，而是在输配电侧、用户侧等各个环节均有影响。针对每个环节，分析和总结出各自实现低碳电力的关键技术和措施，如表1所示。

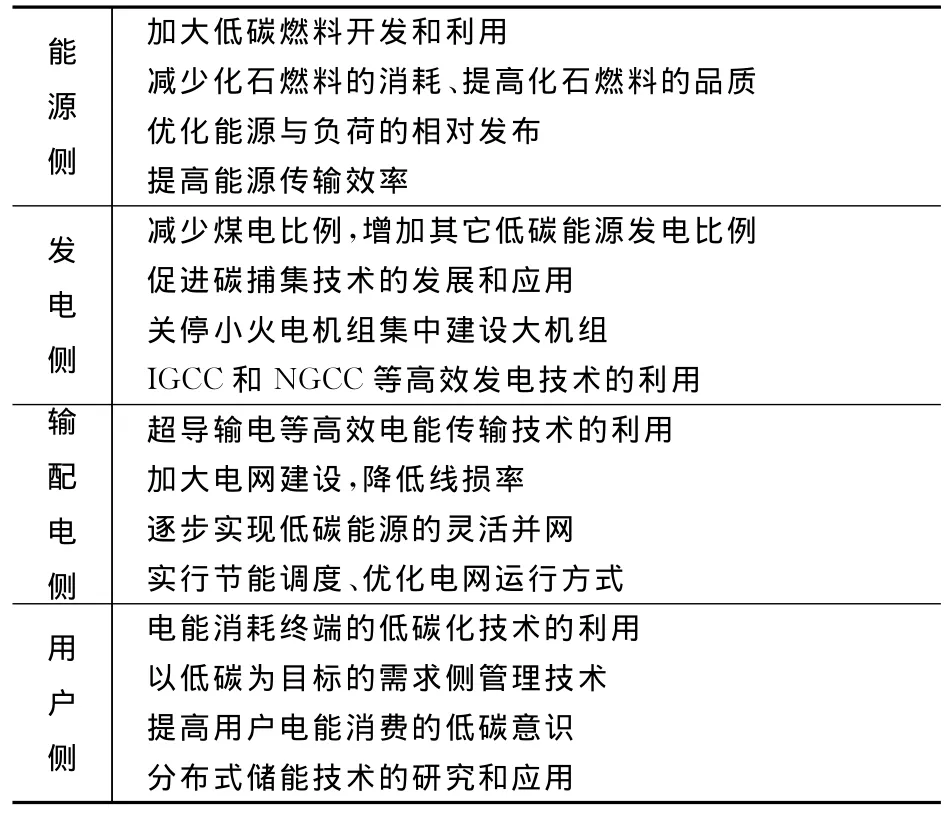
表1 电力系统低碳环节分析及技术措施Tab.1 Power system low－carbon analysis and technical measures

发电侧作为电力生产链的源头，在实现低碳电力中扮演非常重要的角色，中国电力生产主要所利用的一次能源以煤炭为主，生产单位电能的CO2排放强度约为0.82kg／（kW·h）［11］，所以现阶段实现发电侧低碳化显得更加紧迫，而风电、光伏等近零碳排放发电的并网正是实现发电侧低碳化的最佳途径。

2 分布式发电优化配置指标

2.1 低碳费用指标

相对于传统火力发电机，DG排放很少量的CO2，所以DG的接入能够有效降低低碳费用，提高低碳效益。

1）低碳费用成本

低碳费用成本由低碳投入成本和低碳损失成本两部分组成，即

其中：cc为低碳费用成本；cd为低碳投入成本；cf为低碳损失成本。

低碳投入成本cd是指发电商为减轻碳污染，从事节能减排活动而支付的费用，这部分成本可根据设备技术初投资、相关运行活动费用估算得出。

低碳损失成本cf指的是发电机因排放二氧化碳而支付的费用成本，即发电商向政府部门交纳的碳排放费或者罚款的费用成本，这部分成本是根据国家制定的碳排放收费标准和二氧化碳的排放量计算得出：

式中：Eco2为发电机单位有功出力产生的CO2的排放量；λco2为CO2排放惩罚价格。

2）低碳费用指标

低碳费用指标ΔE可表示为

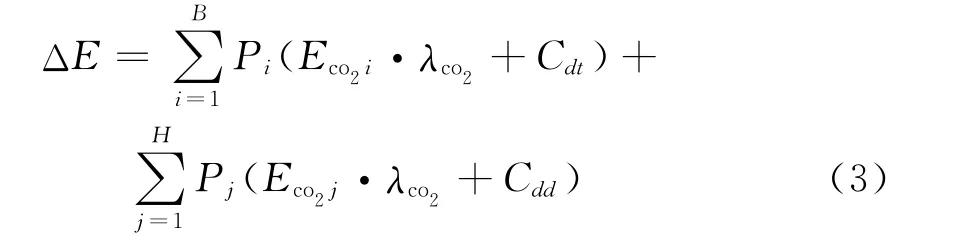
式中：B、H分别为系统中传统发电机台数和DG台数；Pi、Pj分别为传统发电机和DG的有功出力；Eco2i、Eco2j分别为传统发电机和DG单位有功出力产生的CO2排放量；λco2为CO2排放惩罚价格；Cdt、Cdd分别为传统发电机和DG的低碳投入成本。

2.2 电压安全指标

在分布式电源接入配电网之后，配电系统从放射状无源网络变为有源网络，潮流的大小和方向都将发生巨大改变，从而使配电网中某些位置的电压也发生变化。电压安全指标的建立能够评估DG的位置和注入功率对配电网全局电压的影响，而用户要求节点电压在保证合格的基础上尽量减少与标准值1.0（标幺值）的偏差，所以定义电压安全指标为各节点的电压偏移总和［12］：

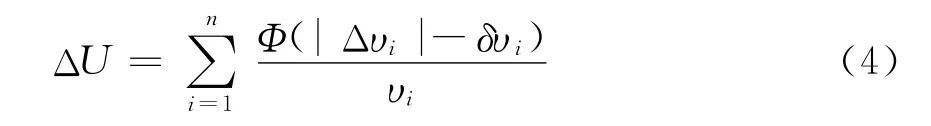
式中：n为配电网的节点数；υi为节点i的电压；Δυi为节点i的电压偏差量。标幺化以后，Δυi＝1－υ；δυI为节点i可忽略的最大电压偏差量；设x＝｜Δυ｜－δυi，则函数Φ（x）可以表示为

本文取δυi为－1% ～＋1%，当电压偏差在这个范围内时认为电压偏差忽略不计。

2.3 有功网损指标

分布式电源接入配电网改变了系统潮流分布，一般会减小支路潮流流动，从而有利于减小网损，但是当DG注入功率过高时，支路潮流流动反而可能增大，所以网络损耗不仅与负荷大小有关，同时还与分布式电源的安装位置以及分配到各节点的功率值有关。采用配电网支路的有功网损的总和作为指标：

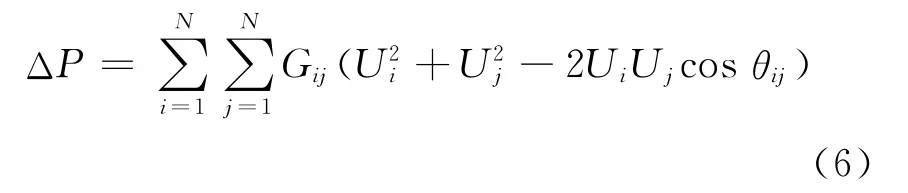
式中：N为系统节点数；Gij为线路ij的电导；Ui／Uj分别为节点i和j的节点电压；θij为节点i与节点j之间的相角差。

3 分布式发电配置多目标优化模型

3.1 目标函数

由上可知，分布式电源接入配电网后，对低碳费用、电压安全、有功网损都会带来影响，以此三项指标作为分布式电源优化配置问题的多目标，其目标函数：

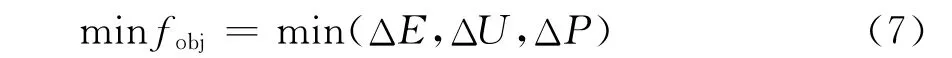
其中，ΔE，ΔU，ΔP分别如式（3）、（4）、（6）描述。

3.2 约束条件

等式约束为潮流方程：

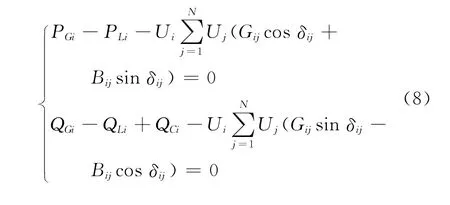
不等式约束为

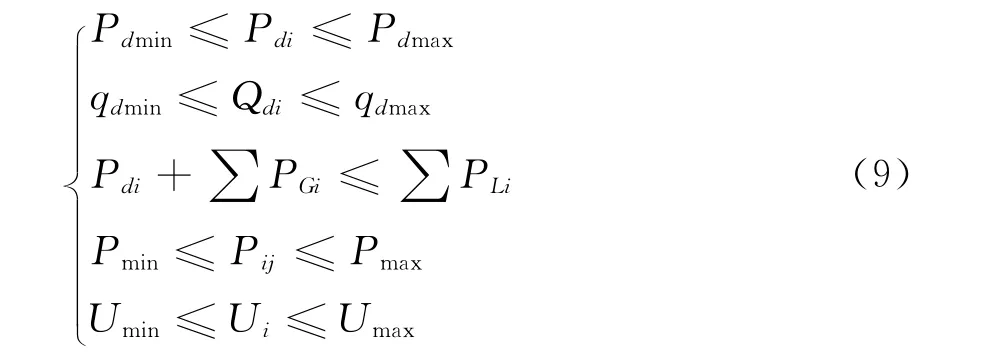
式中：PGi、QGi分别为发电机有功、无功出力；PLi、QLi分别为发电机有功、无功负荷；QCi为无功补偿容量；Ui为节点电压大小；Gij、Bij为系统导纳；δij为节点电压相角差；Pdi、Qdi分别为DG的有功、无功出力；j∈i表示与节点 相连的节点；变量添加下标min、max分别表示该变量的下限和上限。

3.3 优化模型转换

由于3个优化子目标具有不同的量纲，为协调不同目标之间的关系，本文在多目标优化模型中引入满意度值μ。μ是与各个目标函数值相关的复合函数，也称为隶属度函数。它反映了多目标优化结果与各个单目标优化结果之间的“距离”。满意度值越大，相应的解与单目标优化解越接近。于是原来的多目标优化问题就转化成以隶属度函数值最大为目标的单目标优化问题，引入降半直线型函数来表示各子目标的模糊隶属度函数：

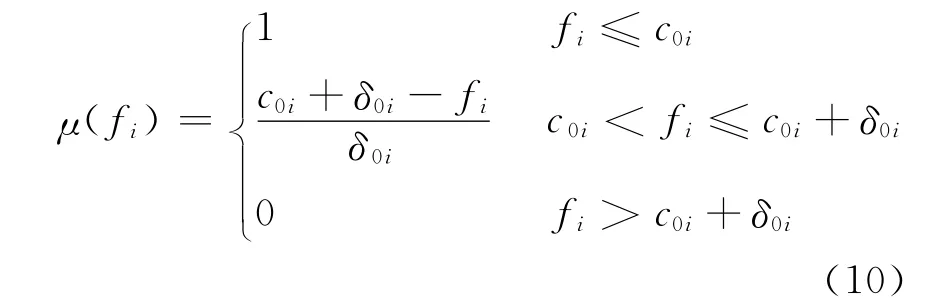
式中：i＝1，2，3；μ（fi）对应低碳效益、电压安全和有功网损3个优化子目标的隶属度；c0i为对3个子目标单独优化得到的最佳目标值；c0i＋δ0i表示目标函数优化中最高可接受的上限值。

经过上述模糊化处理，原多目标规划问题就转化为单目标规划问题：

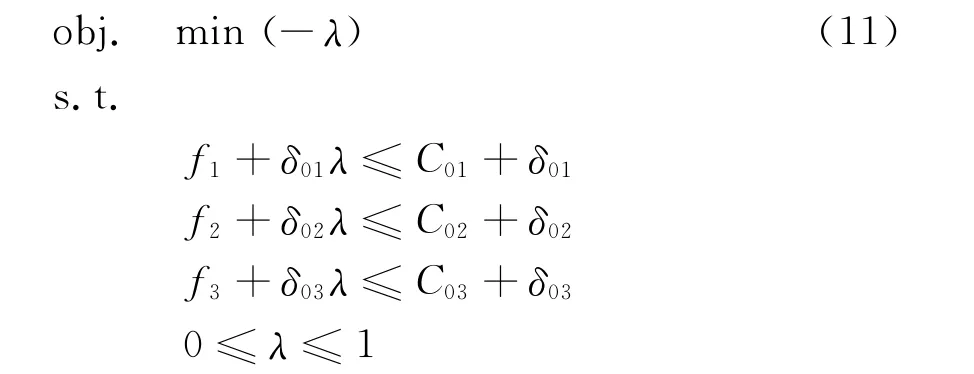
式 中：λ为 总 体 满 意 度，λ＝ min｛μ（f1），μ（f2），μ（f3）｝。

约束还有式（8）、式（9）。

4 模拟植物生长算法求解DG规划

模拟植物生长算法是将优化问题的可行域作为植物的生长环境，将全局最优解当作光源，模拟真实植物生长的向光性机理，建立枝叶在不同光线强度环境下向光源快速生长的动力机制［13］。文献［14］采用以植物向光性理论为基础的概率生长模型对这一过程进行了模拟。假设树干的长度为M，树从树根所在的点S0开始生长，在经历若干次生长后，上面有k个比树根好的初始生长点SMk，所对应的形态素浓度为PMk，按下式计算树上各生长点的形态素浓度值：

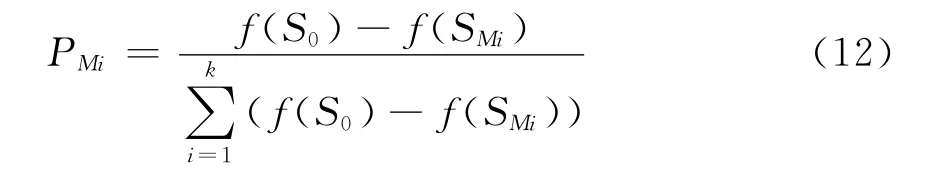
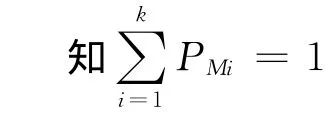
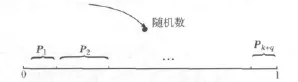
图1 形态素浓度构成的状态空间Fig.1 Morphactin concentration state space

利用PGSA求解DG优化配置的流程如图2所示。

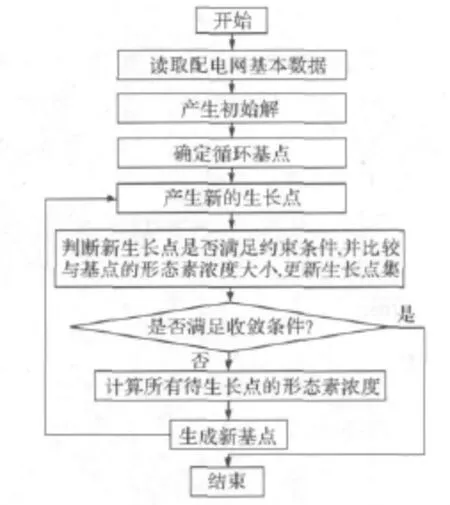
图2 PGSA求解DG规划流程Fig.2 Flow chart of planning of DG based on PGSA

DG优化配置涉及到DG待选节点和安装容量两个决策变量。待选节点可以描述成整数序列形式，｛m1、m2、m3、…，mNDG｝，则节点mi处 DG 的安装容量为mipr，当mi为0时表示该节点不安装DG。规划程序首先单独以式（3）、式（4）和式（6）这3个优化子目标为适应度函数，分别求出c01、c02和c03；然后再以式（11）为目标进行优化，求出总体满意度最好的DG规划方案。

5 算例分析

以IEEE30节点系统为例，根据本文提出的方法计算分布式电源最佳位置和最佳容量。

IEEE30节点系统中包括6台发电机（1、2、5、8、11、13号节点上接有常规机组，节点1为平衡节点）、4台变压器、4个无功补偿装置，有功负荷为162MW，无功负荷为94Mvar。算例中所采用的DG的额定容量为100kW，各待选节点允许安装的最大容量为1MW，DG规划总容量不超过1MW。假设只在三个节点接入分布式电源，选取节点7、9、10、14、15、17、22、23、24、29、30 作 为 并 网 备选点。

表2是本文根据传统发电厂的机组特性和相关环境政策设定的IEEE 30节点系统发电机低碳费用的计算参数，并假设DG释放的二氧化碳量很少，可以忽略不计。

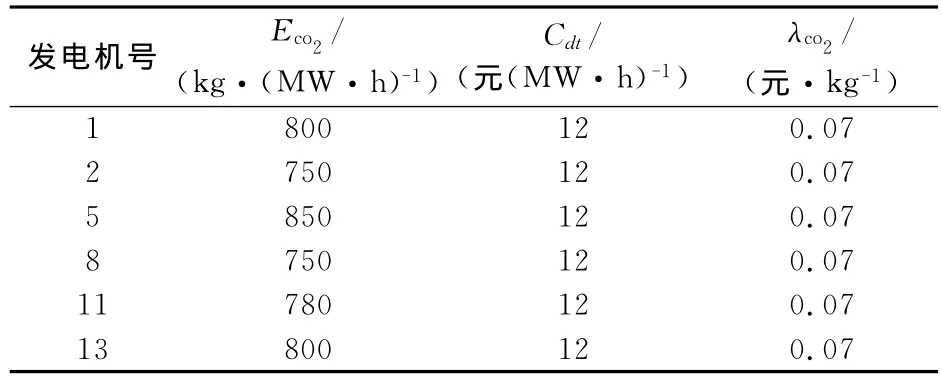
表2 系统发电机低碳费用的计算参数Tab.2 Calculation parameters of low－carbon expense in generator

分别计算出在未安装DG时和安装DG后系统的低碳费用、电压安全和系统网损，计算结果如表3所示。

表3 系统优化结果Tab.3 System optimization result

求解得出DG的最优配置为：节点30安装5台，节点9安装3台，节点15安装2台；3个优化指标的值分别为 ΔE＝64元、ΔU＝0.0104、ΔP＝3.7560MW。算例计算结果（见表3）表明，安装DG后系统的低碳费用、比安装DG前都有所降低，节点电压安全指标由0.0127下降到0.0104，有功网损由4.9562MW 降低到3.7560MW。由此可见，采用本文方法确定DG的地址和出力，可有效减少碳排放，改善系统的运行条件，提高系统电压的运行水平，减少有功网损。

表4是针对各个单目标进行规划的结果，其中方案1、方案2和方案3分别对应低碳效益、电压安全和有功网损三个子目标的DG优化配置，求得的f1，f2和f3分别为62元／（MW·h），0.0000和3.204MW。从表3可知：方案1只强调了低碳费用的减少，而在降低网损和改善系统电压安全性方面有所欠缺；方案2强调改善系统电压安全性，但是同样在低碳费用上付出了更高的代价；方案3强调了网损的优化，但是在其他两方面都受到相应的损失。

表4 单目标优化结果Tab.4 Single objective optimization result

比较表3和表4数据可知：相对于单目标优化模型，多目标优化模型确定的DG配置能在各目标之间进行协调权衡，使所有目标函数尽可能达到最优，综合效益更高，更能满足实际需求。

表5比较了PGSA和遗传算法GA（genetic algorithm）对算例的仿真情况。两种算法得到的优化结果完全一致，计算时间略有不同。与遗传算法相比，PGSA不需要设置惩罚系数、交叉率、变异率等影响算法计算速度和收敛性的参数，算法的稳定性高，计算时间短。

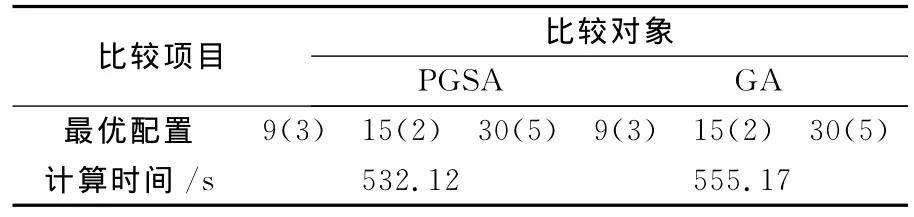
表5 植物生长模拟算法与遗传算法的比较Tab.5 Comparison of PGSA and GA

6 结语

在分析和总结低碳电力发展的基础上，提出发电侧低碳费用的计算公式，以低碳费用、电压安全、有功网损三个指标评估含分布式发电的配电网效益，建立分布式发电配置的多目标优化模型，采用最大满意度法转化多目标优化问题为单目标，并用模拟植物生长算法对上述模型进行求解。算例分析表明：将低碳效益纳入优化模型中，能够更加全面地评估分布式发电的优势，改变了传统分布式发电优化配置中只考虑经济效益的单一模式，有效减少二氧化碳的排放，提高系统电压的运行水平，降低系统有功网损。

［1］ 王守相，王慧，蔡声霞（Wang Shouxiang，Wang Hui，Cai Shengxia）.分布式发电优化配置研究综述（A review of optimization allocation of distributed generations embedded in power grid）［J］.电力系统自动化（Automation of Electric Power Systems），2009，33（18）：110－115.

［2］ 张勇（Zhang Yong）.分布式发电对电网继电保护的影响综述（Review of impact of distributed generation on distribution system protection）［J］.电力系统及其自动化学报（Proceedings of the CSU－EPSA），2010，22（2）：145－151.

［3］ Naveen Jain，Singh S N，文福拴（Wen Fushuan）.分布式发电当前趋势与将来挑战（Distributed generation recent trends and future challenges）［J］.电力科学与技术学报（Journal of Electric Power Science and Technology），2008，23（4）：53－61.

［4］ 李鹏，廉超，李波涛（Li Peng，Lian Chao，Li Botao）.分布式电源并网优化配置的图解方法（A graph－based optimal solution for siting and sizing of grid－connected distributed generation）［J］.中国电机工程学报（Proceedings of the CSEE），2009，29（4）：91－96.

［5］ 唐勇俊，刘东，阮前途，等（Tang Yongjun，Liu Dong，Ruan Qiantu，etal）.计及节能调度的分布式电源优化配置及其并行计算（Optimal allocation of distributed generation and its parallel computation considering energy－saving dispatching）［J］.电力系统自动化（Automation of Electric Power Systems），2008，32（7）：92－97.

［6］ 王志群，朱 守真，周双 喜，等 （Wang Zhiqun，Zhu Shouzhen，Zhou Shuangxi，etal）.分布式发电接入位置和注入容量限制的研究（Study on location and penetration of distributed generations）［J］.电力系统及其自动化学报（Proceedings of the CSU－EPSA），2005，17（1）：53－58.

［7］ 郑漳华，艾芊，顾承红，等 （Zheng Zhanghua，Ai Qian，Gu Chenghong，et al）.考虑环境因素的分布式发电多目标优化配置（Multi－objective allocation of distributed generation considering environmental factor）［J］.中国电机工程学报（Proceedings of the CSEE），2009，29（13）：23－28.

［8］ Gandomkar M，Vakilian M，Ehsan M.A genetic based Tabu search algorithm for optimal DG allocation in distribution networks ［J］.Electric Power Components and Systems，2005，33（12）：1351－1362.

［9］ Keane A，O＇Malley M.Optimal allocation of embedded generation on distribution networks［J］.IEEE Trans on Power Systems，2005，20（3）：1640－1646.

［10］ El－Khattam W，Bhattacharya K，Hegazy Y，et al.Optimal investment planning for distributed generation in a competitive electricity market［J］.IEEE Trans on Power Systems，2004，19（3）：1674－1684.

［11］ 陈 启 鑫，康 重 庆，夏 清，等 （Chen Qixin，Kang Chongqing，Xia Qing，et al）.电力行业低碳化的关键要素分析及其对电源规划的影响（Key low－carbon factors in the evolution of power decarbonisation and their impacts on generation expansion planning）［J］.电力系统自动化（Automation of Electric Power Systems），2009，33（15）：18－23.

［12］ 王新刚，艾芊，徐伟华，等（Wang Xingang，Ai Qian，Xu Weihua，et al）.含分布式发电的微电网能量管理多目标优化（Multi－objective optimal energy management of microgrid with distributed generation）［J］.电力系统保护与控制（Power System Protection and Control），2009，37（20）：79－83.

［13］ 李彤，王春峰，王文波，等（Li Tong，Wang Chunfeng，Wang Wenbo，et al）.求解整数规划的一种仿生类全局优化算法——模拟植物生长算法（A global optimization bionics algorithm for solving integer programming－Plant growth simulation algorithm ）［J］.系统工程理论与实践（Systems Engineering－Theory＆ Practice），2005，25（1）：76－85.

［14］ 杨丽徙，王锴，程杰（Yang Lixi，Wang Kai，Cheng Jie）.应用改进模拟植物生长算法求解无功优化问题（Application of modified plant growth simulation algorithm in solution of reactive power optimization problem ）［J］.高电压技术（High Voltage Engineering），2009，35（3）：694－698.