直流输电对电力系统动态稳定性影响分析
陈厚合,姜 涛,李国庆
(1.东北电力大学电气工程学院,吉林132011;2.天津大学智能电网教育部重点实验室,天津300072)
交直流系统中,直流功率调制作为改善系统动态稳定性的辅助手段在电力系统发挥着巨大作用[1]。直流功率调制是指在直流控制系统中加入附加功率调制环节,从直流系统两端的交流系统或并联交流联络线上提取反映系统异常的信号以调节直流输电系统传输的有功功率,充分发挥直流系统的快速可控性,快速补偿或吸收其所联交流系统的功率缺额或过剩,改善交流系统动态稳定性[1~4]。
交直流系统动态稳定性与直流功率调制有关,与直流系统的控制策略也相关[5~7]。文献[8]采用概率特征根分析法研究了直流控制方式及参数对系统动态稳定性的影响,研究结果表明,整流侧定电流控制有利于系统的小扰动稳定;文献[9]针对南方电网多回直流的研究表明,计及交流换相电压的影响,整流侧定电流控制比定功率控制更有利于南方电网的暂态稳定性;文献[10]指出,在控制系统各环节参数选择恰当的条件下,采用定电流控制与定功率控制对电网的稳定影响程度相当。现研究表明,在交直流混合系统中整流侧定电流控制有利于系统的动态稳定,但均未结合直流调制环节综合考虑,且所研究的直流系统模型也不尽相同。
本文在PSS/E下搭建含标准直流模型的典型交直流混合系统;建立交直流混合系统网络方程,并将其线性化处理以推导系统动态方程;针对直流输电系统的动态特性与直流控制策略密切相关的特点,以整流侧定电流-逆变侧定熄弧角为例,构建多机交直流系统动态模型,并采用根轨迹法设计直流功率调制环节;借助模态分析法和时域仿真,充分考虑直流系统控制方式、直流功率调制策略研究直流输电系统对系统动态稳定性的影响。
1 直流系统数学模型
直流输电系统换流器数学模型为
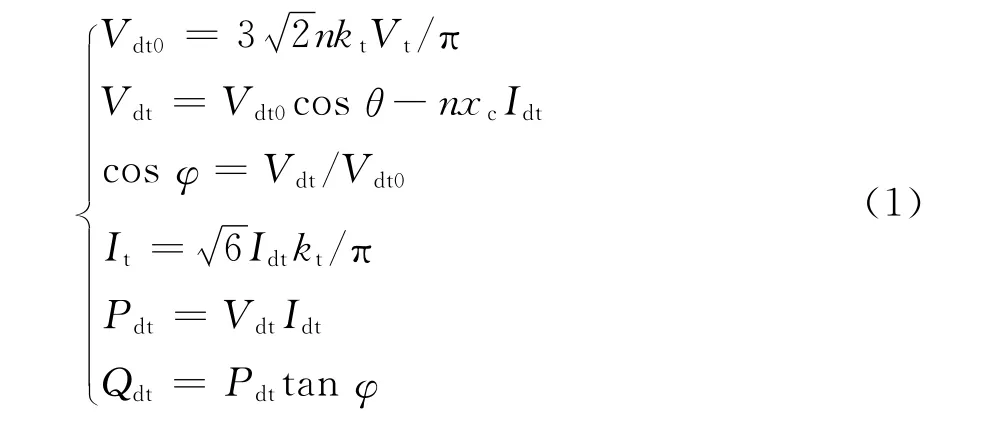
直流传输动态方程为
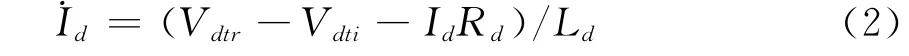
式中:Vt为换流变压器高压母线电压有效值;kt为换流变压器变比;n为换流器桥数;φ为功率因数角;Pdt和Qdt分别为换流站吸收的有功和无功功率;Xc为单桥换流电抗;Vdt为换流器节点直流侧电压;Vdt0为换流器节点直流侧空载电压;Idt为换流器节点直流侧电流,流出节点为正;cosθ为整流器触发角α或逆变器熄弧角γ的余弦值;It为流入换流变压器的交流电流。
直流控制系统如图1所示[11],由图1可知直流
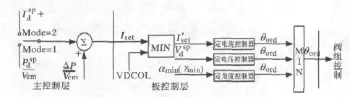
图1 直流输电系统控制系统示意图Fig.1 Control system of DC power system
常用控制方式为:定功率控制(CP)、定电流控制(CC)、定电压控制(CV)和定角度控制(CA),计及直流调节动态过程,各种控制方式下的动态方程为
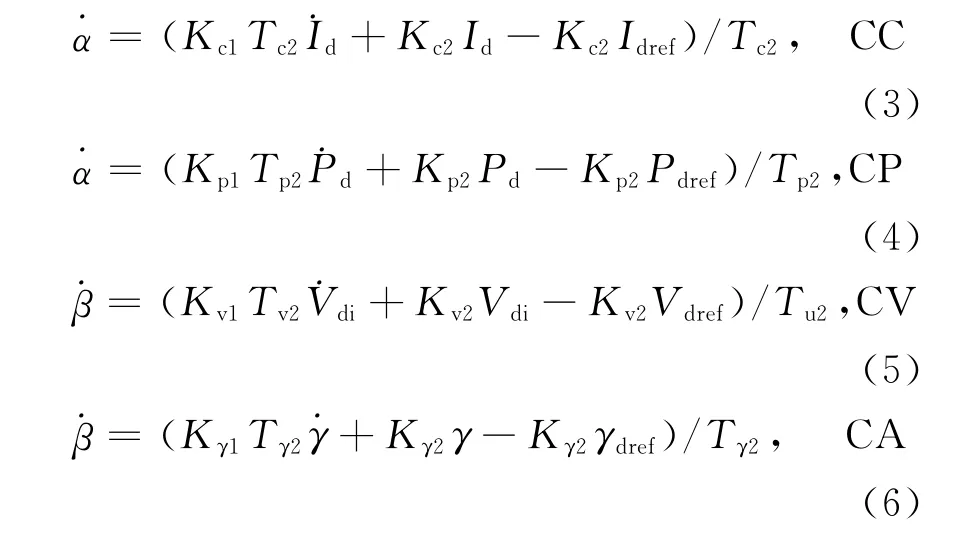
式中:α、β分别为直流整流侧、逆变侧触发角;γ为直流逆变侧熄弧角;Id为直流线路上流过的电流;Pd为直流系统传输的有功功率;Vdi为逆变侧直流电压;Idref、Pdref、Vdref及γdref分别表示定电流控制、定功率控制、定电压控制及定熄弧角控制预设值;Tc1和Tc2为定电流控制的调节时间常数;Tp1和Tp2为定功率控制的调节时间常数;Tv1和Tv2为定电压控制的调节时间常数;Tγ1和Tγ2为定熄弧角控制的调节时间常数;Kc1和Kc2为定电流控制的调节增益;Kp1和Kp2为定功率控制的调节增益;Kv1和Kv2为定电压控制的调节增益;Kγ1和Kγ2为定熄弧角控制的调节增益;Kc、Kp、Kv、Kγ分别表示定电流控制、定功率控制、定电压控制及定熄弧角控制环节的增益。
直流输电系统在传输电能的同时,利用直流调制可充分发挥直流系统的快速可控性,改善交流系统运行性能[12]。直流调制原理框图如图2所示,由图2可知直流调制环节的传递函数为
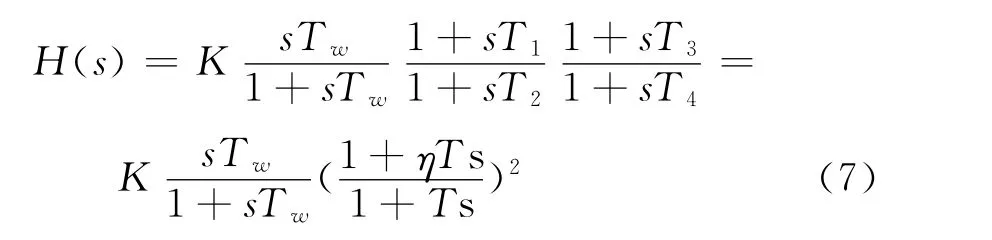
式中:K为调制增益;Tw为功率调制隔直环节时间常数;T1、T2、T3、T4及Ts为时间常数;η为系数。
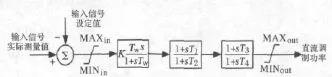
图2 直流调制框图Fig.2 Block diagram of HVDC modulation
2 交直流网络模型
采用导纳矩阵表示的交直流系统网络方程为

式(8)在直角坐标系下的节点注入电流微增量与节点电压微增量之间满足如下关系:
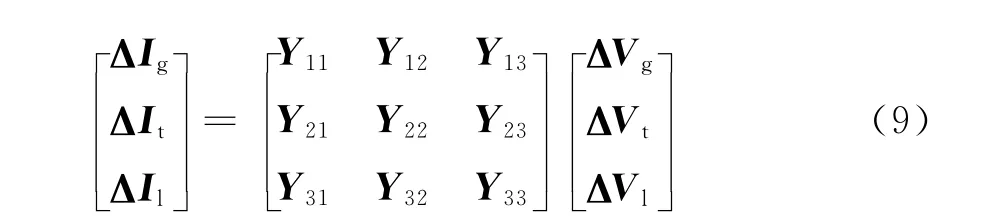
式中:ΔIg、ΔVg为发电机节点机端电流相量微增量集合、电压相量微增量集合;ΔIt、ΔVt为直流换流母线的电流相量微增量集合、电压相量微增量集合;ΔIl、ΔVl为负荷节点母线的电流相量微增量集合、电 压 相 量 微 增 量 集 合;Y11、Y12、Y13、Y21、Y22、Y23、Y31、Y32、Y33分别为节点导纳矩阵的子矩阵。
负荷节点的电流、电压微增量之间可表示为
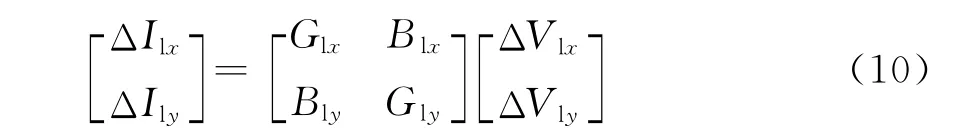
式中,
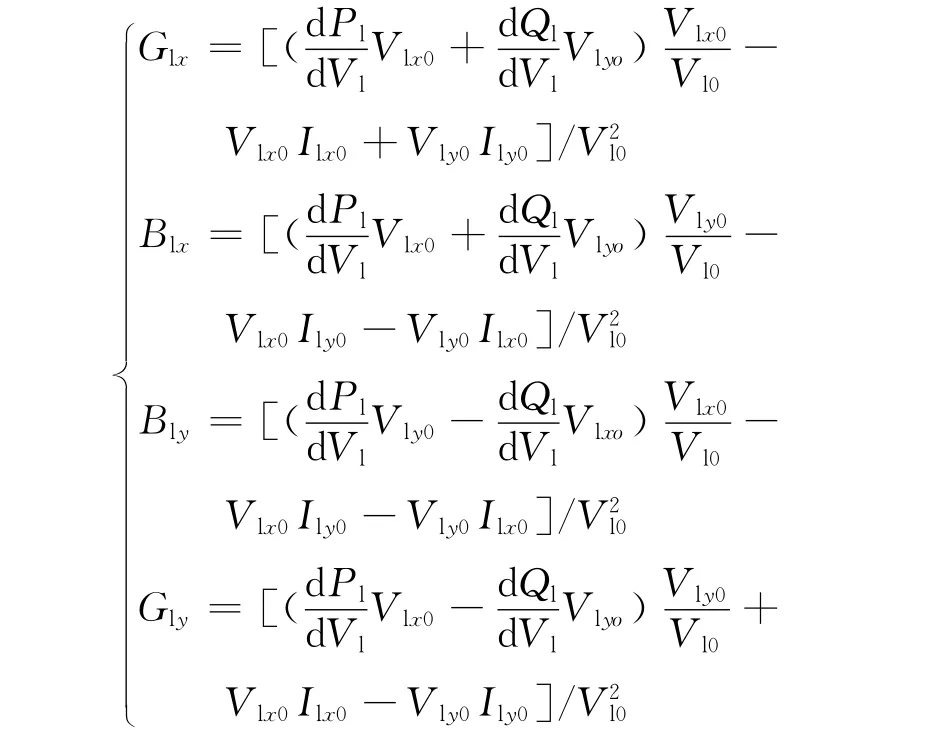
ΔIlx、ΔIly为负荷节点电流的x轴分量、y轴分量的微增量;ΔVlx、ΔVly为负荷节点电压的x轴分量、y轴分量的微增量;Vl为负荷节点电压幅值;Pl、Ql为负荷节点有功功率、无功功率;Vl、Vlx0、Vly0为负荷节点电压的幅值、x轴分量、y轴分量的初始值;Ilx0、Ily0为负荷节点电流的x轴分量、y轴分量的初始值。
将式(10)代入式(9)中,消去全部负荷节点注入电流微增量,仅保留发电机节点、换流站节点的线性化方程为
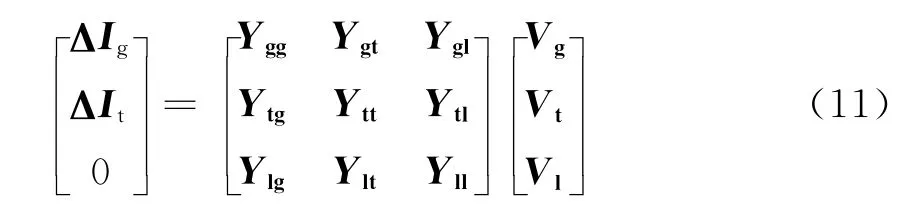
3 交直流系统动态模型
线性化的发电机状态方程为[13]:
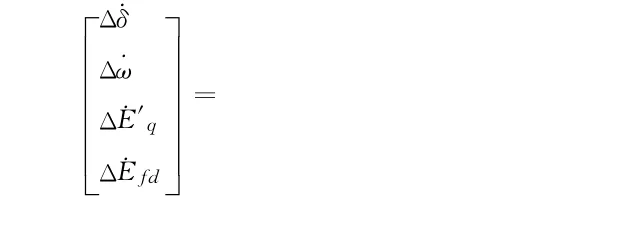
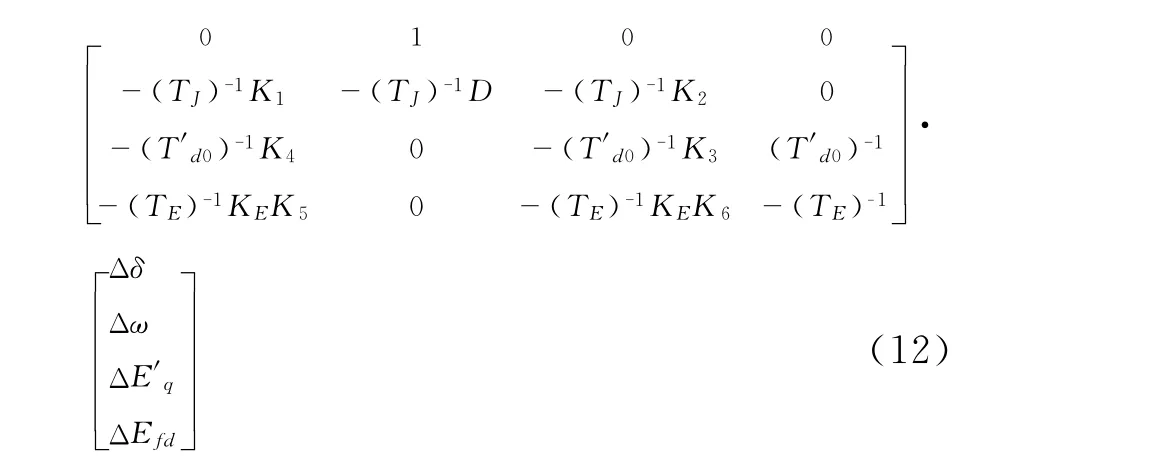
式中,
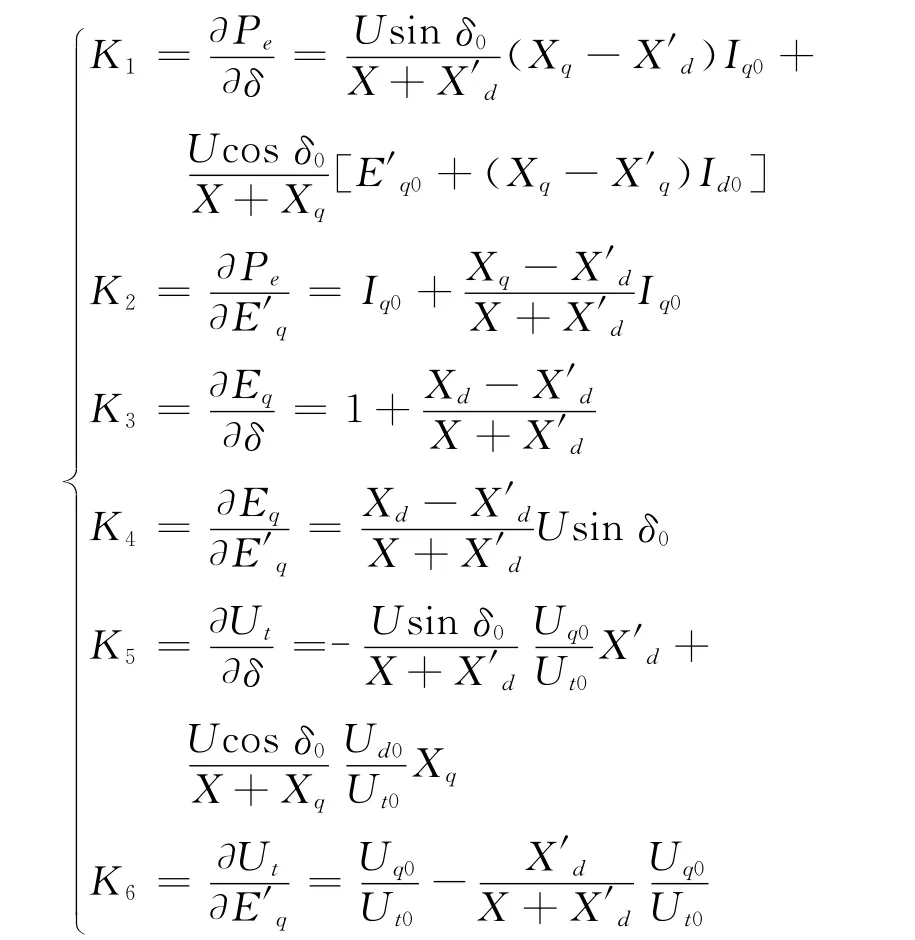
式中:δ为发电机转子角;ω为发电机转速;Eq为发电机空载电势;E′q为发电机暂态电势;Efd为发电机励磁电势;TJ为发电机惯性常数;D为发电机阻尼系数;T′d0为发电机d轴定子绕组开路下的励磁绕组暂态时间常数;TE为d轴开路暂态时间常数;KE为励磁放大增益;U为无穷大系统电压;Ut为发电机端电压;Pe为发电机输出的电磁功率;X为发电机与无穷大系统间电抗;Xq为发电机q轴同步电抗;Xd为发电机d轴同步电抗;X′d为发电机d轴暂态电抗;δ0为发电机转子角初始值;Iq0为发电机q轴电流分量;Id0为发电机d轴电流分量;Ud0、Uq0、Ut0分别为发电机d轴、q轴及机端电压幅值。
将d、q坐标下发电机电压、电流分别变换到直角坐标系下,对应的机端电流微增量形式为
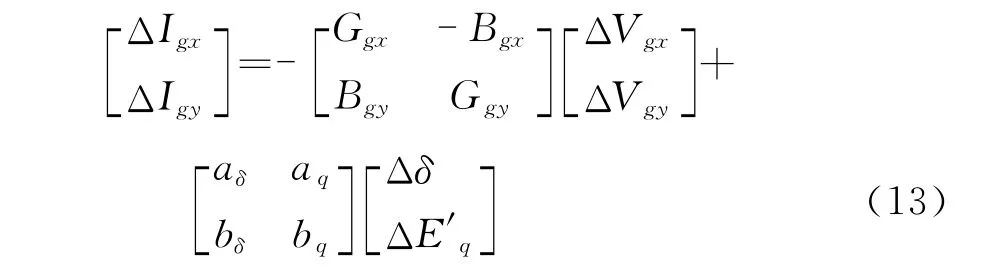
其中
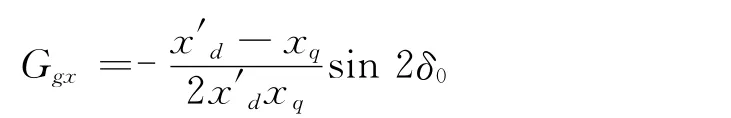
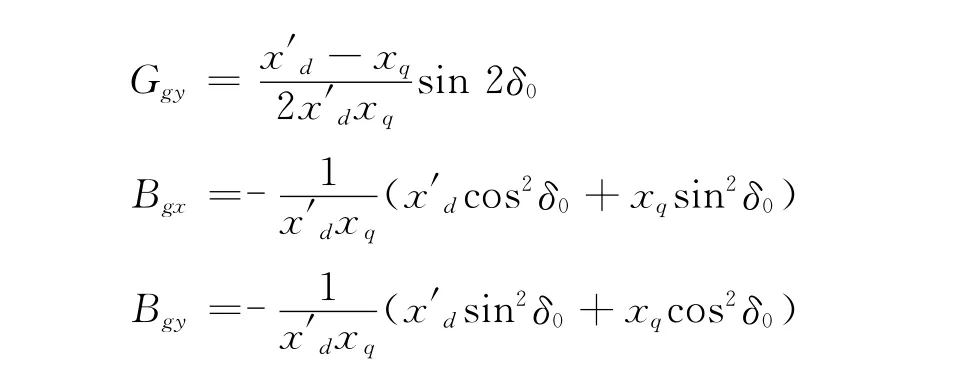
式 中:aδ= Ggxcosδ - Bgxsinδ;bδ= Bgycosδ +Ggysinδ;aq= E′q[(G′gx- Bgx)cosδ - (Ggx+B′gx)sinδ]-(G′gxVx0-B′gxVy0);bq=E′q[(G′gy-Bgy)cosδ + (Ggy- B′gy)sinδ]- (G′gyVy0+B′gyVx0);G′gx、G′gy、B′gx、B′gy分 别 为 Ggx、Bgx、Bgy、Ggy对转子角δ的导数;ΔIgx、ΔIgy为发电机节点的机端电流相量在直角坐标系下的x轴、y轴分量的增量。
直流输电系统的动态特性主要受直流控制方式的影响,本文以整流侧定电流-逆变侧定触发角为例,计及直流功率调制环节,则直流输电系统线性化后的动态方程为
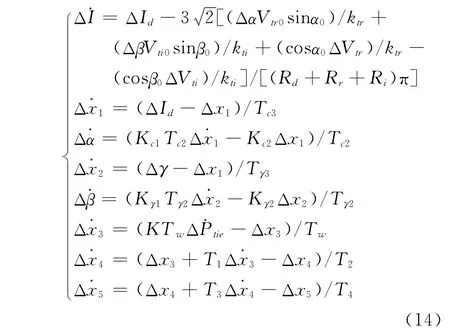
式中:Vtr0、Vti0分别为直流整流侧、逆变侧空载直流电压;ktr、kti分别为整流侧、逆变侧换流变压器变比;ΔVtr、ΔVti分别为整流侧、逆变侧实际电压的增量;ΔPtie为与直流系统并联的交流联络线有功功率变化量;Δx1、Δx2、Δx3、Δx4、Δx5为中间变量。
直角坐标系下直流输电系统的代数方程:
一杭独自坐在母亲的坟前,小心地展开那份发脆的剪报,一篇题为《爸爸,我知道您会回来》的散文,勾起往事。文章是一杭读小学六年级时写的,后来在区报上发表,作家梦也由此播下。

式中:Vt、Vtx、Vty分别为直流换流母线的电压及直角坐标系下的x 轴、y轴 分量;It、Itx、Ity分别 为直流系统注入到交流系统的电流及直角坐标系下的x轴、y轴分量。
不计换流站有功损耗,换流站注入到系统的有功功率为
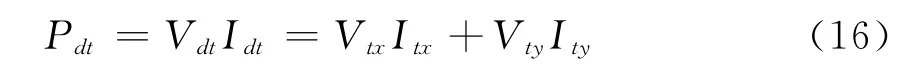
结合式(15)、(16)及文献[11],线性化后的直流系统代数方程为

综合式(11)、(12)、(13)、(14)及(17),交直流混合系统的线性化微分代数方程为

式中:B= [Ygg-Dg,Ygd,Ygt;Ydg,Ydd-Dd,Ydl;Ylg,Yld,Yll]T;Δxg= [Δδ,Δω,ΔE′q,ΔEfd]T;Δxd=[ΔId,Δx1,Δα,Δx2,Δβ,Δx3,Δx4,Δx5]T;Δδ、Δω、ΔE′q、ΔEfd为 发 电 机 的 状 态 向 量;ΔId、Δx1、Δα、Δx2、Δβ、Δx3、Δx4、Δx5为直流系统的状态变量;ΔVg、ΔVt、ΔVl分别为机端、换流母线、负荷节点的电压向量。
消去式(18)中ΔVg、ΔVt、ΔVl可得出对应的交直流系统状态方程为

式中
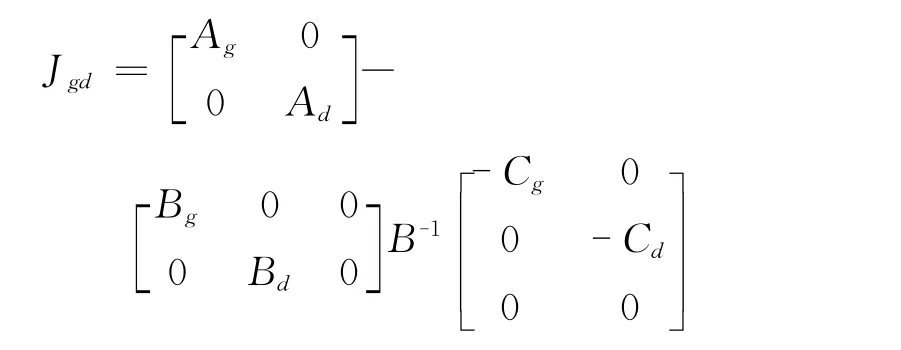
4 模态分析方法

式中,λ为Jgd的特征值集合,λ= [λ1,λ2,…,λn],n为Jgd的维数;单位阵I与Jgd同维。
利用QR法、SMA法等求式(20)的特征值,再根据求得的特征值判断系统稳定性:
(1)一个实特征值对应一个非振荡模式。负特征值代表衰减模式,其绝对值越大,系统越容易稳定;正实特征值表明系统将出现非周期失稳。
(2)复特征值以共轭对形式出现,即

式(21)对应系统的一个振荡模式,σ刻画了系统对振荡模式的阻尼能力,ω为振荡模式的有阻尼振荡频率。其振荡模式下的无阻尼振荡频率f为

对应的振荡模式的阻尼比ζ为:

通常将振荡频率为0.1~2.5Hz的振荡模式定为电力系统低频振荡模式。振荡频率介于0.1~0.7Hz为区域间振荡模式;振荡频率介于0.7~2.5Hz为本地振荡模式。某一振荡模式下,若ζ>0.05,则系统阻尼强,该模式下系统动态稳定;若0.03<ζ<0.05,则系统阻尼比较弱,该模式下系统动态稳定性较弱,需采取措施改善该模式下的系统动态稳定性;若ζ<0.03,则系统弱阻尼或负阻尼,必须采取措施改善系统的动态稳定性。
5 直流调制环节参数整定
根据所建立的交直流混合系统动态方程及模态分析方法,求解式(19)中状态矩阵的特征值,计算区域间振荡频率的阻尼比,若区域间振荡处于弱阻尼或负阻尼时,宜采用直流调制的方式提高区域间振荡阻尼比,改善系统的动态稳定性[6,7]。
直流调制的控制策略通常基于根轨迹法[14],未加入直流调制的闭环控制系统具有一对主导共轭极点,区域间低频振荡的响应特性主要由这一对主导共轭极点的位置决定。当系统区域间低频振荡的响应特性不满足要求时,通常将对系统性能指标的要求化为决定期望主导极点的位置。引入直流调制环节,借助直流调制环节的零极点改变原系统根轨迹,使交直流混合系统的根轨迹通过期望主导极点或通过期望主导极点的邻域,从而改善整个系统区域间低频振荡的阻尼特性。
直流调制通常以直流输电系统的功率增量ΔPdc作为控制变量和交流联络系统有功功率增量ΔPac作为被控制变量,并将ΔPac作为反馈输入,系统闭环传递函数框图如图3所示。系统传递函数为
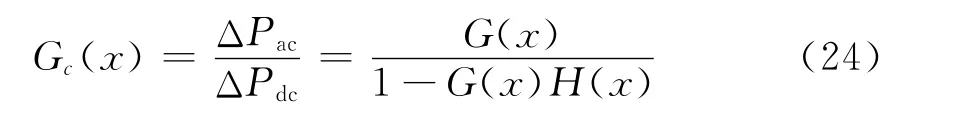
对应闭环系统特征方程为

加入反馈环节H(x)后,闭环系统的主导极点为s*,则s*必满足如下条件:
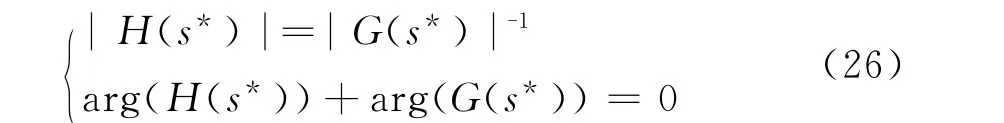
由式(26)便可计算直流调制环节H(x)所需补偿的相位和增益,根据图3可知调制环节利用了2级超前滞后补偿环节。每级补偿arg(H(s*))/2,由超前环节基本公式可知式(7)中参数α、T分别为
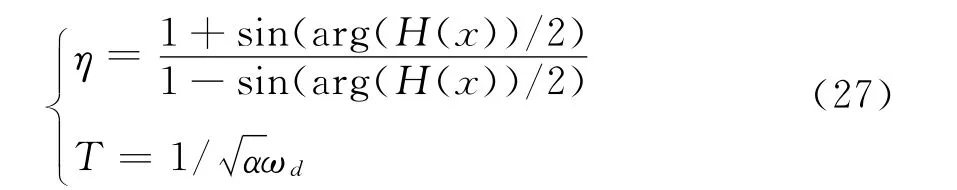
根据直流调制环节即为图3中的闭环反馈环节,其对应的传递函数为H(x)。由式(26)即可计算出式(7)的增益K:
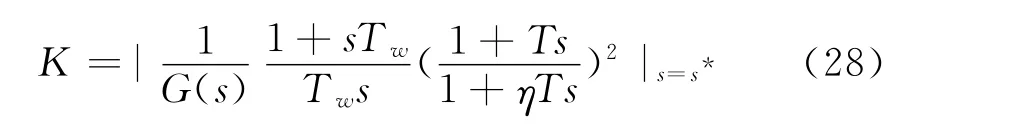
将η、T、K代入式(7)即可得出图2所示的直流附加功率调制环节的各项参数。
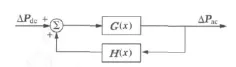
图3 闭环控制系统框图Fig.3 Block diagram of closed-loop control system
6 仿真分析
本文在PSSE中构建了含标准直流系统的交直流系统算例模型,直流系统参数详见文献[15],交流系统参数见文献[16]。算例模型中,在母线7与12之间加装了一台230kV/345kV的变压器,并将直流输电系统降低传输容量运行。另外,模型分别在直流输电系统两侧的整流、逆变侧的换流母线上装设容量为2×150Mvar和2×125Mvar的高压电抗器,以平衡标准直流系统由于滤波和小负荷运行而引起的无功功率过剩问题,同时保证算例直流所联交流系统与原模型中直流换流站所连交流系统短路比相同。
为详细分析直流调制对系统动态稳定性的影响,分别在直流传输容量为100MW和200MW时,设置6种场景:Scenario-1和Scenario-4,为无联络线停运;Scenario-2和Scenario-5为母线8、9间支路1停运;Scenario-3和Scenario-6为母线8、9及7、8间支路1停运。借助于模态分析方法计算上述6种场景下的系统静态稳定性。直流系统的传输容量为100MW、200MW时,计算的直流系统无功率调制时区域间振荡频率及阻尼比见表1。
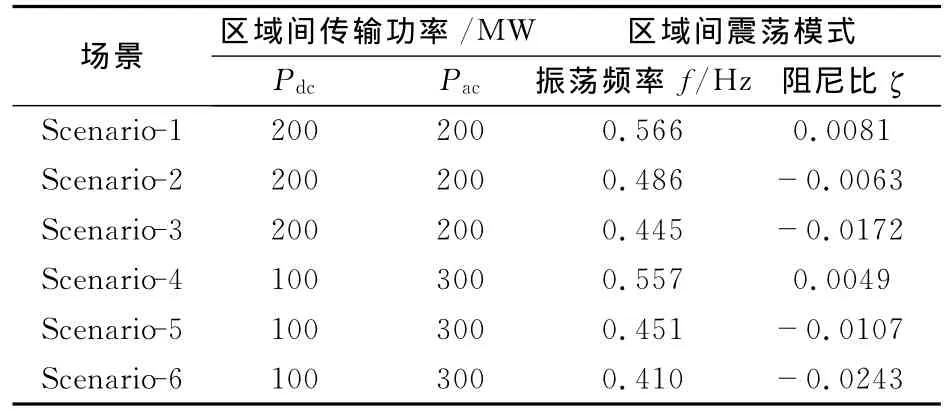
表1 无直流调制的区域间振荡频率及阻尼比Tab.1 Frequency and damping ratio of interarea mode without HVDC modulation
由表1的结果可知,在上述6种场景下系统区域间振荡频率为0.410~0.566Hz,阻尼比为-0.0243~0.0081,系统在该区域间振荡模式下处于负阻尼状态,动态稳定性弱,必须采取措施改善系统的动态稳定性。考虑到在交直流系统中,可采用直流调制改善系统的动态稳定性,加入直流调制后,期望的区域间振荡频率及阻尼比选择为0.5 Hz、0.25即期望决定区域间机电振荡响应特性的闭环控制系统主导极点为:-0.785±j3.05。将该主导极点代入式(25)中的G(s)中,求得的各场景下开环传递函数的幅值及相位见表2。
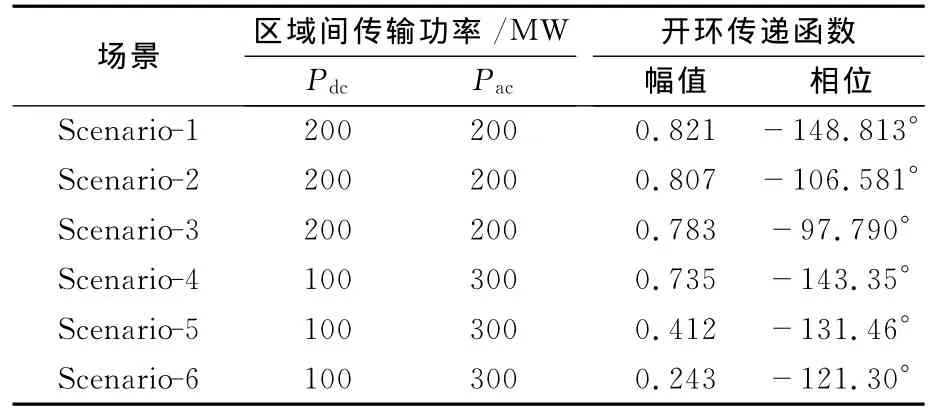
表2 直流调制的区域间振荡幅值及相位Tab.2 Frequency and damping ratio of interarea mode with HVDC supplementary control
由表2可知:arg(G(-0.785±j3.05))的取值范围为-97°~148°,|G(-0.785±j3.05)|的取值为0.243~0.821。由式(26)即可计算采用直流调制构成闭环控制系统的反馈环节(直流调制环节)的参数,本文综合考虑选择反馈环节补偿相位arg(H(-0.785±j3.05))为120°,|H(-0.785±j3.05)|为2。选择隔直环节时间常数Tw为10s,再结合式(27)可求出η、T、K分别为13.93、0.0878、1.3456。因此,式(7)所示的直流功率调制环节传递函数中各参数分别为:K=1.3456,Tw=10,T1=T3=1.2231,T2=T4=0.0878。
根据上述直流功率调制环节参数整定值,计算的区域间振荡频率及阻尼比见表3。对比表2、3可知:在交直流混合输电系统中,采用直流功率调制可显著改善系统区域间动态稳定性。
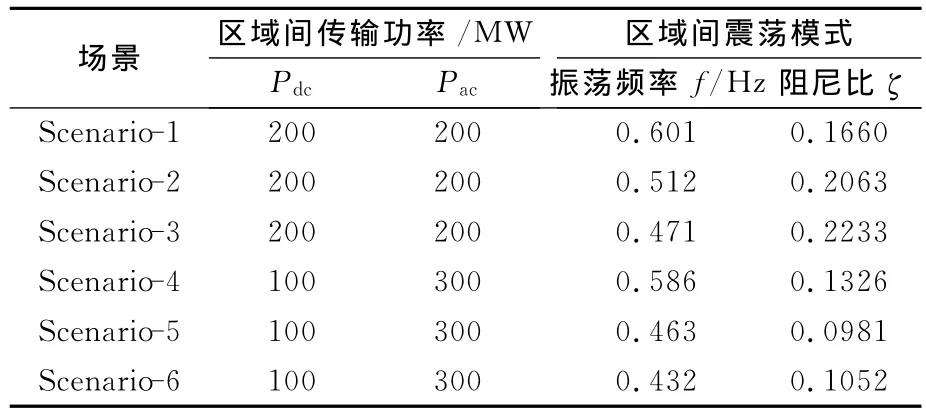
表3 直流调制后的区域间振荡频率及阻尼比Tab.3 Frequency and damping ratio of interarea mode with HVDC modulation
为进一步验证直流调制对改善交直流混合系统暂态稳定性的效果,分别在直流传输容量为100 MW和200MW条件下,设置了两种扰动:扰动1,母线9三相短路,0.1s故障消失;扰动2,无故障跳开母线8、9间的支路1。仿真结果见图4~7。
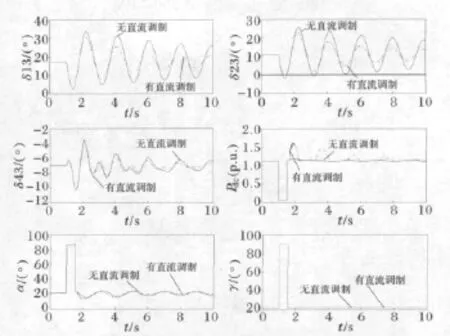
图4 直流传输容量为100MW时扰动1的仿真结果Fig.4 Simulation results of disturbance 1with HVDC transfer capacity of 100MW
结果表明,直流系统采用功率调制环节后,可显著改善系统的暂态稳定性,同时在交直流联络线传输总容量为400MW不变的条件下,直流系统稳态传输容量越大,扰动后直流调制效果越明显。
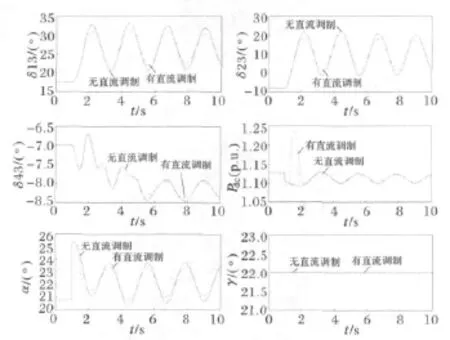
图5 直流传输容量为100MW时扰动2仿真结果Fig.5 Simulation results of disturbance 2with HVDC transfer capacity of 100MW
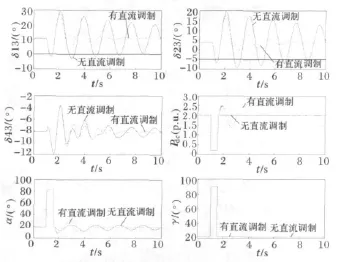
图6 直流传输容量为200MW时扰动1仿真结果Fig.6 Simulation results of disturbance 1with HVDC transfer capacity of 200MW
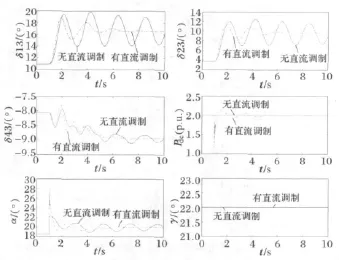
图7 直流传输容量为200MW时扰动2仿真结果Fig.7 Simulation results of disturbance 2with HVDC transfer capacity of 200MW
7 结论
(1)本文计及直流功率调制环节推导直流输电系统动态方程及所搭建的含标准直流模型的典型交直流混合系统模型正确、合理,对工程实际有一定的借鉴意义。
(2)采用直流功率调制可有效抑制区域间低频振荡,且直流传输容量占整个交直流联络线传输容量比重越大,调制效果越明显。
(3)直流系统对电力系统动态稳定性的影响与直流系统控制方式和是否采用功率调制环节紧密相关,合理的直流控制方式及调制策略可有效改善系统的动态稳定性。
[1] 赵婉君.高压直流输电工程技术[M].北京:中国电力出版社,2004.
[2] Vovos N A,Galanos G D.Enhancement of the transient stability of integrated AC/DC systems using active and reactive power modulation[J].IEEE Trans on Apparatus and Systems,1985,104(7):1696-1702.
[3] Taylor C W,Lefebvre S.HVDC controls for system dynamic performance[J].IEEE Trans on Power Systems,1991,6(2):743-752.
[4] Klein M,Rogers G J,Kunder P.A fundamental study of inter-area oscillations in pswer System[J].IEEE Trans on Power Systems,1991,6(3):914-921.
[5] 陈文滨,张尧,谢惠藩(Chen Wenbin,Zhang Yao,Xie Huifan).UHVDC故障下紧急直流功率支援方案研究(Study on emergency DC power support for UHVDC fault)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2010,22(6):113-118.
[6] 陈虎,贺洋,张英敏,等(Chen Hu,He Yang,Zhang Yingmin,etal).四川电网多送出直流输电系统交互 影 响 分 析 (Interaction analysis of multi-send HVDC systems of Sichuan power grid)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2011,23(4):21-26.
[7] Hammad A E.Stability and control of HVDC and AC transmission in parallel[J].IEEE Trans on Power Delivery,1999,14(4):1545-1554.
[8] 宗秀红,张尧,武志刚(Zong Xiuhong,Zhang Yao,Wu Zhigang).交直流混合系统低频振荡的概率特征根分析(Probabilistic Eigenvalue analysis for low frequency oscillation of AC/DC parallel systems)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2006,18(6):13-17.
[9] 杨卫东,薛禹胜,荆勇,等(Yang Weidong,Xue Yusheng,Jing Yong,et al).直流系统的控制策略对南方电网暂态稳定性的影响 (Influence of DC system's control strategy on the transient stability of south China power grid)[J].电力系统自动化 (Automation of Electric Power Systems),2003,27(18):57-60.
[10] 罗 隆 福, 雷 园 园, 李 勇,等 (Luo Longfu,Lei Yuanyuan,Li Yong,et al).定熄弧角控制器对直流输电系统的影响分析(Effects of constant arc extinguishing angle controller on HVDC transmission system)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2009,21(5):97-103.
[11] 李国庆,陈厚合,姜涛,等(Li Guoqing,Chen Houhe,Jiang Tao,et al).基于微分代数模型的直流非线性附加控制(Nonlinear supplementary control for HVDC based on differential-algebraic model)[J].电力自动化设备(Electric Power Automation Equipment),2011,31(6):34-38.
[12] 陈厚合,李国庆,姜涛(Chen Houhe,Li Guoqing,Jiang Tao).控制方式转换策略下的改进交直流系统潮流算法(A modified power flow algorithm for AC/DC power system under transformation strategy of converter control modes)[J].电网技术(Power System Technology),2011,35(8):93-98.
[13] Moussa H A M,Yao-nan Yu.Dynamic interaction of multi-machine power system and excitation control[J].IEEE Trans on Power Apparatus and Systems,1974,93(4):1150-1158.
[14]刘取.电力系统稳定性及发电机励磁控制[M].北京:中国电力出版社,2007.
[15]Szechtman M,Wess T,Thio C V.A benchmark model for HVDC control studies[C]∥AC and DC Power Transmission Conference,Landon,UK:1991.
[16]Kunder P.Power System Stability and Control[M].New York:McGraw-Hill,1994.

