并联型有源电力滤波器的延时补偿控制

王晓刚，谢运祥，王 清，张 杰

（1.广州大学机械与电气工程学院，广州510006；2.华南理工大学电力学院，广州510641）

并联型有源电力滤波器APF（active power filter）是补偿电流型谐波、无功功率、提高电能质量的有效手段［1］。APF的控制系统可以在连续域（s域）和离散域（z域）下进行设计。其中最为经典的是PI控制，其思路是首先建立APF在同步旋转坐标系下的模型并进行解耦，然后对d轴系统和q轴系统分别应用PI控制［2，3］。但单一的PI控制难以同时获得理想的稳态和暂态性能，对此，文献［4～8］提出了多种改进策略或PI参数优化设计方法，但大多数方法均在s域设计或没有考虑数字化控制的影响。实际上，s域下设计的控制器用数字方法直接实现时系统的稳定域要缩小，而且由于计算和采样等原因造成的延时，数字控制多采用差一拍控制，使稳定范围进一步缩小。重复控制是一种新型的数字控制方法，它基于内模原理，能有效消除静差，重复控制器可单独使用，也可与其它方法一起构成复合控制系统，逆变电源是重复控制的典型应用［9～11］，APF是它的最新应用场合［12～15］。

本文建立了APF的离散模型，对差一拍控制对基于数字PI控制APF的影响做出分析，指出延时会使比例系数和积分系数的选取范围严重缩小，从而影响着控制的性能。在此基础上，提出将比例控制与重复控制相结合的APF电流差一拍控制策略，其中比例控制保证系统具有一定的快速性，重复控制嵌入在电流误差和比例控制之间，对电流跟踪误差进行校正，代替了PI控制中的积分环节，有效地补偿了延时的影响。为验证所提控制策略的正确性，进行仿真研究，结果表明补偿后的电网电流为十分理想的正弦波，暂态性能较理想，有效补偿了差一拍控制的影响。

1 有源电力滤波器系统模型

并联型APF主电路如图1所示。图中，us为公共连接点PCC（point of public connection）处的电压，L为交流侧接口电感，R是电感的电阻，Cdc是直流侧电容，udc是直流侧电压。ic为APF输出的补偿电流，is网侧电流，iL为负载侧电流，uc为逆变器输出电压。

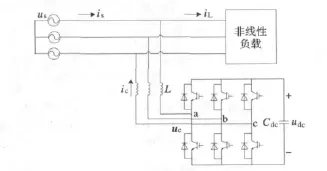
图1 有源电力滤波器主电路Fig.1 Main circuit of the active power filter

APF交流侧部分在同步选择坐标系下的模型为

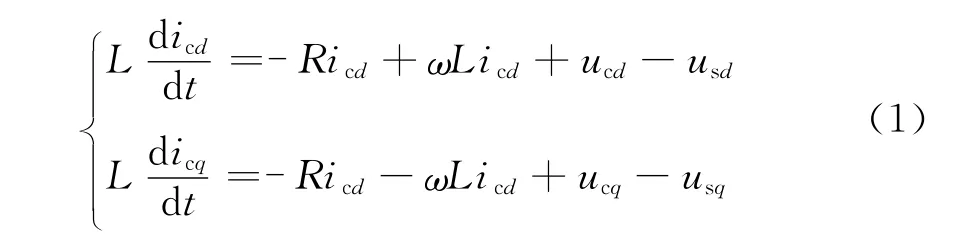
对式（1）进行离散化处理，得

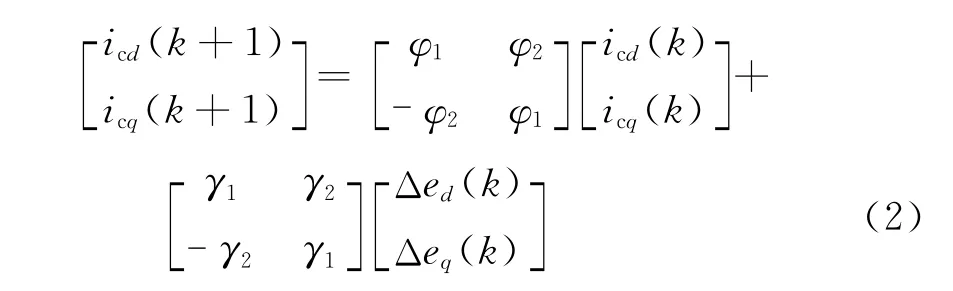
其中Δed（k）＝ucd（k）－usd（k），Δeq（k）＝ucq（k）－usq（k）。忽略零阶保持器的影响，式（2）中的矩阵元素为

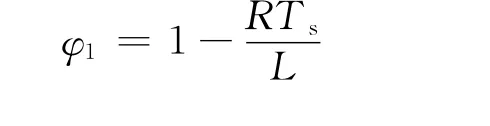
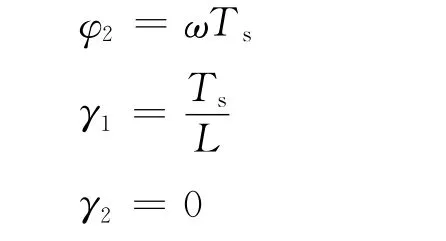
其中Ts是采样周期，也是开关周期。从式（2）中容易看出，系统在d轴和q轴间存在耦合，为了解耦，定义ud和uq为

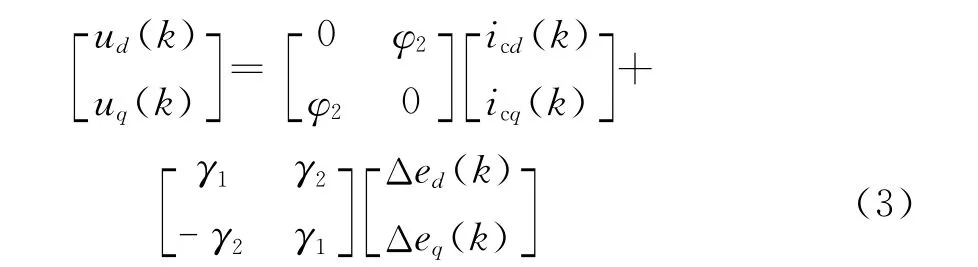
则式（2）可以写为

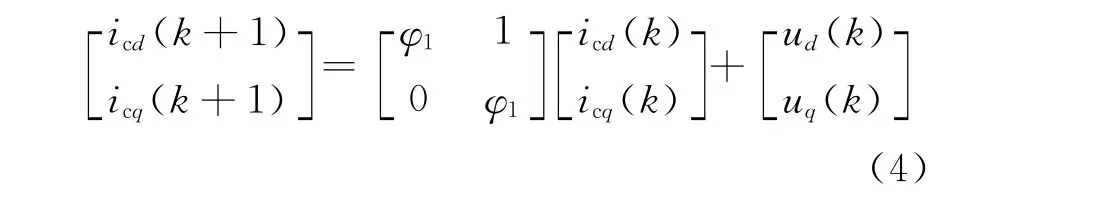
上式实现了系统的解耦，可以对d轴和q轴系统进行独立控制。

2 数字PI控制及其受差一拍控制的影响

若采用数字PI控制，则控制系统的结构图如图2所示，其中、为d轴和q轴电流指令值，icd、icq为d轴和q轴电流实测值，kp、ki为比例系数和积分系数，ud和uq为解耦部分的输出，usd和usq为PCC电压，ucd和ucq为控制器输出的控制量。

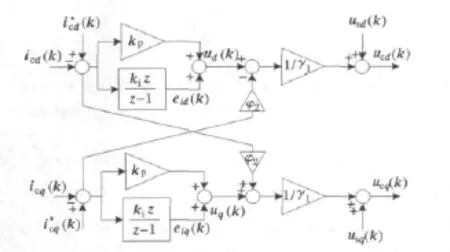
图2 APF的PI解耦控制Fig.2 PI decoupling control for the APF

以d轴为例，解耦部分输出的ud（k）为

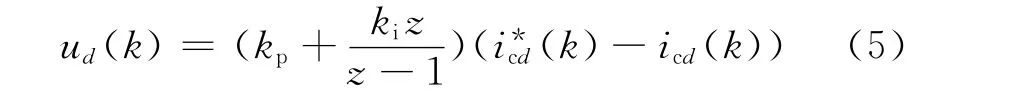
其中kp、ki分别为比例系数和积分系数。定义eid为PI控制器积分项的输出，即：

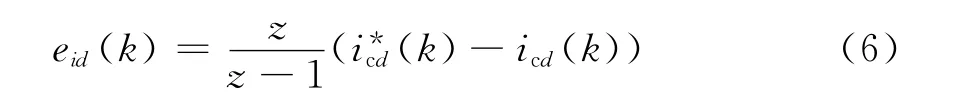
进一步变为：

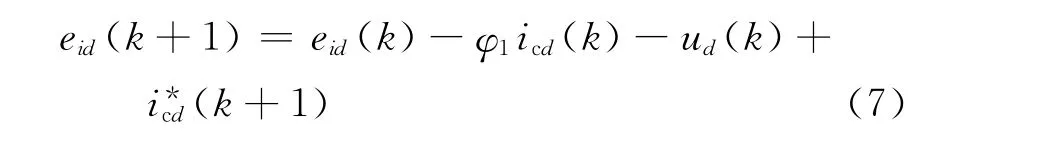
将eid作为一个新的状态变量，与icd构成的d轴增广状态空间方程为：

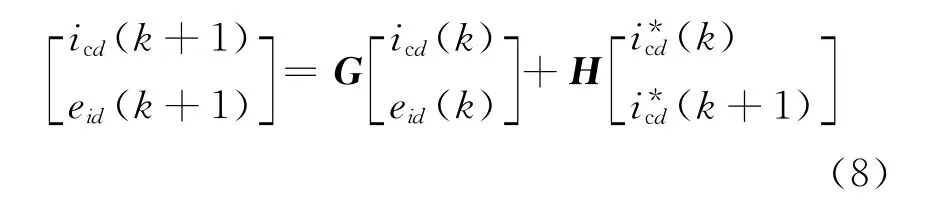
其中

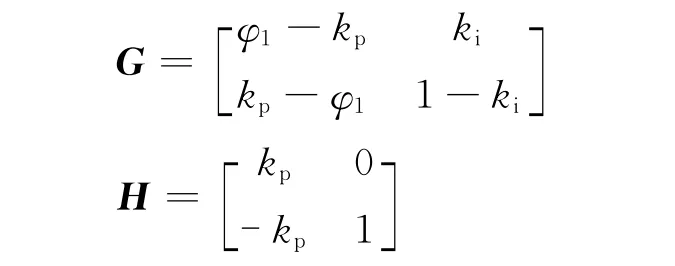
则矩阵G决定了APF的d轴系统的特征方程：

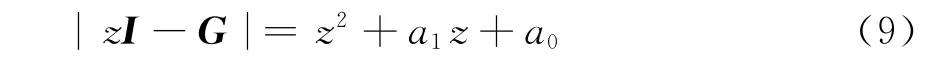
其中a1＝kp＋ki－φ1－1，a0＝φ1－kp。根据Routh判据解得kp和ki需满足的条件为

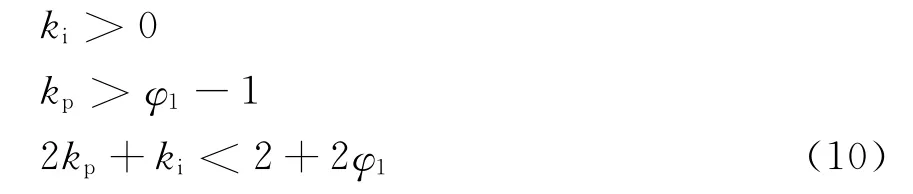
设L＝5mH，R＝0.5Ω，采样周期Ts＝100 μs，计算得φ1＝0.99，此时系统的稳定条件为2kp＋ki＜3.98。以kp为横坐标、ki为纵坐标，则系统稳定范围位于图3所示的直线以下。

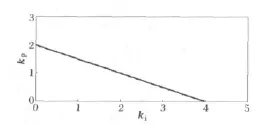
图3 离散PI控制kp与ki的取值范围Fig.3 Range of kpand kiin discrete PI control

为了避免计算和采样等原因造成的延时使PWM脉冲输出宽度减小，常采用差一拍控制，其原理是将k周期计算出的控制量在k＋1周期到来时输出，相当于在控制系统中增加了单位延迟环节z－1。

设新状态变量xp（k）＝icd（k－1），xi（k）＝eid（k－1），则差一拍控制的APFd轴PI控制可用如下离散增广状态方程描述：

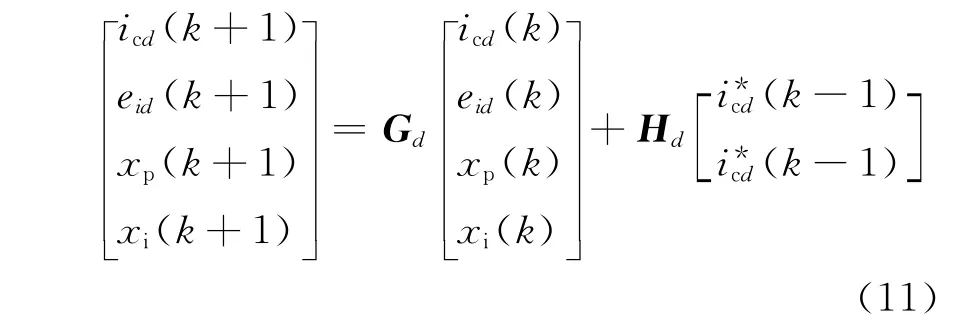
其中

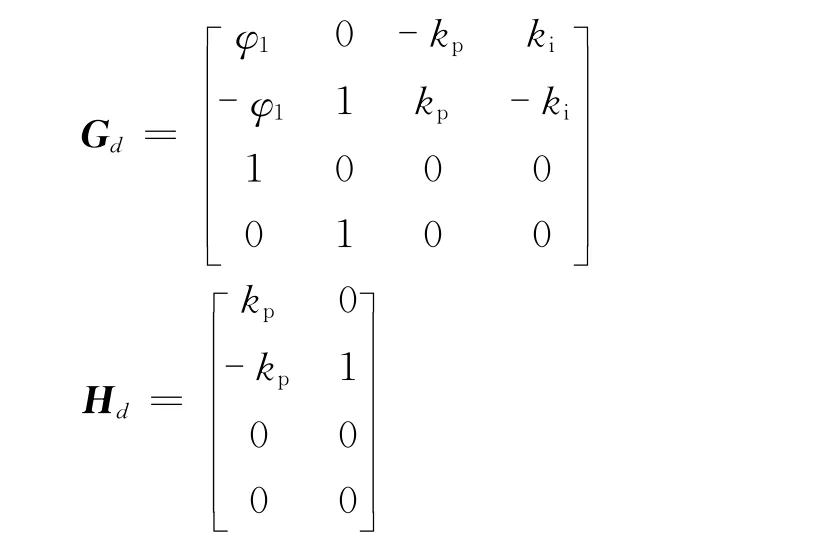
矩阵Gd决定了系统的d轴系统特征方程

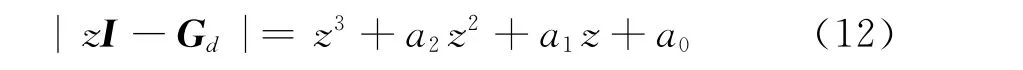
其中a2＝－φ1－1，a1＝φ1＋kp＋ki，a0＝－kp。根据Routh判据解得kp和ki需满足的条件为

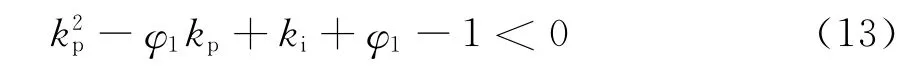
将前面的参数代入式（13）得到系统稳定范围位于图4所示的曲线以左。

比较图3和图4可知，差一拍控制使kp和ki的取值范围大大减小，使PI控制的性能大为降低。

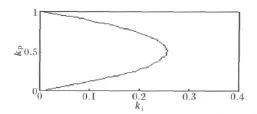
图4 离散延时一周期PI控制kp与ki的取值范围Fig.4 Range of kpand kiin discrete PI control with one period delay

3 比例控制与重复控制结合的APF延时补偿

由于差一拍控制时仅通过调节PI参数已经难以使APF获得理想的补偿能力，稳态时将有较大的误差残留，为此引入重复控制。重复控制基于内模原理，可单独使用，也可与其它控制构成复合控制系统。重复控制与PI控制构成的APF电流控制器（d轴系统，q轴与之相同）如图5所示。其中P（z）为原差一拍PI控制器，虚线方框中为重复控制器，包括滤波器Q（z）、周期延时环节z－N和补偿器C（z），其中C（z）是设计的难点。

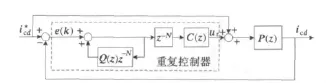
图5 重复控制与PI控制构成的复合控制器Fig.5 Compound controller consists of repetitive control and PI control

P（z）的表达式为

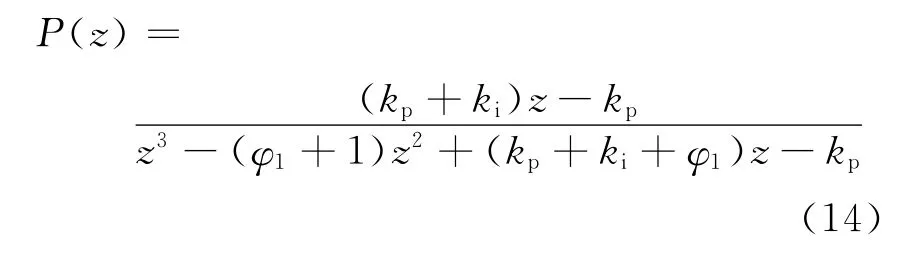
由式（14），APF差一拍PI控制系统P（z）在kp＝0.5且ki分别等于0、0.05、0.1、0.15、0.2时的频率特性如图6所示。可见，P（z）在约7200rad／s的中高频附近均出现了谐振峰值，且ki＝0时谐振峰值最小，ki越大谐振峰值也越大，容易引发谐振，威胁着系统的稳定性；由相频特性可见，频率小于谐振峰值频率时ki越大相位滞后越小，而频率大于谐振峰值频率时正好相反，但总的来说，相位滞后均较大，P（z）的相频特性不理想。

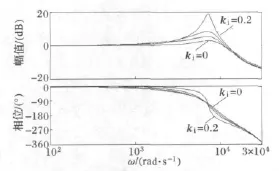
图6 P（z）在ki不同时的频率特性Fig.6 Frequency characteristics of P（z）with different ki

ki越大谐振峰越大，也使补偿器C（z）的设计变得相对困难。但是由于差一拍时ki的可调范围很小，对跟踪精度的改善已经十分有限，而且与重复控制结合后，稳态精度的改善变成重复控制的任务，故将积分环节省略，构成比例＋重复控制的复合控制系统。只有比例控制且kp不同时P（z）的频率特性如图7所示，kp分别取0.1、0.2、0.3、0.4、0.5，可见，kp＝0.5时还有一定的谐振峰，而kp＝0.3时谐振峰已经不存在，但kp越小，低频增益也越低，电流跟踪的快速性不能得到保证，且由相频特性可见，kp越小相位滞后也越大，故kp还是应取得大一些，本文取kp＝0.5。

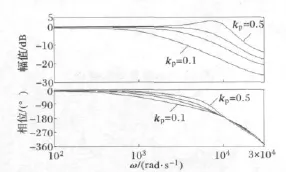
图7 P（z）在ki＝0和kp不同时的频率特性Fig.7 Frequency characteristics of P（z）when ki＝0with different kp

为了抵消P（z）在kp＝0.5时不大的谐振峰，而且在P（z）截止频率附近使幅频特性迅速下降，选取以下形式的零相移陷波器：

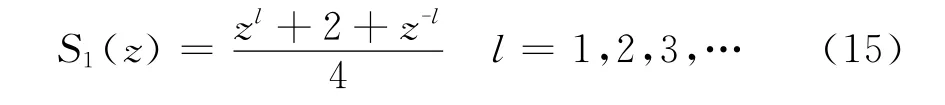
此陷波器的设计目标就是选择l，使陷波点刚好或近似抵消P（z）的谐振峰。经过反复仿真，发现l＝4较为合适，此时陷波点频率约为7750rad／s。P（z）、S1（z）、校正后的系统S1（z）P（z）的频率特性均示于图8，可见S1（z）P（z）的中低频增益保持为0，且在谐振峰附近幅频特性迅速衰减；但是，S1（z）也使中频段的一部分频带的带宽降低，幅频特性在2000rad／s（约318Hz）左右开始出现较明显下降，影响了7次以上谐波的补偿，使补偿效果的改善不明显。而且，在高频段，S1（z）P（z）的幅频特性增益较高，为了降低高频开关噪声或其它噪声的干扰，还需引入低通滤波器S2（z）使高频衰减，增加了控制器的复杂性。

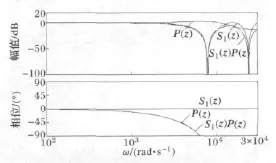
图8 S1（z）对P（z）的校正Fig.8 Correction of P（z）by S1（z）

仔细观察P（z）的幅频特性，发现其谐振峰幅值较低，故仅用一低通滤波器S（z）就可以拉低P（z）的幅频特性，S（z）的截止频率可以选得比谐振峰频率高，如选为8168rad／s（1300Hz），设计出的3阶Butterworth滤波器为

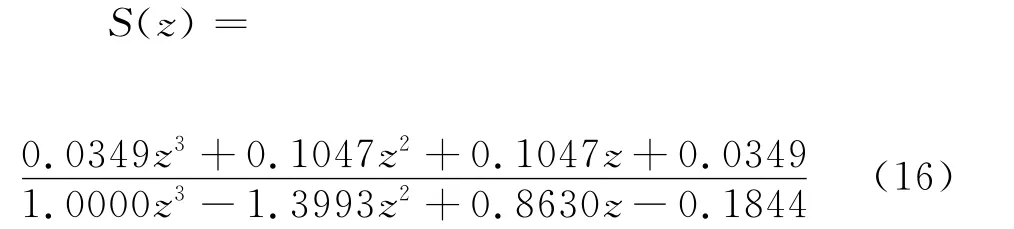
P（z）、S（z）、校正后的系统S（z）P（z）的频率特性均示于图9。由图可见，校正后的系统S（z）P（z）幅频特性在高频段得到了衰减，但是相频特性的滞后也变得更加严重，相角裕度为负值，不能保证系统的相对稳定性。

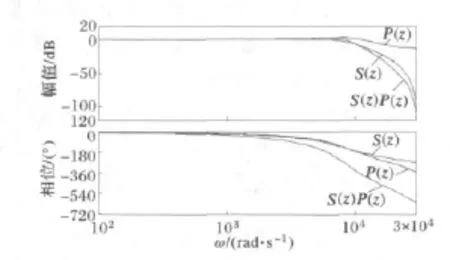
图9 S1（z）对P（z）的校正Fig.9 Correction of P（z）by S1（z）

超前环节zk的作用就是补偿S（z）P（z）的相位滞后。zk的模恒为1，在幅频特性中是一条恒为0的直线，即对幅频特性没有影响；它的相频特性与频率有关，由于zk＝ejkωT，所以它相频特性的曲线呈指数规律增加，正好补偿对象的相位滞后。

APF的采样频率取10kHz，经过反复仿真试验，发现zk＝z5对相位的补偿较为合适，使z5S（z）P（z）的相角裕度（即z5S（z）P（z）的相角加上180°）为正值，保证了系统的相对稳定性。虽然z5在物理上是不可实现的，但由图5，z5与前级的z－N串联后的z－N＋5是完全可以实现的。校正的效果如图10所示。

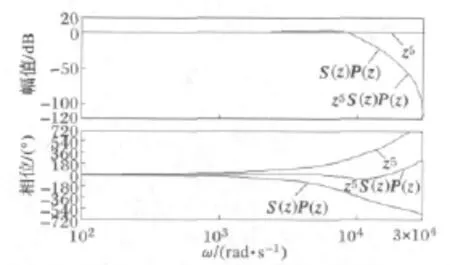
图10 z5 对S（z）P（z）的相位校正Fig.10 Phase correction of S（z）P（z）by z5

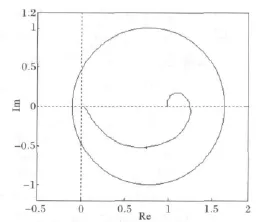
图11 krej kωTS（ejωT）P（ejωT）的奈氏曲线Fig.11 Nyquist plot of krej kωTS（ejωT ）P（ejωT ）

补偿器C（z）最后一个需要设计的环节是重复控制增益kr，kr在0到1之间取值，一般先将kr设为1，先进行zk和S（z）的设计，保证zkS（z）P（z）的稳定性，最后再调整kr，减小kr可以使矢量krejkωTS（ejωT）P（ejωT）的幅值减小，提高系统的鲁棒性，但是过小的kr也使重复控制的响应变慢，故一般取一比1稍小的数，本文取为0.95。

krejkωTS（ejωT）P（ejωT）奈氏图绘于图11中，低频从（1，0）开始，高频止于零点，可见在全频段内，krejkωTS（ejωT）P（ejωT）都在单位圆内，离边界具有一定的距离，具有足够的稳定裕量。

4 仿真研究

为了验证算法的有效性，在 Matlab／Simulink环境中建立了基于上述比例控制与重复控制结合的APF系统模型；仿真中使用的参数为：电网相电压有效值220V；非线性负载为二极管整流桥带阻感负载；接口电感L＝5mH，R＝0.5Ω，直流侧电容Cdc＝4700μF，直流电压Udc＝800V，开关频率fs＝10kHz，采用空间矢量脉宽调制。

图12为非线性负载电流，其含有大量谐波，幅值约30A，基波幅值为26A。图13为无延时情况下数字PI控制在kp＝1、ki＝1时的补偿结果，因kp和ki值在图3的稳定范围内，所以系统稳定，补偿效果良好，电网电流THD%＝2.4%。图14为差一拍控制的数字PI控制在kp＝0.5、ki＝0.3时的补偿结果，因kp和ki的值超出图4的稳定范围，所以系统不稳定。减小ki，使其等于0.1，则取值位于图4的稳定范围内，系统稳定，但kp和ki取值过小，补偿效果较差，电网电流THD%＝9.9%。

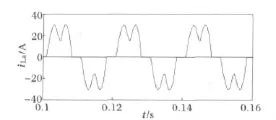
图12 非线性负载电流Fig.12 Nonlinear loads current

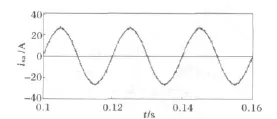
图13 PI控制在无延时、kp＝1、ki＝1时的电网电流Fig.13 Grid current when PI controller（kp ＝1，ki＝1）without delay is applied

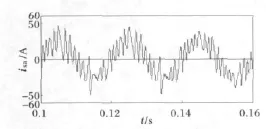
图14 PI控制在差一拍、kp＝0.5、ki＝0.3时的电网电流Fig.14 Grid current when PI controller（kp ＝0.5，ki＝0.3）with one period delay is applied

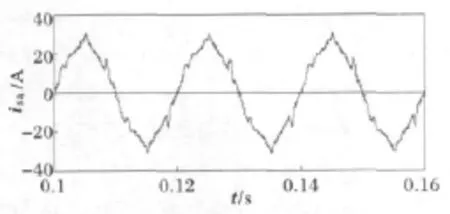
图15 PI控制在差一拍、kp＝0.5、ki＝0.1时的电网电流Fig.15 Grid current when PI controller（kp ＝0.5，ki＝0.1）with one period delay is applied

图16为采用本文提出的比例控制与重复控制结合的差一拍控制方法补偿结果，可见APF输出电流跟踪指令电流迅速，误差小，电网电流为十分理想的正弦波，幅值约为26A，THD% ＝1.8%，与无延时数字PI控制时相比更小。图17为本文方法的暂态性能，非线性负载在0.13s发生突变，由于重复控制的延时特性，电网电流在约一个周波后恢复为理想正弦，同时因为比例控制的作用，暂态过程中电网电流仍能保证一定的正弦度。

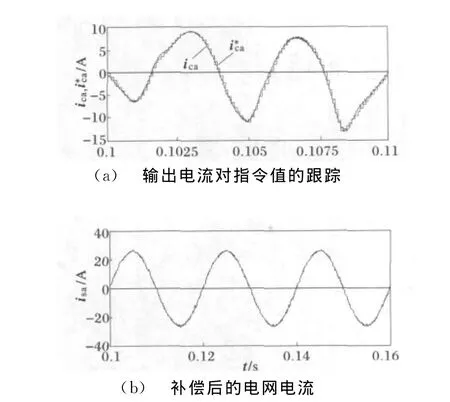
图16 采用复合控制时的补偿结果Fig.16 Harmonic compensation results when the compound control is applied

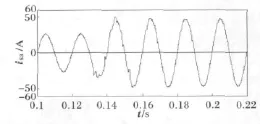
图17 负载变化时复合控制的补偿结果Fig.17 Harmonic compensation results when the compound control is applied

5 结语

常规的APF PI解耦控制方法在数字化后受延时的影响较大。为了消除延时的影响，本文提出一种比例控制和重复控制结合的有源电力滤波器差一拍电流控制策略。仿真结果表明该策略使有源电力滤波器在控制量延时一个控制周期输出时仍能实现高性能的谐波补偿，系统动静态性能优良，具有较强的实用价值。

［1］ 张颖（Zhang Ying）.有源滤波器在改善电能质量中的应用（Application of active power filter to improve power quality）［J］.电力系统及其自动化学报（Proceedings of the CSU－EPSA），2010，22（4）：103－106.

［2］ Mikkili S，Panda A K，Patnaik S S，etal.Comparison of two compensation control strategies for SHAF in 3ph 4wire system by using PI controller［C］／／India International Conference on Power Electronics，New Deihi，India：2011.

［3］ Xueliang Wei，Kai Zhao，Kai Shuang.Current control strategy research for active power filter［C］∥IEEE EUROCON，St.－Petersburg，Russia：2009.

［4］ 胡凯，申群太（Hu Kai，Shen Quntai）.基于微粒群算法优化PI参数的单相有源电力滤波器（Single－phase active power filter based on particle swarm optimized PI regulator）［J］.电力系统保护与控制（Power System Protection and Control），2009，37（18）：51－56.

［5］ Etxeberria－Otadui I，de Heredia A L，Gaztanaga H，etal.A single synchronous frame hybrid（SSFH）multifrequency controller for power active filters［J］.IEEE Trans on Industrial Electronics，2006，53（5）：1640－1648.

［6］ 郭文杰，林飞，郑琼林（Guo Wenjie，Lin Fei，Zheng Qionglin）.三相电压型PWM整流器的级联式非线性PI控制（The cascaded nonlinear PI control for three－phase voltage source PWM rectifier）［J］.中国电机工程学报（Proceedings of the CSEE），2006，26（2）：138－142.

［7］ 吴勇（Wu Yong）.有源电力滤波器电流控制PI校正研究（Research of PI current control of active power filter）［J］.变频器世界（The World of Inverters），2008，（7）：92－95.

［8］ 周柯，罗安，唐杰（Zhou Ke，Luo An，Tang Jie）.基于PI迭代学习的有源滤波器电流跟踪控制（PI iterative learning for current－tracking control of active power filter）［J］.电力电子技术（Power Electronics），2006，40（4）：53－55.

［9］ 刘新民，邹旭东，康勇，等（Liu Xinmin，Zou Xudong，Kang Yong，et al）.带状态观测器的逆变器增广状态反馈控制和重复控制（An inverter based on statefeedback integral control and repetitive control technology with state－observer）［J］. 电 工 技 术 学 报（Transactions of China Electrotechnical Society），2007，22（1）：91－95.

［10］ 熊健，史鹏 飞，张凯，等（Xiong Jian，Shi Pengfei，Zhang Kai，et al）.基于积分环节电压微分反馈的逆变器重复控制策略（Voltage－differential－feedback with integral control plus repetitive control for PWM inverters）［J］.电工技术学报（Transactions of China Electrotechnical Society），2007，22（1）：85－90.

［11］ 杨金辉，戴瑜兴，易龙强，等（Yang Jinhui，Dai Yuxing，Yi Longqiang，et al）.基于重复控制原理的正弦逆变控制（Sine inverter control based on repetitive control arithmetic）［J］.电力电子技术（Power Elec－tronics），2010，44（5）：65－66，72.

［12］ Wei Xueliang.Shunt APF based on current loop repetitive control［J］.Journal of Convergence Information Technology，2010，5（4）：29－37.

［13］ Mattavelli P，l Marafao F P.Repetitive－based control for selective harmonic compensation in active power filters［J］.IEEE Trans on Industrial Electronics，2004，51（5）：1018－1024.

［14］ 耿攀，戴珂，魏学良，等（Geng Pan，Dai Ke，Wei Xueliang，et al）.三相并联型有源电力滤波器电流重复控制（The repetitive control algorithm based current waveform correction for shunt active power filter）［J］.电工技术学报（Transactions of China Electrotechnical Society），2007，22（2）：127－131.

［15］ 武健，何娜，徐殿国（Wu Jian，He Na，Xu Dianguo）.重复控制在并联有源滤波器中的应用（Application of repetitive control technique in shunt active power filter）［J］.中国电机工程学报（Proceedings of the CSEE），2008，28（18）：66－72.